
2025年8月9日
このテキストの目的は,保健・医療分野において,主として学位論文取得を目指す大学院生を対象に,どのように研究計画をデザインし,どのように実験や調査によって生データを得て,どのようにデータファイルを作成し,どのようにデータの性質を確認し,どのように統計解析を進め,その結果を解釈して論文にまとめるか,という一連の流れのガイドラインを示すことである。神戸大学大学院保健学研究科で2012年度から担当している『エビデンスベーストヘルスケア特講』(2019年度から『保健学研究共通特講IV, VIII』)のテキストとして開発した。
なお,このテキストで統計解析において用いるソフトウェアは,2003年にピアソン・エデュケーションから『Rによる統計解析の基礎』を出版した頃から考えると信じられないほど普及しているRと,Rの代表的なGUIフロントエンドであるRcmdrを医療統計向けに自治医科大学の神田善伸先生がフルカスタマイズされたEZRである(一部他のソフトも紹介する)。
問い合わせ先:神戸大学大学院保健学研究科パブリックヘルス領域・教授 中澤 港
e-mail: minato-nakazawa@people.kobe-u.ac.jp
改版履歴
研究成果を学問として発表するためには,2つの本質的条件を満たす必要がある。第1に,これまで誰も発表したことがない,新しい発見を含んでいることである。第2に,既存の学問体系の中で,その研究を位置づけることである。誰も言ったことがないことであっても,既存の学問体系の中に位置づけることができないと,エッセイ(あるいは小説)に過ぎず,学問にはならない。どんな研究でも先行研究をレビューすることが必要なのは,このためである。研究者倫理については、日本学術振興会が発表している文書が参考になるので、どのような分野の研究者であっても読んでおくべきである。
また,人を研究対象とする場合は,倫理的な問題がつきまとうため,事前に所属機関の倫理審査委員会1に研究計画書などを提出し,審査を受けて,その研究に倫理的な問題がないことを保証してもらう必要がある。本学保健学研究科では,詳細はhttp://www.ams.kobe-u.ac.jp/for_staff/rinri/を参照されたい(ただしこのページは学内からしか見えない)。2023年4月8日現在,国の倫理指針の最終改訂は,http://www.mhlw.go.jp/stf/seisakunitsuite/bunya/hokabunya/kenkyujigyou/i-kenkyu/から見ることができる。2023年3月27日付けで人を対象とする生命科学・医学系研究に関する倫理指針(ただし,2022年6月6日付けで1つ前の版のガイダンスも出ていて,こちらの方が読みやすい)が出ている。
長い歴史から,保健医療分野に限らず,研究の進め方には一定のスタイルが確立している。どんなテーマであれ,大きく分けると,2つの型のどちらかに含まれるだろう。
研究を大別すると,問題発見型と問題解決型に分けられる(もちろん,別の分け方もあるだろうが)。
問題発見型の研究は,そのターゲットに対する研究の初期段階で行われる。例えば,パイロットスタディ,ケースレポート,記述調査,問題の定式化のための研究は,この型をとる。
それに対して,問題解決型の研究は,ある程度の研究の蓄積により,問題の所在が明確になった後で行われる。通常は標本調査で,検出力分析を用いたサンプルサイズの設計を含む適切な研究デザインが本質的に重要である。多くの場合,仮説が明確であり,サンプリング→データ→図示→区間推定や検定→有意差や相関の検出(*),モデルの当てはめというプロセスによって仮説検証を行う。
(*) 統計的有意性とP値に関するASA 声明(原文は、"The ASA Statement on p-Values: Context, Process, and Purpose"に含まれている)は、「有意差」依存を強く戒めているし、よりわかりやすく丁寧な説明が、佐藤俊哉(2024)『宇宙怪人しまりす 統計よりも重要なことを学ぶ』朝倉書店に書かれているので、一読をお勧めする。
ある程度仮説が確からしいことがわかった上で,因果関係を明らかにするために,集団を対象として行うのが介入研究である。典型的なのが,Randomized Controlled Trial (RCT:無作為化統制試験)である。例えば,新薬の有効性を調べたい時は,患者をランダムに2群に分け,片方は新薬を,もう一方は従来の標準的な薬を投与して,効果を比較する。この際,研究対象者も薬を投与する医師も,その薬が新薬なのか従来薬なのかがわからないようにして与えられる二重盲検(Double Blind)を行うのが普通である。
データを得る方法には,通常は問題発見型研究で行われるインタビューまたは質問紙(構造化/半構造化/非構造化(自由回答型)がある),観察(測定を含む),実験(動物実験やRCTを含む)に加えて,先行研究をまとめて再分析するシステマティックレビューないしメタアナリシスがある。
全数調査(悉皆調査)は,問題発見型研究に多い。母集団の基礎データを得るために実施されることがある。典型的な全数調査は国勢調査。国民健康・栄養調査のような標本調査をするための母集団の基礎情報は国勢調査から得られる。一般に用いられる統計学的手法は使えない。ただし,全数調査の中から標本を抽出して詳細な集計を行ったり関連性を調べたりすることは行われている(国勢調査の場合だと,約1%の調査票を使った速報集計や,抽出詳細集計がそれに当たる)。
統計解析の対象になるデータは,大抵の場合,標本調査によって得る。仮説検証型研究,動物実験,介入研究では適切な標本抽出(サンプリング)が必須である。臨床研究では,ある期間内に集まった症例数で妥協するしかない場合があるが,あくまで妥協と考えるべきである。原則として標本サイズはきちんと設計する必要がある(詳しくは後述)。動物実験や介入研究ではとくにクリティカル(サンプルサイズが小さくて検出力が足りなかったために有意な差が検出できなかったという言い訳は通用しない)。
最近流行のビッグデータは,(多くの場合自動的に記録される,従来のリレーショナルデータベースでは処理しきれないほど)大量のデータのことだが,全数調査ではない。かといって計画された標本調査でもない。本来,母集団が何かということに注意を払うべきだろうが,あまり考慮されていないようにみえる。しかし,手に入った範囲の大量のデータを短時間で高速に処理することで,限定的な特性の概略の傾向を掴むことがビッグデータ解析の目的であることが多いので,それでも実用上の意味はあるのだろう。
こうしてテーマに対するアプローチが決まったら,次にすることは,研究計画を立てることである。その後で研究を実施し,信頼できるデータを得て,データ解析をして,先行研究と比較しながら結果を解釈することになる。
大学院生の研究は,多くの場合,テーマを絞った問題解決型の標本調査になると思われるので,研究計画を立てる上で,サンプルサイズの計算が必須になる。そこで,先に進む前に,統計ソフトについて紹介しておく。現在では,SAS,JMP,SPSS等さまざまな統計解析ソフトが利用できるが,このテキストでは代表的なフリーソフトウェアであるRと,それをGUIで操作でき,医学統計解析向けの関数を整備したEZRを使った操作について説明する。神戸大学では図書館のコンピュータのSPSSのライセンス契約は2016年度末で切れたため,研究科としてもRまたはEZRを使うことが推奨されている。
RはMS Windows,Mac OS,Linuxなど,さまざまなOSで動作する。中間栄治さんが早い段階で開発に参加してくださったおかげで,テキスト画面でもグラフィック画面でも日本語の表示が可能だし,岡田昌史さんや間瀬茂さんを中心に組織されたユーザグループの協力によって,インターフェースの多くの部分で日本語に翻訳されたメッセージが利用可能である2。Windows版やMac OS版は,通常,実行形式になっているものをダウンロードしてインストールする。Linuxではtarで圧縮されたソースコードをダウンロードして,自分でコンパイルすることも難しくないが,ubuntuなどではコンパイル済みのバイナリを提供してくれている人もいるので,それを使う方が容易にインストールできるかもしれない。
Rはフリーソフトなので,自分のコンピュータにインストールすることも自由にできる。R関連のソフトウェアはCRAN (The Comprehensive R Archive Network)からダウンロードすることができる。CRANのミラーサイトが世界中に存在し,ダウンロードは国内のミラーサイトからすることが推奨されているので,日本では統計数理研究所のサイト3を利用すべきだろう。
2025年4月25日現在、Rの最新版は、4月11日にリリースされたR-4.5.0(コード名"How about a twenty-six?")である。Rはバージョンごとに開発コード名が付いているが、その出典が漫画Peanuts!なのは有名であり、R-4.5.0のコード名の出典は、ゼロでない何者かになりたいというチャーリー・ブラウンに対して、ルーシーが5? 26はどう? 1/72? わかった、平方根ね! と畳み掛ける途中で出てくる数字であり、たぶんとくに意味があるわけではない。2024年4月24日にリリースされたR-4.4.0の"Puppy Cup"は、スヌーピーが地域の子犬大賞にノミネートされて大騒ぎしたという話であった。ちなみに2月29日にリリースされていた4.3.3のコード名は"Angel Food Cake"で、道に迷ったチャーリー・ブラウンが、お腹が空いてAngel Food Cakeが食べたいなあ、と漏らすと、ウッドストックがレシピを語るというシュールな回、4.3.2の"Eye Holes"は、リリース日がハロウィン近かったので、子どもがハロウィンでお化けの仮装をするのに布に目出し穴を開けるのを忘れて見えない、というネタ、4.3.1のコード名は"Beagle Scouts"で、初出から50周年を記念する特設サイトができているくらい有名なテーマだった。
R-4.1.*からネイティブなパイプ記法が導入されるなど大きく機能追加された。2022年4月にリリースされたR-4.2.0でも大きな変化があり、とくにWindows版では、UTF-8をネイティブサポートしたため、R-4.1.*以前にShift-JISで書いていたコードをR-4.2.*のコンソールで開くと文字化けする(日本語コード指定できるエディタで変換するか、Chromeなどのブラウザで開いて文字化けしていない状態でコピーし、コンソールやスクリプトウィンドウにペーストすれば問題ない)。Rtoolsも4.2に変わった。MSVCRTではなくUCRTに依存しているためWindows10 (1903)以上でない場合、Rより先にUCRTのランタイムをインストールする必要がある。32ビット版もサポートしなくなるなど変化が大きいが、もはや大半のWindowsユーザはWindows 10かWindows 11で、64ビットプロセッサであろうから、個人的には良いと思う。グラフィックデバイスの扱いが変わり4、これまで入っていたパッケージもすべてRtools42以降を使ってビルドし直して再インストールする必要がある。2025年4月25日現在のRtoolsの最新版はRtools45である。
R-4.5.0-win.exe)をダウンロードし,ダブルクリックして実行する。インストール途中で,スタートアップオプションをカスタマイズするかどうか尋ねるダイアログが表示されるので,ここはいいえ(デフォルト)でなく,はい(カスタマイズする)の方をマークして「次へ」をクリックすることをお薦めする5。次に表示されるウィンドウでSDI (separate windows)にチェックを入れて「次へ」をクリックするのが重要である。他のオプションは好みに応じて選べば良い。なお,後でRcmdr/EZRをインストールしたい場合は,Windows自体のログインユーザ名に全角文字(2バイトコード)を使わない方が良い。R-4.5.0.tar.gzをダウンロードして展開して自力でコンパイルする。最新の環境であれば,./configureとmakeしてから,スーパーユーザになってmake installで済むことが多いが,場合によっては多少のパッチを当てる必要がある。なお、マルチコアのCPUに対応したRevolution Rが開発されていたが、開発していたRevolution Analytics社がMicrosoftに買収された後、引き続きMicrosoft R OpenとしてMRAN (Microsoft R Application Network) 7からダウンロードできる状態が暫く維持されていたものの、2023年7月1日にサイトが廃止された8。
以下の解説はWindows版による。基本的にLinux版でもMac OS X版でも大差ないが,使えるグラフィックデバイスやフォントなどが多少異なるので,適宜読み替えられたい。なお,以下の本文中,\記号は¥の半角と同じものを意味する。
Windowsでは,インストールが完了すると,デスクトップまたはクイック起動メニューにRのアイコンができている。Rguiを起動するには,デスクトップのRのアイコンをダブルクリックするだけでいい9。ウィンドウが開き,作業ディレクトリの.Rprofileが実行され,保存された作業環境.RDataが読まれて,
>と表示されて入力待ちになる。この記号>をプロンプトと呼ぶ。Rへの対話的なコマンド入力は,基本的にプロンプトに対して行う。閉じ括弧を付け忘れたり命令や関数の途中で改行してしまった場合はプロンプトが継続行を意味する+となることに注意されたい。なお,Windowsでは,どうしても継続行状態から抜けられなくなってしまった場合,キーを押すとプロンプトに戻ることができる。
入力した命令や関数は,「ファイル」メニューの「履歴の保存」で保存でき,後で「ファイル」のSourceで呼び出せば再現できる。プロンプトに対してsource("プログラムファイル名")としても同じことになる(但し,Windowsではファイルパス中,ディレクトリ(フォルダ)の区切りは/または\\で表すことに注意10。できるだけ1つの作業ディレクトリを決めて作業することにする方が簡単である)。
また,キーボードの↑を押せば既に入力したコマンドを呼び戻すことができる。
なお,Rをインストールしたディレクトリのbinにパスを通しておけば,Windows 8/8.1/10/11のコマンドプロンプトでRと打っても,Rを起動することができる。この場合は,コマンドプロンプトがRコンソールの代わりにシェルとして動作する。もっといえば,Makefileを書いておき,makeを使ってRを実行することもできる。下枠内のように書いたバッチファイル(make.cmdとか)を作っておき,INPUT.RにRのコードを書き,バッチファイルをダブルクリックして実行させ,結果がoutput.txtに保存されるように設定することもできる。
Rterm --vanilla < ./INPUT.R > output.txtq()<- 例えば,1,4,6という3つの数値からなるベクトルをXという変数に保存するには次のようにする。
X <- c(1, 4, 6)function() 例えば,平均と標準偏差を計算する関数meansd()の定義は次の通り。
meansd <- function(X) { list(mean(X), sd(X)) }install.packages() 例えば,CRANからRcmdrパッケージをダウンロードしてインストールするには,
install.packages("Rcmdr", dep=TRUE)dep=TRUEはdependency(依存)が真という意味で,Rcmdrが依存している,Rcmdr以外のパッケージ(かなりたくさんある)も自動的にダウンロードしてインストールしてくれる。なお,TRUEはTでも有効だが,誤ってTを変数として別の値を付値してしまっていると,意図しない動作をしてしまい,原因を見つけにくいバグの元になるので,できるだけTRUEとフルスペル書いておくことが推奨されている。? 例えば,t検定の関数t.testの解説をみるには,?t.testとする。関数定義は何行にも渡って行うことができ,最終行の値が戻り値となる。関数内の変数は局所化されているので,関数内で変数に付値しても,関数外には影響しない。関数内で変数の値を本当に変えてしまいたいときは,通常の付値でなくて,<<-(永続付値)を用いる。
このようなコマンドベースの使い方に習熟するには一定の時間が必要である。世界各地でRユーザが開発した追加機能パッケージが多数公開されているが,なかでもカナダ・マクマスタ大学のJohn Fox教授が開発したRcmdr(R Commander)は,メニュー形式でRを操作できるパッケージとして有名である。Rcmdrのメニューはカスタマイズすることができるし,プラグインという仕組みで機能追加もできるので,自治医科大学の神田善伸教授が医学統計向けにフルカスタマイズし機能追加したものがEZRである11。
R CommanderやEZRをインストールすれば,メニューから選んでいくだけで多くのRの機能を使うことができるので便利である。ただし,メニューに入っていない機能も多いので,必要に応じて,スクリプトウィンドウに直接Rの関数を打ち,実行したい範囲を選択して「実行」ボタンをクリックする必要がある。
EZRをインストールするには,Rcmdrをインストールした後で,
install.packages("RcmdrPlugin.EZR", dep=TRUE)と打てばよい12。
Rcmdrのメニューを起動するには,プロンプトに対してlibrary(Rcmdr)と打てばよい。暫く待てばR CommanderのGUIメニューが起動する。なお,いったんR Commanderを終了してしまうと,もう一度library(Rcmdr)と打ってもRcmdrは起動しないので,Commander()と打つ。ただし,detach(package:Rcmdr)と打ってRcmdrをアンロードしてからなら,もう一度library(Rcmdr)と打つことでR CommanderのGUIメニューを呼び出すことができる。
そこからEZRを呼び出すには,メニューの「ツール」から,「Rcmdrプラグインのロード」を選び,プラグインとしてRcmdrPlugin.EZRを選んでOKボタンをクリックする。少し待つと,「Rコマンダーを再起動しないとプラグインを利用できません。再起動しますか?」と尋ねるダイアログが表示されるので,「はい(Y)」をクリックするとEZRが起動する13。
なお,オリジナルのRcmdrメニューも「標準メニュー」として残っているので,EZRであってもRcmdrとしての標準的な使い方ができる。
Rには,Rcmdr/EZRの他にもいくつかのフロントエンドとなるソフトウェアが存在する。統計解析の機能としてはRを使うのだけれども,操作するためのフロントエンドとして,Rコンソールよりも多機能なソフトをかぶせることによって操作性を改善するものである。
統計解析の専門家やパッケージ開発者に人気なのが,RStudio14である。R本体と同様に,Windows版,MacOS版,Linux版が存在する。RStudioの利点はいろいろあるが,プロジェクトという単位でコードを管理できるのが大きい。パッケージ作成者がメンテをするには,ほぼ必須のツールといえる。オブジェクトの一覧が常時得られていて,それらの中身を確認する際もRコンソールより遙かに見やすい。ただ,Rcmdr/EZRとは組み合わせにくいので,たぶん初心者はRcmdr/EZRで,中級者以上になったらRStudioを使うのがいいだろう。筆者はRコードとそれをRtermを使って実行するためのスクリプトを書いてファイラからバッチ実行するという使い方をすることも多いが,普通はRStudioで十分である。
日本で開発されたフロントエンドで,フローチャートとして分析プロセスを操作するとコードが生成される点に特徴があるのが,R AnalyticFlow15である。分析の流れを可視化してくれるのは便利だし,他にも便利な機能は多い。これもR本体と同様,Windows版,MacOS版,Linux版が存在する。Rcmdr/EZRよりもコード実行を意識するし,RStudioよりもコードの流れはわかりやすいので,初心者が中級者に移行するときに役に立つかもしれない。デバッグ機能が優れているので,中級者以上でもRStudioよりR AnalyticFlowが好きだという人も珍しくない。
jamovi17も計算のバックエンドにはRを使うことができるが(Rのコードを出力させることができる),SPSSのようにデータの属性をビジュアルに指定し,表を見ながら統計手法を選んで使うソフトのようである。Rzに似ている思想と思われるが,パッケージではなくRStudio同様,独立したソフトウェアとしてインストールする。WindowsでもMacOSでもLinuxでも動作させることができる。
特筆すべきは,“Learning Statistics with jamovi”18というフリーテキストが提供されていることである。このテキストには,芝田征司氏による日本語訳『jamoviで学ぶ心理統計』19も存在する。元の“Learning Statistics with jamovi”は,David Foxcroft氏が,Danielle Navarro氏によるテキスト“Learning Statistics with R”20の使用ソフトをRからjamoviに置き換えて作成したものであり,心理統計の入門書としても大変参考になる。
最近では,SASやSPSSからもRを呼び出して使うことができるようになった。また,構造方程式モデリングのためにR本体への追加パッケージとしてsemやlavaanを用い,モデル自体をGUIで操作できるフロントエンドとしてΩnyx21を使うとか,階層ベイズモデルのためにRにはRStanパッケージをインストールして,Stan22と連動させて使うなど,高度な統計解析のために他のソフトウェアと連動させて使うことも広く行われている。このあたりが,Rのオープンさゆえの長所だと思う。
2016年に入り,2015年にRevolution社を買収したMicrosoftが,C#, Visual Basic, F#, C++, JavaScript, TypeScript, Pythonなど多くの言語の開発環境であるVisual StudioをRに対応させるR Tools for Visual Studio23をリリースした。他の言語でVisual Studioを使い慣れているプログラマにとっては便利かもしれない。
研究計画に入る前に,もう1つ説明しておかねばならない。統計解析を要する研究においては測定が必須であり,その測定は「正しく」なければならない。この章では,まず測定の正しさについて説明し,保健・医療の分野で集団を対象として正しい測定をするために必要な,疾病量と疾病量への効果を把握する疫学的な方法論の基礎について簡単に解説する。詳細はRothman (2012)などを参照されたい。
測定の正しさを考えるとき,少なくとも3種類の異なる正しさが存在することに注意したい。Validity (妥当性),Accurary(正しさ・正確性),Precision(精度)の3つである。
Validityとは,測りたいものを正しく測れていることである。例えば,ELISAで抗体の特異性が低いと,測定対象でないものまで測ってしまうことになるので,測定の妥当性が低くなる。途上国で子供の体重を調べる研究において,靴を履いた子供がいてもそのまま体重計に載せて,表示された値を使ったという研究があったが,そういうときの靴は往々にしてブーツなので1 kg近くの重さがある場合もあり,表示値そのままでは体重が正しく測れていない。また,測定すること自体が測定値に影響を与えてしまうと,妥当性は損なわれてしまう。例えば,心理的ストレスに対して何らかの物質の血中濃度が鋭敏に反応するとしても,採血自体がストレスを与えてしまう可能性があるので,その物質の測定値が高いという結果が出ても,元々ストレスが掛かっていたのか,採血がもたらしたストレスのせいで高値になったのか判別不能なので,短期的ストレス評価の指標として血液を含む侵襲的なサンプル採取を伴うと妥当性は損なわれる。もちろん,侵襲度が低ければ良いというものでもない。ストレス評価の場合,POMS-Jのような質問紙は非侵襲,心拍や唾液や光トポグラフィや脳波は低侵襲,血液は高侵襲だが,高侵襲な指標ほど真に測りたいものに近いので妥当性が高いことが多い。長期的なストレスを判定したい場合ならば,血液中の物質で,長期にわたる心理的ストレスに応じて高濃度になるが,短期的なストレスに対しての応答速度が速くない物質を測定すれば,妥当性が高くなる。ただし一般に,そこまで高い妥当性が必要でなければ低侵襲な方が倫理的に良い。
Accuracyとは,バイアス(系統誤差)が小さいことである。モノサシの原点が狂っていると(目盛幅が狂っているときも),正しさが損なわれる。例えば,何も載っていない状態で1 kgと表示されている体重計で体重を測定すると,真の体重が60 kgの人が載ったときの表示は61 kgとなるだろう。すべての人の体重が1 kg重く表示されたら,正しいデータは得られない。
Precisionは,確率的な誤差(ランダムな誤差)が小さいことである。信頼区間が狭い,CV(変動係数)が小さいこととも同義である。一般に感度の低い測定は精度が低くなる。例えば,手の大きさを測るのに,通常のものさし(最小表示目盛が1 mm)で測るのと,ノギス(最小表示目盛0.1 mm)で測るのでは,最小目盛の1/10まで読むとしても,精度が1桁異なる。
信頼性は安定性,再現性(test-retest reliability)や測定者間一致度(inter-observer concordance)や項目間一致度(Cronbachのα係数等)で示される。系統誤差がない場合,信頼性が高い測定ができれば,一般に妥当性もある。
本質的に直接測定が不可能な場合(質問紙によるストレス評価など),3種の妥当性を確保する必要があると言われてきた。
しかし,村山(2012)は,妥当性とは構成概念妥当性のことであり,他の「○△妥当性」は構成概念妥当性を検証するための方法・証拠のタイプと述べている。つまり,内容的証拠(専門家が妥当と判断するということ),収束的証拠(類似概念を知るためのテスト指標と高い相関があること),弁別的証拠(異なる概念を知るためのテストと低い相関しかないか無相関なこと),のように考えるべきとしている。
正確な測定には,ゼロ点調整が重要である。例えば,電子天秤で秤量するとき,試薬皿を載せた状態でtareしておかないと,試薬皿の重さだけ少なく量ってしまう。原点を通る検量線を描きたいとき,ブランクで吸光度がゼロになるように調整する(このときのブランクは水ではなく,対象物質の濃度がゼロで試薬は入っている,試薬ブランク)。
正確さを保証するには,例えば,標準物質の測定結果がcertified rangeに入っているかどうかを確認する(certified range自体の正しさは複数のreference laboでの測定で相互保証)。
正しい検量線を作る方法としては,以下2つが知られている。
精度を保つ方法としては,同一サンプルを繰り返し測定(またはduplicateやtriplicateで同時に測定)して,CVが小さいことを確かめることが,よく行われる。CV (Coefficient of Variation)とは,標準偏差を平均値で割った値(通常は100を掛けて%表記)である。
発想としては,測定値が真値±測定誤差の結果であり,測定誤差が平均ゼロの正規分布に従うと考え,誤差の標準偏差が測定値そのものに比べて十分小さい(例えば5%未満)なら測定値は信用できると考える。
異なるサンプルの測定値のばらつきを示すのにCVを使うのは誤用であり,その目的なら標準偏差そのものを見るべきである。また,サンプルから母集団におけるデータのばらつきを推定するには不偏標準偏差(不偏分散の平方根)を用いる。
サンプルから母集団の平均値を繰り返し推定した場合,その平均値がどの程度ばらつくか(即ち平均値の標準偏差)を示すのが標準誤差。サンプルから得られた不偏標準偏差をサンプルサイズの平方根で割った値になる。平均値が欲しいなら,標準誤差が小さいほど精度は高くなる。つまり,サンプルサイズが大きいほど精度は上がる。
疫学調査では,通常,「疾病/非疾病」と「曝露/非曝露」の関連性を調べるため,2つのカテゴリ変数間の関連性の程度をクロス集計により評価するのが普通である。
これを別の角度からみると,曝露群と非曝露群の間で,疾病量を比較することに相当する。疾病量の指標としては,prevalence(有病割合)またはodds(オッズ),risk(リスク),incidence rate(罹患率)を区別する必要がある。
疾病と曝露の関連性の程度【=effect(効果)】の評価法としては,difference(差)でみるか,ratio(比)でみるかを区別して考えるべきである。どちらも一長一短であり,目的に応じて使い分けるべきである(下表)。
| 疾病量の指標 | 差 (difference) | 比 (ratio) |
|---|---|---|
| 罹患率 (incidence rate) | 罹患率差(=率差) =曝露群の罹患率-非曝露群の罹患率 |
罹患率比(=率比) =曝露群の罹患率/非曝露群の罹患率 |
| リスク (risk) | リスク差 =曝露群のリスク-非曝露群のリスク | リスク比 =曝露群のリスク/非曝露群のリスク |
| オッズ (odds) | (なし) | オッズ比 =要因あり群の疾病オッズ/要因なし群の疾病オッズ =症例群の曝露オッズ/対照群の曝露オッズ |
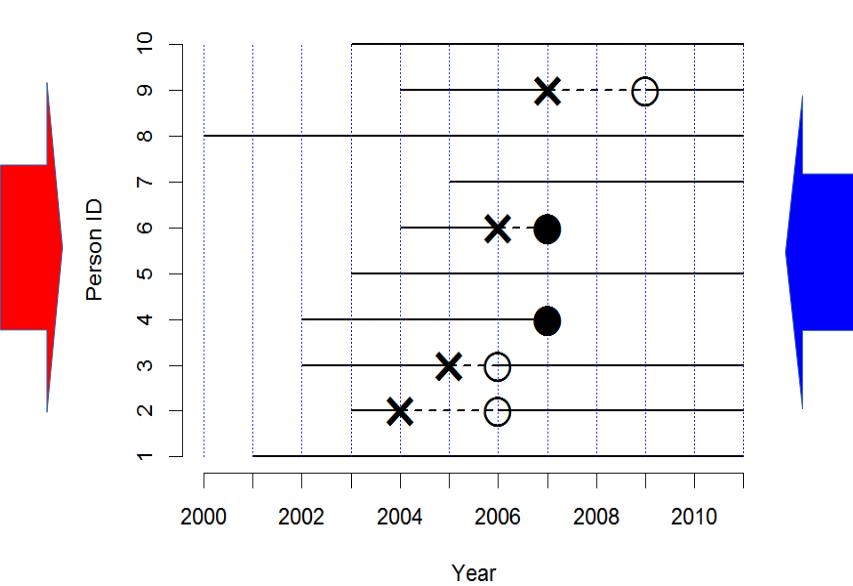
疾病発生の実際の状況を考えてみよう。下図では,横線のそれぞれが1人の個人を意味し,実線は健康,破線は疾病である状態を示す。×は疾病罹患,○は治癒,●は死亡を意味する。横軸は観察年を意味する。

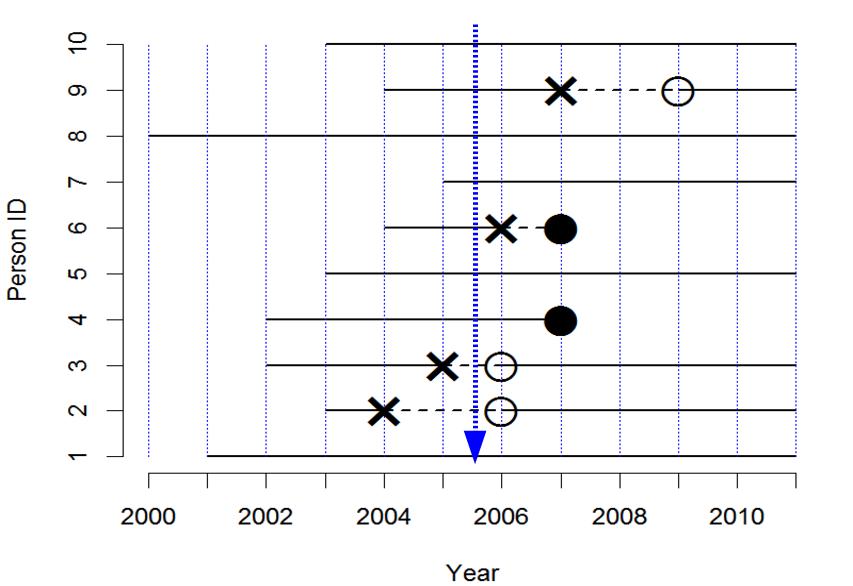
まず,有病割合 (prevalence)とは,ある時点で,全体の中でどれくらいの割合の人が病気かを意味し,以下のようにして求める。例えば,2005年半ばに横断研究をすると(下図青矢印),10人の人がいて,うち2人が病気なので,有病割合は2/10で0.2となる(なお,似て非なる概念である疾病オッズ24は2/8で0.25である)。調査が簡単なのが利点だが,2010年半ばに横断研究をすると,有病割合は0/8で0となってしまうこと(下図赤矢印)からわかるように,ある瞬間の情報しか与えてくれないという欠点がある。

次に,リスク (risk)は,累積罹患率 (cumulative incidence rate)ともいい,最初にいた観察対象人数を分母,観察期間内に病気を発症した人数を分子として求めた,罹患の確率を意味する。当然,観察期間が長いほど,大きい値になる傾向がある。2011年に生き残っている8人の子供について親に過去の罹患について思い出してもらい(下図青矢印),3人について疾病罹患が報告されたなら,この11年間のリスクは3/8=0.375と推定される。このような後ろ向きの研究は簡単で安価にできるが,既に亡くなった子供の情報を聞き逃してしまう欠点をもつ。逆に,2000年から11年間のコホート研究をした場合は(下図赤矢印),10人の子供のうち疾病罹患は4人が経験したので,11年間のリスクは0.4となる。ただし生後1年間に同じ病気に罹るリスクは1/10=0.1となる。この例から,リスクは観察期間に依存することが良くわかる。
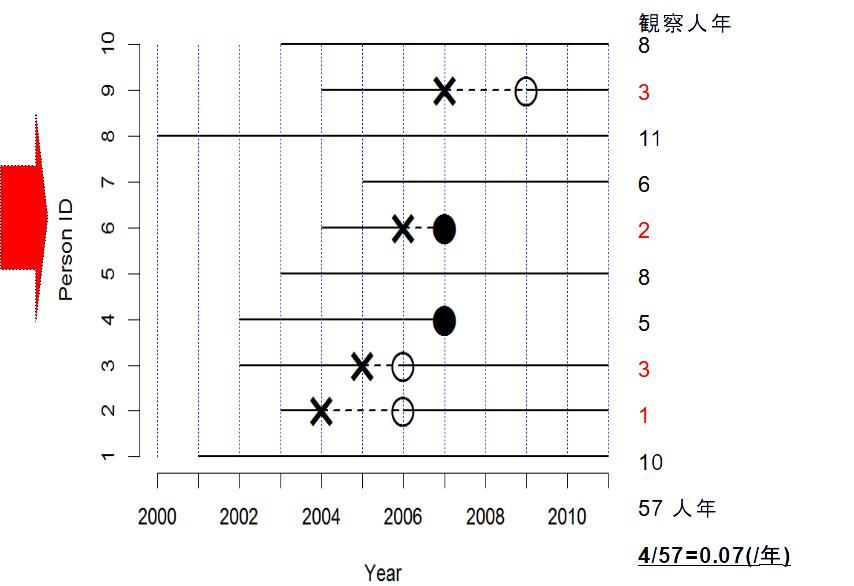
観察期間に依存しない指標を得るには,分母を人数でなく,延べ観察人年にすればよい。この発想で得られる指標が,罹患率 (incidence rate)である。上図赤矢印と同じく2000年からコホート研究すれば全人年データを観察できる25。下図のように数えた感受性のある観察期間の合計人年を分母,疾病発生数を分子にした値が「罹患率」(incidence rate)となる。罹患率は,(1/年)という次元をもつ(時間当たりの件数,即ち発生速度を意味する)。実際に計算してみると,57観察人年のうち4例発症しているから,4/57で約0.07(/年)となる。
なお,何度も罹患する疾病について,集団の罹患率を求めるには,年央のリスク人口を分母,その年の疾病発生数を分子とすると,罹患率が得られる(通常,10万人年当たりで計算する)。感染症サーベイランス事業で医師が診断したときに全数報告することになっている疾患については,報告数を年央人口で割ることによって毎年の罹患率が計算できるが,定点報告疾患や,あるいは罹患しても医療機関を受診しないような軽い疾患については,この方法で罹患率を求めることはできない。
観察のエンドポイントを疾病発生から死亡に変えると,罹患率の代わりに死亡率が計算できる。この例では,下図のように0.027/年となる。罹患率と同様に,大集団についての指標としては,年間死亡数を年央人口で割るとその年の死亡率が得られる(通常,1000人年または10万人年当たりで表す)。この例は小標本だから不適切だが,仮に下図で計算すると,2007年に0.2/年,他の年は0となる。

典型的な比較方法には,差(絶対比較)と比(相対比較)がある。両方ともそれぞれ意味がある。
比較する疾病量による違いがあり,リスクの場合は,リスク差またはリスク比を求める。罹患率の場合は,罹患率差または罹患率比を求める。また,死亡率の場合は死亡率差または死亡率比を求める(これらを総称して率差とか率比とかいう)。しかし,有病割合の場合は,オッズ比を用いるのが普通であり,有病割合の差を比べることはあまりない。
絶対比較は,リスク差または率差による。疫学では寄与危険とか超過危険と呼ぶ。
架空の例を考えてみる。高圧線の近くの住民10万人(曝露群)を5年間追跡調査して,毎年2人ずつ白血病患者が見つかったとする。高圧線から離れたところの住民10万人(非曝露群)を同じ期間追跡調査して,毎年1人ずつ白血病患者が見つかったとする。この人たちに居住地以外の(教育歴とか年収とか人種とか気候とか)違いはないものとする。
このとき,リスク差は, 10/100000 − 5/100000 = 5/100000( = 0.00005)
罹患率差は, 10/(100000 + 99998 + 99996 + 99994 + 99992) − 5/(100000 + 99999 + 99998 + 99997 + 99996) ≒ 0.0000100006(/year)
罹患率自体が非常に小さいので,差は小さく見える。
同じ例で,リスク比と罹患率比を考えてみる。 リスク比は, (10/100000)/(5/100000) = 2
罹患率比は,  ≒ 2
≒ 2
どちらの値も,「高圧線の近くに住むと白血病のリスクが約2倍になる」ことを意味する。統計学的に有意かどうかを調べるには,「母集団における比が1」という帰無仮説を検定する。R (EZR), SAS, JMPのようなソフトを使えば簡単で,p値は0.2より少し小さい程度なので有意水準5%では有意でない(fmsbパッケージを使って,下枠内のようにRコンソールで打てば,点推定量とともに,95%信頼区間やp値も示される)。
library(fmsb)
riskratio(10, 5, 100000, 100000)
rateratio(10, 5, 100000+99998+99996+99994+99992,
100000+99999+99998+99997+99996)先に示した例で,2005年に横断的研究をしたときのオッズ比を考えてみる。下図の状況である。
横断的研究では有病割合が疾病量の指標になる。しかし通常,有病割合そのものの差や比は評価しない。代わりにオッズ比を計算する。ここで,偶数番号の人が喫煙者,奇数番号が非喫煙者だったとする。喫煙者の疾病オッズは1/4,非喫煙者の疾病オッズも1/4となるので,オッズ比は(1/4)/(1/4) = 1となる。
症例対照研究では,オッズ比は症例の曝露オッズ(曝露有りの人数の曝露無しの人数に対する比)を対照の曝露オッズで割った値になる。もし2005年に2番と3番の人が症例として見つかった人で,他の8人が対照として標本抽出された人だったとすると(かつ偶数番号の人が喫煙者),オッズ比は (1/1) / (4/4) = 1となり,これら2つのオッズ比は一致する。
白血病の例では,有病割合が低いので,横断的研究で十分な検出力を得るためには大きなサンプルサイズが必要になるし,コホート研究で高圧線の近くに住むことの影響を調べるデザインも,比較的大きなサンプルサイズと長期間の観察を必要とするので効率が悪い。そのため,症例対照研究で,ある病院を一定期間に受診した白血病患者全員を症例とし,同じ病院を外傷で受診した人を対照としてリクルートし,居住場所が高圧線の近くかどうかを尋ねるのが常道である。
例えば,白血病患者100人のうち,高圧線の近くに住んでいる人が20人,外傷患者200人のうち,高圧線の近くに住んでいる人が20人だったとすると,オッズ比は以下のように計算できる。 (20/80)/(20/180) = 18/8 = 2.25
このオッズ比の統計学的有意性を検定するのに,Rでは以下のようにする。fisher.test()関数とfmsbパッケージのoddsratio()関数では若干のずれがあるが,いずれもp値は0.05より小さく,高圧線の近くに住むことが,有意水準5%で統計学的に有意に白血病罹患と関連しているといえる。
> fisher.test(matrix(c(20, 80, 20, 180), 2)) #オッズ比は最尤法での反復推定値
> library(fmsb)
> oddsratio(20, 80, 20, 180) #定義通りのオッズ比,正規近似によるp値,信頼区間EZRの場合は,メニューの「統計解析」→「名義変数の解析」→「分割表の直接入力と解析」と進んで,表示されたウィンドウの中に2×2の分割表があるので,それぞれに20, 80, 20, 180と入力してOKボタンをクリックすれば,fisher.test()と同じ結果が得られる。
大学院在籍期間中に研究に応じてくれた患者の数が限られていたため,要因Yが結果Z(通常,その病気であること)と関連がないという特定の帰無仮説Xを検定するために,10人の患者(とそれに対応する1~3倍程度の対照群)しか調査できなかったとする。検定の結果,有意水準5%で帰無仮説Xは棄却されなかったとする。
公表バイアス(publication bias)を避けるためには,こういう,「統計学的に有意でない」結果も,“Lack of association ...”のようなタイトルを付けて投稿すべきである。しかし,おそらく査読者は,この研究結果が「有意でなかった」のは,サンプルサイズが小さかった(言い換えると,検出力が足りなかった)からと判定する。これは研究デザインの致命的な欠点なので,論文はリジェクトされる。
大学院生としては学位が欲しいので,ここで統計学者に助けを求めることが多いのだが,この段階ではもはや手遅れ(せいぜい言い訳の仕方を教えるくらいしかできない)。良くある悲劇である。
では,どうすれば良かったのだろうか? この研究は,仮説検定という枠組みで行われた。サンプルサイズを大きくすれば統計的検出力が大きくなることは既知なので,研究開始前に,十分な統計的検出力を得るために必要なサンプルサイズを決定することが可能なはずである。
つまり,サンプルサイズの検討をせずに研究を開始したのが,そもそもの間違いだった。データを得てしまった後でできるのは,次のような言い訳を書くことだけである。
こういう研究であっても,結果は将来のメタアナリシスに貢献するし,査読を通ることは時々ある。しかし,本当は,事前の計算から必要なサンプルサイズはこれくらいと予想されるけれども,稀な疾患なので期間内に研究対象とできる患者数はこれくらいと予想されるため,これだけの患者が集まったら分析する,と事前にデザインしておき,研究ノートあるいは短報の形で投稿すべきであろう26。
最近の医学統計のテキストをみると,サンプルサイズが小さすぎる研究は,価値のある相関や差を示すのに十分な検出力をもっていないので非倫理的であるし,サンプルサイズが大きすぎる研究も,研究対象者に対して,既に劣っていることが明らかになっている治療(処置)を受けさせる可能性があるので,同様に非倫理的であると書かれている。
多くの学術雑誌が今では査読のチェックリストをもっていて,その中には,方法のセクションにサンプルサイズを決定する過程が含まれているかどうかについての項目が入っているし,サンプルサイズの決定が研究の前に行われていて,事後的になされたのではないことを確認するように書かれていることが多い。
有名な学術雑誌の一つである英国医学雑誌(British Medical Journal)に,Altmanらが2000年に示した統計学ガイドラインでは,“Authors should include information on … the number of subjects studied and why that number of subjects was used.”(著者は,……研究対象者の人数と,どうしてその対象者数が用いられたのかについての情報を論文中に含めるべきである)と書かれている。
しかし,テキストの中には,サンプルサイズを計算しなくてよい,という言説もある。以下のような理由付けが与えられている。
質的研究やケースレポート,あるいは予備的研究やパイロットスタディでは,統計学的な検定や推定をしない場合があって,そういう研究ではサンプルサイズの計算は不要である。
記述的な研究では,測定値についての事前情報が存在しないのが普通であるため,サンプルサイズの計算が不可能なことも多い(通常,サンプルサイズ計算には,測定値の標準偏差が必要)。
実験研究の場合,経験則として,各群12個体という目安はある(3個体とか6個体にする場合もある。動物実験では純系の動物が使われるため,遺伝的多様性による個体差は無視できることが多く,比較的ばらつきが小さいからである)。主な要因によるクロス集計表を考え,セル(条件の組合せ)ごとの個体数が十分大きくなるような総個体数を確保せねばならない。
研究には,大別すると2つのタイプがある。既に説明したように,仮説検証では,研究前にサンプルサイズを計算することは常に必要である。
しかし,隠れた仮説を見つけ出したり,95%信頼区間を推定する記述的研究では,事前のサンプルサイズの計算は必ずしも要求されない。しかし,その場合は,サンプリングの適切性を評価するためのパワーアナリシス(検出力分析)を事後に実施することは可能である。
記述的研究では,小標本からの有病割合の推定は精度が低いか,ミスリーディングになることがある。例えば,有病割合を求めたいとき。20人を調べて2人が病気だった場合,有病割合は10%となるけれども,この10%は信頼性が低い。病気の人が1人増減しただけで,有病割合が5%も変わってしまう。サンプルサイズの計算をすることにより,十分に狭い信頼区間を得るためには何人調べれば良いかがわかる。
計算に必要な値は先行研究から得る。
ある狭さの信頼区間をもった平均値を推定するためのサンプルサイズを決定するのに必要な情報は次の3つである。
このとき,必要なサンプルサイズ(n)は次の式で得られる(ただし,qnorm(1− α/2)は,正規分布の1 − α/2パーセント点を意味する。通常,95%信頼区間を求めるには,97.5%点が必要になることに注意)。
n = qnorm(1− α/2)2 × 4 × SD2 / d2
(例)ある患者群において,収縮期血圧の平均値を,95%信頼区間が10 mmHgまたは5 mmHgに収まるように推定したいとする。先行研究から,標準偏差としては11.4 mmHgを使うことが妥当と考えられたとする。
95%信頼区間が10 mmHg幅でよければ, n = 1.962 × 4 × 11.42/102 = 19.97... = 20
しかし95%信頼区間を5 mmHg幅に収めたければ, n = 1.962 × 4 × 11.42/52 = 79.88... = 80
つまり,精度を2倍にするには,サンプルサイズを4倍にする必要がある。
次に,割合を推定する場合を示す。必要な情報は先行研究と割合を推定する目的から決まる,次の3つである。
必要なサンプルサイズを推定するための近似式は, n = qnorm(1− α/2)2 × 4 × p × (1−p) / d2
(例)成人集団における喘息の有病割合を,95%信頼区間が10%幅に収まるように推定したいとする。母集団における喘息の有病割合が10%とすると,p = 0.1,d = 0.1,α = 0.05なので,
n = 1.962 × 4 × 0.1 × (1 − 0.1)/0.12 = 1.962 × 36 = 138
仮説検定においてサンプルサイズの計算に必要な情報は,次の5種類である。
検定方法ごとに(もっといえば,どれも近似式なので教科書あるいはソフトウェアによっても)推定式は異なっている。
例えば,両側t検定で平均値を比べるときは,推定される標準偏差をSD,意味のある差をdとして(zαは正規分布の100αパーセント点を意味する。片側ならzα/2のところがzαとなる), n = 2 × (zα/2 − z1-β)2 × SD2/d2 + zα/22/4
カイ二乗検定で2つの標本比率の差を比べるときは,2つの集団において期待される比率をp1,p2として, n = (zα/2 − z1 − β)2 × {p1(1 − p1) + p2(1 − p2)}/(p1 − p2)2
これらはまったく異なる式であることが一目瞭然である。式で手計算するよりも,サンプルサイズ計算に特化したソフト(nQuery,PASS,PSなど)あるいは,一般的な統計解析ソフト(SAS,SPSS,STATA,EZR,R等)を使う方が便利である。
リハビリ中の患者を2群に分けて,電気刺激をしたときに,しないときに比べて,肘の屈曲角が大きくなるかどうか,平均値の比較をしたい例を考える。
先行研究から,屈曲が4度大きくなれば臨床的に重要な意味があると考えられ,屈曲角の増加の標準偏差は5度と考えられたとする。
「肘の屈曲角の増加に差は無い」という帰無仮説に対して有意水準5%,検出力90%の片側t検定をするために必要なサンプルサイズは, n = 2 × ( − 1.64 − 1.28)2 × 52/42 + ( − 1.64)2/4 = 27.3174
この結果から,各群28人いれば十分と考えられる(四捨五入でなく,それを上回る最小の人数であるべきなので,切り上げにすることに注意)。
実際には,諸事情により研究に参加した患者は,各群28人にはわずかに足りなかった。それでも,26人の患者に電気刺激をし,25人の患者に電気刺激をせずに,屈曲角の増加を測定したところ,彼らの屈曲角の増加は,それぞれ,16 ± 4.5と6.5 ± 3.4であった。2群の平均的な差は9.5 (95%CIは7.23から11.73)で,片側t検定の結果は,t=8.43, df=49, p < 0.001となり,有意水準5%で統計学的に有意な差があったといえる。
Methodsセクションには以下のように書き,
We designed the study to have 90% power to detect a 4-degree difference between the groups in the increased range of elbow flexion. Alpha was set at 0.05.
Resultsセクションには
Patients receiving electrical stimulation (n=26) increased their range of elbow flexion by a mean of 16 degrees with a standard deviation of 4.5, whereas patients in the control group (n=25) increased their range of flexion by a mean of only 6.5 degrees with a standard deviation of 3.4. This 9.5-degree difference between means was statistically significant (95%CI = 7.23 to 11.73 degrees; one-sided Student’s t test, t=8.43; df=49; p < 0.001).
のように書く(出典は2つの例文とも,Lang and Secic, 2006, pp.47;一部改変)28。
この英文には,期待される屈曲角の増加の標準偏差が5度であることや,計算に使われた式は書かれていない。ともに暗黙のうちに想定されるのが普通である。通常,計算に使ったソフトウェアとオプション指定を書いておけば,使った計算式も決まるので,式そのものを論文に書く必要は無い。
PS: Power and Sample Size Calculatorは,ヴァンダービルト大学で開発,公開されている,サンプルサイズの計算に特化したフリーソフトである。
https://biostat.app.vumc.org/wiki/Main/PowerSampleSizeからダウンロードできる。内蔵されている統計解析方法は,Survival (logrank test), t-test, Regression1, Regression2, Dichotomous (chisq-test), Mantel-Haenszelである。
特徴として挙げられるのは,サンプルサイズの計算を示す例文がテキストとして自動生成されることである29。なお,このソフトで指定できるオプションには,実験群と対照群のサイズの比(m)も含まれている。mは1にすることもあるが,2とか3にすることも珍しくない。
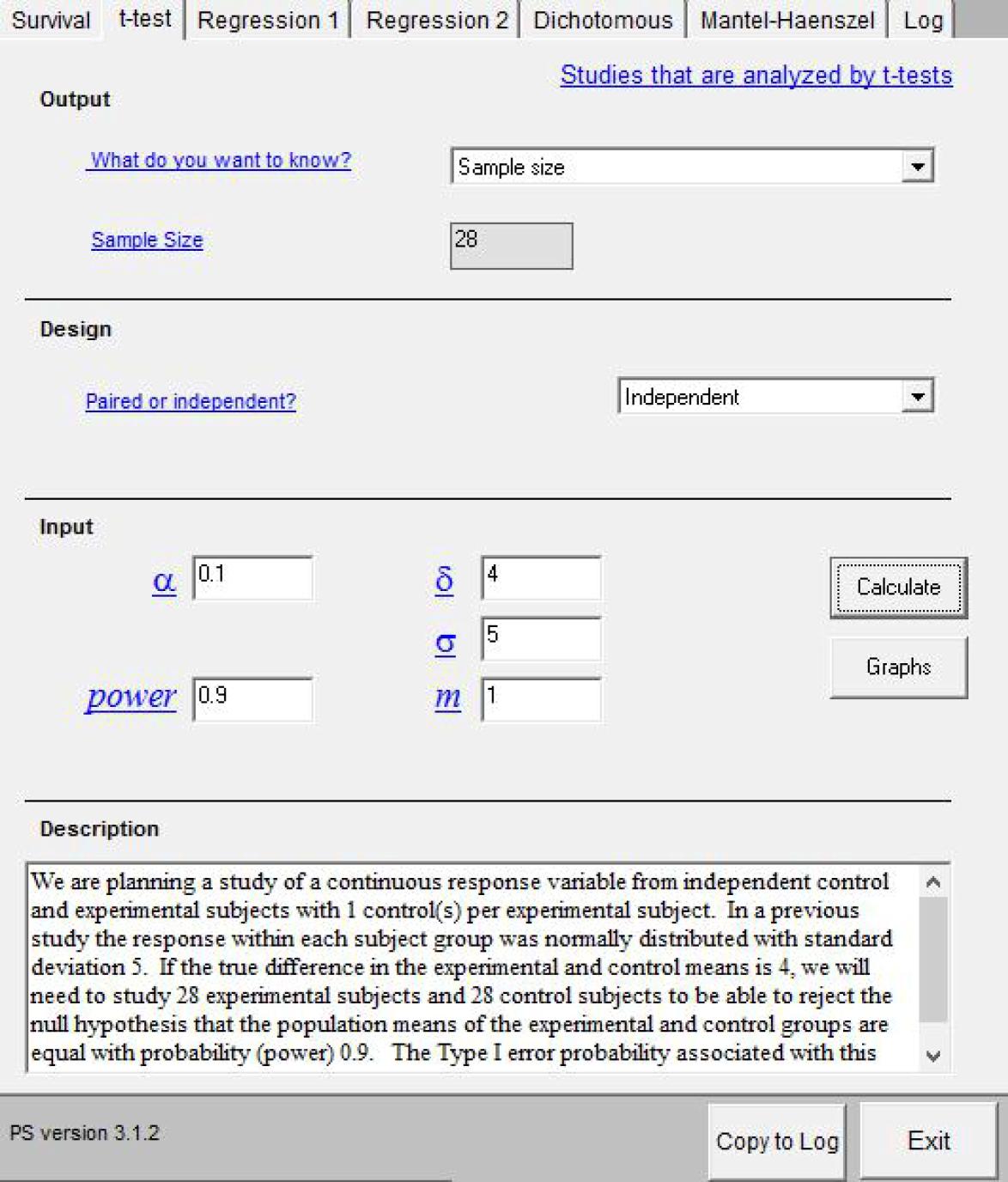
先に示した例でサンプルサイズを計算するには,PSを起動後,検定手法を選ぶタブの中からt-testを選び,求めるものはSample Size,サンプルの独立性はIndependentという順番で選び,δに4,σに5,αに0.1(片側5%なのだが,PSには片側検定の場合がないので両側10%で計算する),検出力に0.9,mに1と入力してから,「Calculate」ボタンをクリックすると,必要サンプルサイズが28と計算され,例文も自動生成される(下図)。
「統計解析」「必要サンプルサイズの計算」から条件を選ぶだけで完了する。この例では,メニューに表示される「2群の平均値の比較のためのサンプルサイズの計算」を選んで,下図のように,「2群間の平均値の差」のテキストボックスに4,「2群共通の標準偏差(SD)」のテキストボックスに5,「αエラー (0.0-1.0)」のテキストボックスに0.05,「検出力(1-βエラー)(0.0-1.0)」のテキストボックスに0.9,「グループ1と2のサンプルサイズの比(1:X)」のテキストボックスに1と入力し,解析方法のラジオボタンをOne-sidedにして「OK」ボタンをクリックすると,出力ウィンドウに各群27人という結果が得られる(One-sidedのところが両側ならば33人となる)。
> power.t.test(delta=4, sd=5, sig.level=0.05, power=0.9, alt="one.sided")
Two-sample t test power calculation
n = 27.46584
delta = 4
sd = 5
sig.level = 0.05
power = 0.9
alternative = one.sided
NOTE: n is number in *each* groupよって,必要なサンプルサイズは,各群28人となる。
サンプルサイズや検出力の計算専用のソフトとして、上述のPSは最近更新されていないので、G*Powerというソフトも便利である。ドイツのキール大学のFranz Faulによって開発されたソフトだが、多くの人が共同で維持管理しており、最新版は3.1.9.7である(マニュアルや本体がここからダウンロードできる)。ここで取り上げられている例をG*Powerで実行するには、起動後に、TestsというメニューのMeansからTwo Independent Groupsを選択し、Type of power analysisというメニューがA priori Compute required sample size - given α, power, and effect sizeとなっているのを確認し、Tail(s)というメニューでOneを選択する。
次にEffect size dを入力しなくてはいけないのだが不明なので、それを計算するために、その行の左側に表示されているDetermineというボタンをクリックする。すると、効果量を計算するためのダイアログが開く。この場合、平均値の差が4、標準偏差が2群とも5と考えられるので、Mean group 1に0、Mean group 2に4、SD σ group 1に5、SD σ group 2に5と打って、左下のCalculateというボタンをクリックする。Effect size dとして0.8と表示されるので、それを元のウィンドウのEffect size dの枠に手入力しても良いし、Calculate and transfer to main windowというボタンをクリックすると自動入力される。
α err probには想定している検定の有意水準0.05、Power (1-β err prob)には想定している検出力0.9、Allocation ratio N2/N1には2群のサンプルサイズの比1を入力し、右下のCalculateというボタンをクリックすると結果が得られる。下図に示すように、Sample size group 1、Sample size group 2とも28となっている。
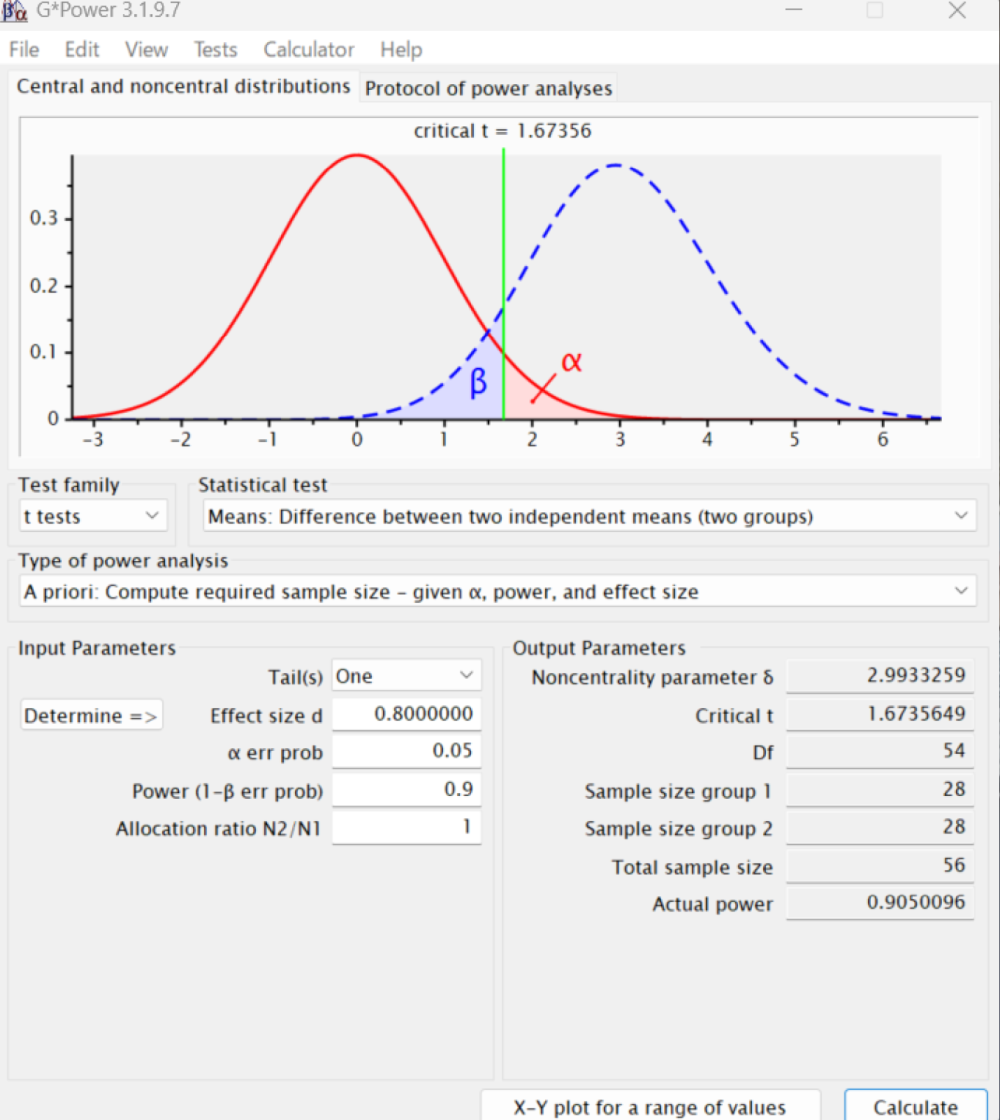
G*Powerでは、PSやEZRではサポートされていない、ロジスティック回帰分析のために必要なサンプルサイズの計算などもサポートされているので、使いこなせるようになると便利と思われる。
jamovi本体には入っていないが、jpowerモジュールやPAMLjモジュールを追加インストールすれば、jamoviでもサンプルサイズの計算は可能である。いずれも分析メニューのPowerというアイコンをクリックするとメニュー項目が表示される。独立2群間のt検定については、jpowerモジュールがIndependent Samples T-Testメニュー、PAMLjモジュールではT-testメニューを選ぶ。どちらの場合でも、G*Powerと同様に、意味がある(検出したい)平均値の差と期待される標準偏差ではなく、検出したい効果量を指定する。独立2群間のt検定での効果量は、平均値の差を標準偏差で割れば良い(2群に期待される標準偏差が異なる場合は、それらの2乗平均の平方根を求めて、2群共通の標準偏差として用いる)ので、この例では4/5で0.8を指定する。jpowerモジュールではMinimally-interesting effect size (δ)がデフォルトでは0.5となっているのを0.8に変えれば良い。Minimum desired powerはデフォルトが0.9なので、そのままで良い。α (type I error rate)もデフォルトが0.05なので、そのままで良い。Tailsをone-tailed (consistent)に変えれば、右側のウィンドウにN1とN2とも28と計算結果が表示される。PAMLjも指定方法は同様だが、得られる結果は2群を合計した56と表示される。PAMLjでは一般化線形モデルや構造方程式モデリングを当てはめるためのサンプルサイズの計算もサポートされている。
既に説明したとおり,研究には,大別すると,研究者が条件を設定しない研究(観察研究)と条件を設定する研究(実験研究や介入研究)がある。観察研究には,現状の記述を目的とする記述的研究と,仮説検証型の研究がある。
実験的研究では,動物実験でも臨床試験でも,研究者が条件設定できるので,注意深くデザインされねばならない。実験研究のデザインは,実験計画法として発展してきた。
実験計画法は,R.A. Fisherがロザムステッドで行った農学研究に始まるが,保健医療分野では,この種のデザインは,毒性試験や臨床試験で用量反応関係を分析するために必須である。もちろん,ヒトを対象にした研究は,実施前に倫理審査を通らねばならず,倫理審査に提出する書類には,適切なサンプルサイズの設定を含む,適切な研究デザインが記述されねばならない。
ケンブリッジのある晴れた日,多くの教授がアフタヌーンティーを楽しんでいた。と,ある婦人が,自分はミルクティーを飲めば,それがミルクが先か紅茶が先のどちらで淹れたものか判定できると主張した。世間一般の普通の人々は,そんなのどうでもいいじゃないかと思うかもしれないが,大学教授という人種は,そういうことに拘ることを生きがいにしている人が普通である。その場にいた教授たちの間で,当然のように,彼女の主張を廻って大激論が勃発した。先行研究があるわけでもなく,当然,収拾がつかない。
そこでR.A. Fisherが,「実験したらどうだい?」と言った。Fisherがいうには,この能力は,ミルクを先に入れて作ったミルクティーと紅茶を先に淹れて作ったミルクティーを何杯か用意して,無作為な順番で飲んで貰えば,確率論的に,どれくらい偶然ではありそうもないことかを判定できるというのだ。ここで大事なことは,能力の判定条件を考える必要があるということと,何回の繰り返しが必要かということだ。それを体系化した考え方が,上記3原則を含む実験計画法だというのである。
これは,「本当かどうかはわからないが」との注釈つきで,David Salsburgという人が,20世紀において,どのようにあらゆる科学に統計学が影響を与えてきたかについて書いた,“The lady tasting tea.”に掲載されているエピソードである。
ミルクティーの味の話がでてきたので,ここでちょっと余談。ロシア革命の混乱を風刺した小説『動物農場』や管理社会のディストピア小説として知られる『1984年』の作者であるジョージ・オーウェルは,無類の紅茶好きであり,「完璧な紅茶を淹れる11の法則」(Perfect Cuppa)30を次のように書いている(ストレートのダージリンに代表される,普通の「おいしい紅茶」の淹れ方とは随分違うが)。
George Orwell 「完璧な紅茶を淹れる11の法則」 (Perfect cuppa)
しかし,英国の王立化学会がGeorge Orwellの生誕100年を記念するパーティを開いたとき,Dr. Andrew Stapley (2003)は,次のように述べた。「冷えたミルクをカップの底に入れておいてから,熱い紅茶を注ぐのが良い。こうするとミルクが紅茶を冷ますことができる。逆だと熱い紅茶がミルクの温度を急に上げるのでミルクの風味が損なわれる」31。オーウェル推奨の順番は間違っているというわけである。
本当はどちらが先だとより美味しいのか,試してみた日本人ブロガーがいた。130ccの紅茶と30ccのタカナシ低温殺菌牛乳を使用した(高温殺菌とかロングライフのミルクでは違いが分からないらしい)。この方の主観的判断では,「ミルクが先」が美味だったとのことである32。
1杯ずつ増やして確率計算をしてみよう。
というわけで,本当は判別能力が無いのに偶然5回連続で正解する確率が,3.125% とわかる。この値は,偶然で片付けるには稀すぎる。通常,この判定基準は5%を切るかどうかにおく。これが有意水準(Fisher流)である。5回とも正しく判定されれば,帰無仮説「彼女は判定能力をもっていない」が有意水準5%で棄却される。
つまり,この仮説の統計学的検定には,少なくとも5杯のミルクティーを飲む必要がある。
実験計画法には,目的に応じて様々なデザインがある。有名なデザインをいくつか列挙しておく。
このデザインを使うと,研究者は,個々の対象者に対して同じ精度で測定された,何かの処理の前後で測定値に変化がないかどうかを評価することができる。通常使われる検定手法は,対応のあるt検定や,ウィルコクソンの符号順位検定になる。なお,対応のあるt検定は,個人ごとに算出した変化量の平均値がゼロという帰無仮説を検定する一標本t検定と,数学的には同値である。以下のような研究が典型的な例である。
EZRでの対応のあるt検定の実行例
EZRで,対応のあるt検定を実行する例を示す。対応のあるt検定自体は,事前-事後デザインに限らず,同一対象者に対して同じ精度で測定した値があれば適用可能なので,ここでは,Rには標準で含まれているMASSパッケージの,surveyデータフレームの,左右の手の大きさを比べる例を示す(このデータはアデレード大学で統計学を受講している学生237人に対する質問紙による横断的研究で得られた値であり,事前-事後デザインではない。出典:Venables and Ripley, 1999)。
このデータに含まれる変数のうち,Wr.Hndは,字を書く方の手を広げたときの大きさ,即ち親指の先端と小指の先端の距離であり,NW.Hndは,反対側の手を広げたときの大きさである。
EZRでの手順としては,まずデータをアクティブにする。「ツール」の「パッケージの読み込み」でMASSを選んでから,「ファイル」の「パッケージに含まれるデータを読み込む」から,パッケージとしてMASSをダブルクリックし,データフレームとしてsurveyをダブルクリックして「OK」ボタンをクリックすればよい。
次に,「統計解析」「連続変数の解析」から「対応のある2群間の平均値の比較(paired t検定)」を選ぶ。第1の変数としてWr.Hnd,第2の変数としてNW.Hndを選び(逆でも良い),「OK」ボタンをクリックすると,下枠内の結果が表示される。文字を書く手の方が,反対側の手よりも平均して0.086cm大きく,この差は統計学的に有意水準5%で有意であるとわかる。
Paired t-test
data: survey$Wr.Hnd and survey$NW.Hnd
t = 2.1268, df = 235, p-value = 0.03448
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
0.006367389 0.166513967
sample estimates:
mean of the differences
0.08644068既に述べたように,対応のあるt検定は差の平均がゼロという一標本t検定と数学的にまったく同じである。数式でも簡単に説明しておく,サンプルサイズnの標本のi番目の人について,対応のある2つの変数XとYの値をXi,Yiと書けば,XとYに差がないという帰無仮説は,Zi = Xi − Yiとして計算される「差の変数」Zの標本平均が母平均0と差がないという帰無仮説に帰着する。このとき,検定統計量t0は,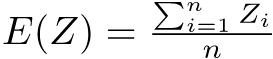 として,
として,  が自由度n − 1のt分布に従うことを使って検定できる。
が自由度n − 1のt分布に従うことを使って検定できる。
練習問題
珈琲を飲む前後で,計算問題の得点が変わるかどうか比べる。EZRでは,まずデータを作る。「ファイル」「新しいデータ」を選んでデータセット名を入力し(例えばcoffeeなどと名付ける),表計算のようなウィンドウでデータを入力する(1列目に珈琲を飲む前の得点を入力し,2列目に飲んだ後の得点を入力する)。各列の変数名の部分をクリックすると,変数名を入力したり,型が数値(numeric)か文字(character)かを指定することができる。
または,コンソールに
> scores <- data.frame(
+ precoffee=c(6, 5, 7, 6, 6, 7, 4, 5, 6, 7),
+ postcoffee=c(7, 8, 6, 7, 7, 8, 5, 6, 7, 7))と入力してもよい。
EZRの「統計解析」から「連続変数の解析」「対応のある2群間の平均値の比較(paired t検定)」と選んで,第1の変数としてprecoffee,第2の変数としてpostcoffeeを選べば,[t = -2.862, df = 9, p-value = 0.01872]と結果が出る。有意水準5%で統計学的に有意な差があるといえる。
これは非常に単純である。研究参加に同意した対象者各人に対して,完全にランダムに(行き当たりばったりに,ではなく),いくつかの処理(曝露)の1つを割り付け,処理間での比較をするというものである。
無作為化(randomization)の方法にはいくつかある。Fleiss JL (1986)“The design and analysis of clinical experiments”は,乱数表(random number table)の代わりに乱数順列表(random permutation table)を使うことを推奨している。
しかし,今ではコンピュータソフトが使えるので,紙の表を使わなくても,簡単にランダム割り付けはできる。Rの場合だと,例えば45人の対象者に対して3種類の処理を割り付けたいなら,次のようにする。
> matrix(sample(1:45, 45, replace=FALSE), 3)このままだと数字の出現順がバラバラで見にくいので,いったんxというオブジェクトに結果を付値して,それを行方向に小さい順に並べ替えて表示させるには以下のようにする。
> x <- matrix(sample(1:45, 45, replace=FALSE), 3)
> x[1,]
[1] 31 34 23 5 17 44 27 14 7 30 16 1 33 4 19
> apply(x, 1, sort)
[,1] [,2] [,3]
[1,] 1 2 8
[2,] 4 3 10
[3,] 5 6 11
[4,] 7 9 12
[5,] 14 13 20
[6,] 16 15 21
[7,] 17 18 22
[8,] 19 24 26
[9,] 23 25 28
[10,] 27 29 35
[11,] 30 32 39
[12,] 31 36 41
[13,] 33 37 42
[14,] 34 38 43
[15,] 44 40 45しかし,実際の研究では脱落が起こったりして,予定の人数に満たない場合がある。上の例でも,40人しか対象者が集まらないと,第2の処理を受ける人は15人いるが,第1の処理を受ける人は14人,第3の処理を受ける人はたった11人になってしまい,サンプルサイズがアンバランスになって検出力が落ちる。
このデザインによる研究の流れを下図に示す。このダイアグラムでは,研究対象者から得られる量的なデータを一元配置分散分析(oneway ANOVA)で分析し,割合のデータをカイ二乗検定で分析する。

何らかの事情で研究が完了しない場合,完全無作為化法では,既に述べたようにグループ間のサンプルサイズがアンバランスになる可能性がある。
この欠点を克服するのが乱塊法である。上述の例では,3種類の処理を15人ずつに適用する。3種類の処理を実施する順番は6通りなので33,1人ずつランダムに選ぶ代わりに,この6通りのブロックをランダムに15回選べば良いと考えられる。
そうすることによって,もし研究が途中で終わってしまっても,群間のサンプルサイズの差は最大1に抑えられる。記述と分析は完全無作為化法と基本的に同じだが,ブロックの効果を考慮した分析も可能である。
サイズバランスを保つ方法はもう一つあり,「最小化法」と呼ばれる。サンプリング時点ごとに群間のサンプルサイズの違いが最小になるような制約条件のもとでランダム割り付けを行う(あまりお薦めしない)。
2×2の要因配置法の例を示す。McMasterら (1985)は,乳がんの自己触診の教材としての小冊子とテープ/スライドを評価する無作為化試験を実施した。2種類の教材があるので,2×2の組合せで,4種類の平行群間試験としての実験をデザインできる。即ち,
このデザインでは,2種類の教材の教育効果は二元配置分散分析(Two-way ANOVA)を使って評価できる。
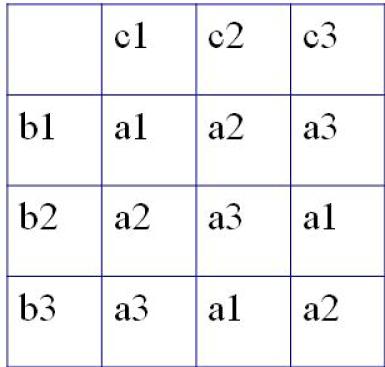
実験において,2つ以上の水準pがある処理Aの効果を評価したいとき,ともに同じ水準数pをもつ交絡因子BとCの影響を調整する必要がある場合に,このデザインが有効である。ラテン方格という名前は古代のパズルに起源がある。
ここではpが3であると仮定して説明する。ラテン方格は下図のようになる。最初のグループとしては,n1人の対象者について,a1b1c1という組合せの処理を行う。次のn2人は,グループ2として,a1b2c3という処理を受ける。残りも同じように図示した順番で処理を行う。そうすれば,アウトカム変数に対するBとCの効果を,分散分析(ANOVA)によって調整(除去)して,要因Aの効果を評価することができる(デザインの工夫によってBとCの効果は打ち消せると期待されるので,ターゲットであるAの効果だけを一元配置分散分析すれば良くなる)。
クロスオーバー法では,それぞれの対象者が2種類の処理を受ける。このとき,適当な間隔(ウォッシュアウト期間と呼ぶ。前の処理の影響のキャリーオーバーを避けるために設ける)をおくことと,処理の順番が違う2つのグループを設定することが必要である。
Hilman BC et al. “Intracutaneous immune serum globulin therapy in allergic children.”, JAMA. 1969; 207(5): 902-906.を例として説明しよう。
この研究では,同意が得られた574人から,まず研究目的に対して不適格な43人を除外し,531人をランダムに2群に分けた。グループ1が266人,グループ2が265人となった。グループ1に処理Aを行い,34人が脱落した。同時にグループ2には処理Bを行い,脱落が15人であった。その後,2ヶ月のウォッシュアウト期間をおき,グループ2の250人に処理Aを,グループ1の232人に処理Bを行ったところ,それぞれ45人,29人が脱落したので,2回の処理を完了したのは合計408人となった。
統計解析は,プレテストとして(1)キャリーオーバー効果が無視できるか検定(2群それぞれの2つの測定値の和の平均値の差の検定),それが確認できたら,(2)2群それぞれの差の平均値の差の検定,と実施すると良い(参考:Wellek S, Blettner M: Dtsch Arztebl Int. Apr 2012; 109(15): 276-281. doi: 10.3238/arztebl.2012.027634)
週刊医学界新聞の記事35が大変参考になるので読まれたい。
臨床試験を含む実験研究では,アウトカム(結果)の評価にいくつかのタイプがあり,それぞれ検定すべき帰無仮説が異なるため,サンプルサイズの設計法も異なる。
優性試験は,新しい処理群が対照群に比べて統計学的に有意に良い効果を示すかどうかを調べる。新薬の臨床試験などの場合に用いられる。「差がない」帰無仮説を検定して,p値が有意水準より小さければ帰無仮説を棄却する。
同等性試験は,新しい処理群が対照群と同じような効果を示すかどうかを調べる。検定でなく,「十分なサンプルサイズ」で正確に同等だというために信頼区間を用いる。事前に決めた「±○×%の差であれば臨床的に同等」とみなす同等性の許容範囲(同等性マージン,研究計画書にも記載)内なら同等とみなす。
非劣性試験は同等性試験の特殊な場合で,新しい処理が対照群に比べて劣っていないことを示せばいいとき,信頼区間を片側にすることでサンプルサイズを節約できるというアイディアに基づく。例えば,安価なジェネリック医薬品が従来薬に比べて薬効が劣っていなければいいという場合が典型的である。
実験計画法に基づく研究結果は,これまで書いてきたとおり,p値と帰無仮説の棄却,あるいは,差の信頼区間で示すのが普通である。しかし,1994年にCohenが“The earth is round (p < .05)”という論文を書いて有意水準批判をしたことから,アメリカ心理学会(APA)の推測統計に関する専門委員会が,統計解析の結果を報告する際のガイドラインを検討し,1999年に発表された提案において,信頼区間を使用した区間推定を示すことに加えて,重要な知見あるいはp値を報告するときは必ず効果量を報告することを含めたことから,心理学分野では統計改革が起こった。
APA Publication Manual 6th Edition (2009)では,具体的に,信頼区間をブラケットで示すことや,p値の後に効果量を記載することがAPAが発行する論文誌では最低限の要求であると書かれている。統計改革の流れは他分野にも波及したが,医学・保健学では信頼区間の重要性が強調され,生態学などフィールド生物学では統制が難しくサンプルサイズが小さいことが多いため検定力についての記載が求められることが多いので,効果量を記載することが必須になったのは,現状では,心理学分野と,質問紙調査で心理的尺度を用いる教育学や社会調査,疫学の一部にほぼ限られている36。
大久保・岡田(2012)による効果量(effect size)の定義は,「効果の大きさをあらわす統計的な指標のこと」で,「p値や検定統計量とは異なり,帰無仮説が正しくない程度を量的に表す指標」で,「帰無仮説が完全に正しい場合,一般に効果量は0,帰無仮説が正しくない場合は,正しくない程度が大きいほど効果量の絶対値も大きくなる」とのことである。仮説検定で帰無仮説が棄却できなくても効果量が0とは限らない点に注意が必要である。
一般に,検定統計量はサンプルサイズの関数と効果量の関数の積として表されることから,サンプルサイズが同じなら,効果量が大きいほど検定統計量は大きくなり,p値が小さくなることと,効果量が同じならば,サンプルサイズが大きいほど検定統計量が大きくなりp値が小さくなることが言える。サンプルサイズが大きくなると,ほとんど無視できるほど小さい効果量であっても,p値が0.05より小さくなることは普通にありうるので,数万人以上のサンプルサイズで有意水準を5%にした仮説検定などしても,実際的な意味はない。
効果量はサンプルサイズに依存しない(検定統計量からサンプルサイズに依存する部分を除去したものが効果量であるともいえる)のは,重要な性質である。以下,典型的な効果量をいくつか示す。
群間差についての効果量をd族の効果量と呼ぶ。三重大学奥村教授の解説37が参考になるが,2群間の平均値の差についてのCohenのdとHedgesのgが有名である。
Cohenのdは,標本の平均値の差を,標本のプールした標準偏差38で割って得られる,記述的な効果量である。言い換えると,2群の平均値の差が,プールした標準偏差の何倍かという値がCohenのdである。Hedgesのgは,Cohenのdを求める式において,標本のプールした標準偏差の代わりに,2群に共通な母分散を標本から推定する際の不偏推定量39を用いて得られる値である。spは不偏推定量ではないため,gも不偏推定量とはならないが,母標準偏差との差はspの方がSpよりも小さいことが知られているので,gの方がdより推奨されている。2群のサンプルサイズが等しい場合は,gに補正係数を掛けることによって得られる,バイアス補正したg(δ̂)を用いることもできる。補正係数J(n1 + n2 − 2)は次の式で得られる。 
Hedges(1981)はJ(n1 + n2 − 2)の近似式として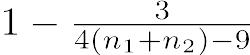 を提案している。
を提案している。
Rでは,effsizeパッケージのcohen.d()関数で,2群の値を示すベクトルをコンマで区切って与えるか,量の変数を第1引数,群の変数を第2引数としてコンマで区切って与えるかすれば,CohenのdまたはHedgesのgが得られ(後者が欲しいときはオプションとしてhedges.correction=TRUEを指定する),それらの効果量の信頼区間も得られ,効果量の大きさの目安として,絶対値が0.2未満だと無視できる(negligible),0.2以上0.5未満だと小さい(small),0.5以上0.8未満だと中程度(medium),0.8以上だと大きい(large)という判定を表示してくれて便利である。ただし,cohen.d()がCohen’s dとして表示するのは大久保・岡田(2012)でいうHedgesのgであり,Hedges’s gとして表示されるのがバイアス補正されたHedgesのgであることに注意されたい。
https://minato.sip21c.org/ebhc/dfamefs.R
dfamefs <- function(G1, G2) {
varp <- function(X) { sum((X-mean(X))^2)/length(X) }
J <- function(alpha) {
gamma(alpha/2)/(sqrt(alpha/2)*gamma((alpha-1)/2)) }
n1 <- length(G1)
n2 <- length(G2)
Sp <- sqrt((n1*varp(G1)+n2*varp(G2))/(n1+n2))
# Sp2 <- sqrt((n1*var(G1)+n2*var(G2))/(n1+n2))
# Sp3 <- sqrt(((n1-1)*(sd(G1)^2)+(n2-1)*(sd(G2)^2))/(n1+n2))
d <- (mean(G1)-mean(G2))/Sp
# d2 <- (mean(G1)-mean(G2))/Sp2
# d3 <- (mean(G1)-mean(G2))/Sp3
sp <- sqrt(((n1-1)*var(G1)+(n2-1)*var(G2))/(n1+n2-2))
g <- (mean(G1)-mean(G2))/sp
gadj <- g*(1-3/(4*(n1+n2)-9))
gadj2 <- g*J(n1+n2-2)
delta <- (mean(G1)-mean(G2))/sd(G2) # G2 has to be control
deltaadj <- (1-3/(4*length(G2)-5))*delta
return(list(Cohend=d, Hedgesg=g, gadj=gadj, gadjexaxt=gadj2,
Glassdelta=delta, deltaadj=deltaadj))
}
library(effsize)
G1 <- sleep$extra[sleep$group==1]
G2 <- sleep$extra[sleep$group==2]
cohen.d(G1, G2)
# cohen.d(sleep$extra, sleep$group)
cohen.d(G1, G2, hedges.correction=TRUE)
# cohen.d(sleep$extra, sleep$group, hedges.correction=TRUE)
dfamefs(G1, G2)
# Okubo, Okada (2012) Table 3.4
Exp <- c(59, 48, 51, 41, 39, 84, 95, 56, 86, 74)
Ctl <- c(47, 24, 38, 28, 39, 74, 77, 48, 40, 60)
cohen.d(Exp, Ctl)
cohen.d(Exp, Ctl, hedges.correction=TRUE)
dfamefs(Exp, Ctl)
}結果は以下の通り。
> cohen.d(G1, G2)
Cohen's d
d estimate: -0.8321811 (large)
95 percent confidence interval:
lower upper
-1.8115649 0.1472027
> cohen.d(G1, G2, hedges.correction=TRUE)
Hedges's g
g estimate: -0.7970185 (medium)
95 percent confidence interval:
lower upper
-1.7731697 0.1791327
> dfamefs(G1, G2)
$Cohend
[1] -0.8771959
$Hedgesg
[1] -0.8321811
$gadj
[1] -0.7970185
$gadjexaxt
[1] -0.7969352
$Glassdelta
[1] -0.7891127
$deltaadj
[1] -0.7214745> # Okubo, Okada (2012) Table 3.4
> Exp <- c(59, 48, 51, 41, 39, 84, 95, 56, 86, 74)
> Ctl <- c(47, 24, 38, 28, 39, 74, 77, 48, 40, 60)
>
> cohen.d(Exp, Ctl)
Cohen's d
d estimate: 0.8321811 (large)
95 percent confidence interval:
lower upper
-0.1472027 1.8115649
> cohen.d(Exp, Ctl, hedges.correction=TRUE)
Hedges's g
g estimate: 0.7970185 (medium)
95 percent confidence interval:
lower upper
-0.1791327 1.7731697
> dfamefs(Exp, Ctl)
$Cohend
[1] 0.8771959
$Hedgesg
[1] 0.8321811
$gadj
[1] 0.7970185
$gadjexaxt
[1] 0.7969352
$Glassdelta
[1] 0.8831702
$deltaadj
[1] 0.8074699変数間の関係の大きさを表す効果量をr族の効果量と呼ぶ。ピアソンの積率相関係数やポリシリアル相関係数,ポリコリック相関係数,回帰分析における決定係数,偏相関係数の二乗,分散分析におけるη2やηp2などは,すべてr族の効果量である。
研究によって得られたデータをコンピュータを使って統計的に分析するためには,まず,コンピュータにデータを入力する必要がある。データの規模や利用するソフトウェアによって,どういう入力方法が適当か(正しく入力でき,かつ効率が良いか)は異なってくる。
ごく小さな規模のデータについて単純な分析だけ行う場合,電卓で計算してもよいし,分析する手続きの中で直接数値を入れてしまってもよい。例えば,60 kg, 66 kg, 75 kgという3人の平均体重をRを使って求めるには,プロンプトに対してmean(c(60,66,75))または(60+66+75)/3と打てばいい。
しかし実際にはもっとサイズの大きなデータについて,いろいろな分析を行う場合が多いので,データ入力と分析は別々に行うのが普通である。そのためには,同じ調査を繰り返しするとか,きわめて大きなデータであるとかでなければ,Microsoft ExcelやLibreOffice Calcのような表計算ソフトで入力するのが手軽であろう。きわめて単純な例として,10人の対象者についての身長と体重のデータが次の表のように得られているとする。
| 対象者ID | 身長(cm) | 体重(kg) |
|---|---|---|
| 1 | 170 | 70 |
| 2 | 172 | 80 |
| 3 | 166 | 72 |
| 4 | 170 | 75 |
| 5 | 174 | 55 |
| 6 | 199 | 92 |
| 7 | 168 | 80 |
| 8 | 183 | 78 |
| 9 | 177 | 87 |
| 10 | 185 | 100 |
まずこれを表計算ソフトに入力する。一番上の行には変数名を入れる。日本語対応Rなら漢字やカタカナ,ひらがなも使えるが,半角英数字(半角ピリオドも使える)にしておくのが無難である。入力が終わったら,一旦,そのソフトの標準の形式で保存しておく(Excelならば*.xlsx形式,LibreOfficeのCalcならば*.ods形式)。
次に,この表をタブ区切りテキスト形式で保存する。Excelの場合は,メニューバーの「ファイル(F)」から「名前を付けて保存」を選び,現れるウィンドウの一番下の「ファイルの種類(T)」のプルダウンメニューから「テキスト(タブ区切り)(*.txt)」を選ぶと,自動的にその上の行のファイル名の拡張子もxlsxからtxtに変わるので,「保存 (S)」ボタンを押せばOKである(下のスクリーンショットを参照)40。複数のシートを含むブックの保存をサポートした形式でないとかいう警告が表示されるが無視して「はい」を選んでよい。その直後にExcelを終了しようとすると,何も変更していないのに「保存しますか」と聞く警告ウィンドウが現れるが,既に保存してあるので「いいえ」と答えてよい(「はい」を選んでも同じ内容が上書きされるだけであり問題はない)。この例では,desample.txtができる。
Rコンソールを使って,このデータをDatasetという名前のデータフレームに読み込むのは簡単で,次の1行を入力するだけでいい(ただしテキストファイルが保存されているディレクトリが作業ディレクトリになっていなくてはいけない)。
Dataset <- read.delim("desample.txt")
Rcmdrでのタブ区切りテキストデータの読み込みは,メニューバーの「データ」から「データのインポート」の「テキストファイルまたはクリップボードから」を開いて41,「データセット名を入力:」の欄に適当な参照名をつけ(変数名として使える文字列なら何でもよいのだが,デフォルトではDatasetとなっている),「フィールドの区切り記号」を「空白」から「タブ」に変えて(「タブ」の右にある○をクリックすればよい),OKボタンをクリックしてからデータファイルを選べばよい。
なお,データをファイル保存せず,Excel上で範囲を選択して「コピー」した直後であれば,「データのインポート」の「テキストファイル又はクリップボードから」を開いてデータセット名を付けた後,「クリップボードからデータを読み込む」の右のチェックボックスにチェックを入れておけば,(データファイルを選ばずに)OKボタンを押しただけでデータが読み込める。
Windows版では,R-2.9.0とRcmdr1.4-9以降なら,RODBCパッケージの機能によってExcelファイルを直接読み込むこともできる。「データ」の「データのインポート」の「from Excel, Access, or dBase dataset」を開いて42,「データセット名を入力:」の欄に適当な参照名をつけ,Excelファイルを開くとシートを選ぶウィンドウが出てくるので,データが入っているシートを選べば自動的に読み込める。
断面研究が典型的だが,1つの時点で多くの対象者から得たデータは,上述のように表形式にするのが容易である。複数のグループがあっても,グループを示すカテゴリ変数を作り,ともかく1人が1行に収まるようにすればよい。
コホート研究や繰り返し測定を含むデータの場合は,異なる時点で得たデータをどのように保持するかによって表の形が変わるため(あくまで1人を1行として入力する方が,後述する反復測定分散分析やフリードマンの検定をするには便利だし,1時点での測定値を1行とし,同じ人が複数行に出てくるように入力した方が作図や解析の目的次第では便利である),表形式にするよりもリレーショナルテータベースとしてデータベース構造を定義し,解析目的に応じてさまざまな表を出力できるようにした方が便利である。表計算ソフトを使う場合でも,時点ごとに別々のシートに入力すれば,ある程度この目的に対応できる。リレーショナルデータベースとしては,Microsoft OfficeならばAccess,LibreOfficeならばbaseとして含まれている。米国CDCが開発して無料で公開しているEpiInfoでは43,[Enter data]というメニューから,Access形式のデータベースを設計して入力・編集することができるようになっている。
経時的にとったデータの推移や,複数の時系列の相互作用を扱いたい場合は,データ構造が複雑になる。国によって暦法など時間情報を扱う単位が異なっていたり時差があったりするため,時間データベースが標準化されていて,時間情報解析ソフトというものも開発されている。HuTimeというソフト44は無料で利用できる。
地理情報もまた,表形式では扱いにくい情報である。バックグラウンドとなる地理情報と関連づけるためには,地理情報解析システム(GIS; Geographic Information System)を利用すると良い(詳細は非常勤でご出講いただく谷村先生の講義を参考にされたい)。高度な機能を使いたい場合はArcInfoというきわめて高価なソフトが標準的なソフトとして広まっているが,基本的な解析だけならば,QGIS45などのフリーソフトでも十分に実行できる。
なお,データ入力は,入力ミスを防ぐために,2人以上の人が同じデータを入力し,それを比較するプログラムを実行して誤りをチェックする方法がよいとされる。Excelのワークシートが2枚できたときに,それらを比較するには,1つのブックのSheet1とSheet2にそれらを貼り付けておき,Sheet3の一番左上のセル(A1)に,
=If(Sheet1!A1=Sheet2!A1,"","X")と入力し,これをコピーして,Sheet3上の全範囲(Sheet1とSheet2に参照されているデータがある範囲)に貼り付けると,誤りがあるセルにのみ"X"という文字が表示される。元データを参照してSheet1とSheet2の不一致部分をすべて正しく直し終われば,Sheet3が見かけ上空白になるはずである。
しかし,現実には2人の入力者を確保するのが困難なため,1人で2回入力して2人で入力する代わりにするか,あるいは1人で入力してプリントアウトした結果を元データと見比べてチェックするといった方法が使われることも多い。生データを自分で読み上げて録音し,再生音を聞きながら入力したデータをチェックする方法も,比較的効率は良い。
ここで注意しなければならないのは,欠損値の取扱いである。一般に,統計処理をする対象のデータは,母集団から標本抽出したサンプルについてのものである。サンプルデータを統計解析して,母集団についての情報を得るためには,そのサンプルが正しく母集団を代表していることが何より大切である。質問紙調査の場合でも,実験研究の場合でも,欠損値(質問紙なら無回答,非該当,わからない,等,実験研究なら検出限界以下,測定用の試料の量の不足,測定失敗等)をどのように扱うかによって,サンプルの代表性が歪められてしまうことがある。欠損が少なければあまり気にしなくていいが,たとえば,健診の際の食生活質問等で,「甘いものが好きですか」に対して無回答の人は,好きだけれどもそれが健康に悪いと判断されるだろうから答えたくない可能性があり,その人たちを分析から除くと,甘いもの好きの人の割合が,全体よりも少なめに偏った対象の分析になってしまう。なるべく欠損が少なくなるような努力をすべきだけれども,どうしても欠損のままに残ってしまった場合は,結果を解釈する際に注意する。
欠損値のコードは,通常,無回答(NA)と非該当と不十分な回答が区別できる形でコーディングするが,ソフトウェアの上で欠損値を欠損値として認識させるためのコードは,分析に使うソフトウェアによって異なっているので,それに合わせておくのも1つの方法である。デフォルトの欠損値記号は,RならNA,SASなら.(半角ピリオド)である。Excelではブランク(何も入力しない)にしておくと欠損値として扱われるが,入力段階で欠損値をブランクにしておくと,「入力し忘れたのか欠損値なのかが区別できない」という問題を生じるので,入力段階では決まった記号を入力しておいた方が良い。その上で,もし簡単な分析までExcelでするなら,すべての入力が完了してから,検索置換機能を使って(Excelなら「編集」の「置換」。「完全に同一なセルだけを検索する」にチェックを入れておく),欠損値記号をブランクに変換すれば用は足りる。
欠損コードの変更 実は欠損値を表すコードの方を変更することも可能である。例えばRではread.delim()などデータファイルを読み込む関数の中で,例えばna.string="-99"とオプション指定すれば,データファイル中の-99を欠損値として変換しながら読み込んでくれる。
次に問題になるのが,欠損値を含むデータをどう扱うかである。結果を解釈する上で一番紛れのない方法は,「1つでも無回答項目があったケースは分析対象から外す」ということである46(もちろん,非該当は欠損値ではあるが外してはならない)。その場合,統計ソフトに渡す前の段階で,そのケースのデータ全体(Excel上の1行)を削除してしまうのが簡単である(もちろん,元データは別名で保存しておいて,コピー上で行削除)。 質問紙調査の場合,たとえば100人を調査対象としてサンプリングして,調査できた人がそのうち80人で,無回答項目があった人が5人いたとすると,回収率(recovery rate)は80%(80/100)となり,有効回収率(effective recovery rate)が75%(75/100)となる。調査の信頼性を示す上で,これらの情報を明記することは重要である。目安としては有効回収率が80%程度は欲しい。
もう少し厳密に考えると,上述のごとくランダムでない欠損は補正のしようがないが,欠損がランダムな場合でも2通りの状況を分けて考える必要がある。即ち,MISSING COMPLETELY AT RANDOM (MCAR) の場合は単純に除去しても検出力が落ちるだけでバイアスはかからないが,MISSING AT RANDOM (MAR),つまり欠測となった人とそうでない人の間でその変数の分布には差が無いが他の変数の分布に差がある場合には,単純に除去してしまうとバイアスがかかるのである。そのため,multiple imputation(多重代入法)という欠損値を補う方法がいろいろ開発されている47。Rでは,mitools48とmice49という2つのパッケージがあり,後者のメインテナはDr. Stef van Buurenというオランダの方で,実はMultiple Imputation Onlineというサイト50のHeadをされている専門家である。ネット上の情報を眺めていると,たぶんmiceパッケージを使うのが良いと思われるが,まだ評価は定まっていないようである。最近ではAmeliaというパッケージがあり,高橋将宜・渡辺美智子『欠測データ処理:Rによる単一代入法と多重代入法』共立出版,ISBN978-4-320-11256-8で丁寧に使い方が紹介されている。
例えば,欠損のあるデータフレーム名をwithmissとすると,library(mice)の後で,imp <- mice(withmiss)とすると,元データやmultiple imputationによる欠損値推定の係数群がimpというオブジェクトに保存される。multiple imputationの方法は"sample","pmm","logreg","norm","lda","mean","polr"などから選べて,mice()関数のmeth=オプションで指定できる。欠損値が補完されたデータフレームを得るには,est <- complete(imp, 2)などとする。デフォルトでは5組の係数群が推定されるので,この例で指定した2により,そのうち2番目の係数群を使って推定されるデータフレームが得られる。あとは,このデータフレームを使って解析した複数の結果をまとめる必要がある。
無料で読める日本語による欠損値処理の説明としては,覚え書きとのことだが,村山航 (2011) 欠損データ分析(missing data analysis) ―完全情報最尤推定法と多重代入法―がわかりやすいと思う。英語だとcranのMissing DataのTask Viewやfinalfitというパッケージのvignetteがコンパクトでわかりやすい。
MARなのかMCARなのかを調べるLittleのMCAR検定については,mvnmleパッケージやBaylorEdPsychパッケージに含まれていたLittleMCAR()という関数があったが,どちらのパッケージも既にメンテナンスされなくなって久しく,cranから削除されている(Githubのcranアーカイヴに入っているので,devtoolsパッケージのinstall_github()関数を使ってcran/mvnmleのような指定をすればインストールできるが,メンテされていないパッケージを使うより,Little RJA (1988) A test of missing completely at random for multivariate data with missing values. Journal of the American Statistical Association, 83: 1198-1202.を読んで自分でコーディングした方が良い)。Task Viewに書かれている通り,RBtestパッケージでもMCAR性の検定ができるが,典拠となる文献が書かれていないし,回帰に基づく方法ということでLittleの方法とは違い,信頼できるかまだわからない。
データの大局的性質を把握するには,図示をするのが便利である。人間の視覚的認識能力は,パターン認識に関してはコンピュータより遥かに優れていると言われているから,それを生かさない手はない。また,入力ミスをチェックする上でも有効である。つまり,データ入力が終わったら,
何よりも先に図示をすべき
といえる。変数が表す尺度の種類によって,さまざまな図示の方法がある。離散変数の場合は,度数分布図,積み上げ棒グラフ,帯グラフ,円グラフが代表的であり,連続変数の場合はヒストグラム,正規確率プロット,箱ひげ図,散布図が代表的である。
以下,MASSパッケージに含まれているsurveyというデータフレームを使って作図する例を示す。
実際の作図に入る前に、色について簡単にまとめておく。修論などを見ていると、時々、カラー印刷される前提で、多数の色を使った図を見かけることがある。しかし、印刷物においてはモノクロになっても判別できるようにしておくことが重要である。投稿論文ではカラー図版には追加料金を請求されることが多いし、大学等のレギュレーションによって、正式に保存される論文はモノクロコピーであることが珍しくないからである。
したがって、印刷物(学会の抄録なども含めて)では、グラフの線は色分けではなく、実線、破線、一点鎖線のような線種で見分けがつくようにすることが望ましい。線だけでなく、データ点に打つシンボルの種類を変えることも有効な場合がある。領域も色による塗り分けではなく、角度や密度を変えたハッチングや粗さを変えた点描によって塗り分けるべきである。Rのコードでは、lty=というオプションで線種、lwd=で線の太さを指定できるようになっている関数が多い。図の中に凡例を明示することも必要である。
一方、学会発表や修論報告会などのプレゼンテーションにおいては、色分けが有効である。多くの関数で、col=というオプションにベクトル(整数または文字列。文字列は"black"のような色名でも有効だし、"#ffffff"のようにRGBに16進数2桁ずつを割り当てた文字列でも良い。"#ffffff77"のように最後の2桁で透過性を示すアルファチャンネルを指定することもできる)を与えることで色指定ができる。ただし、整数と色の対応関係のデフォルトの、1:黒、2:赤、3:緑、4:青、……という配色は、色覚多様性を考慮すると、必ずしも見分けやすくない。カラーユニバーサルデザインで推奨される配色セットを有効にするためには、palette("Okabe-Ito")を一度実行すれば良い。配色パレットが変わるので、それ以後ほとんどのグラフで使われる色が変わってくれる。グラフによっては領域塗りつぶしを重ねる必要がある場合があるが、その際はハッチングかアルファチャンネル指定を使うと良い。起動時に自動的にロードされるgrDevices関数に含まれているadjustcolor()関数を使えば、色名文字列と透過性を簡単に組み合わせることができる。
palette("Okabe-Ito") # カラーユニバーサルデザインの配色に
palette(adjustcolor(palette(), alpha.f=0.3)) # 配色そのままで透過度70%に
palette("R3") # R-3.*までのデフォルトパレットに
palette("default") # R-4.*のデフォルトパレットに
10人の身長・体重のデータでは作図の例示には向かないため,MASSパッケージに含まれているsurveyというデータフレームを使って説明する。MASSパッケージは推奨パッケージとしてWindows版のインストーラには元々含まれているし,RcmdrやEZRも依存しているので,別途インストールする必要はない。Rコンソールではlibrary(MASS)とするだけでがMASSパッケージがメモリにロードされ,surveyデータフレームが使える状態になる。
Rコマンダーでは,メニューの[ツール]の[パッケージのロード]を選んで表示されるウィンドウの中で,MASSを選ぶ。次に[データ]の[パッケージ内のデータ]の[アタッチされたパッケージからデータセットを読み込む]を選び,表示されるウィンドウの左の枠でMASSをダブルクリックし,次に右の枠でsurveyをダブルクリックし,[OK]ボタンをクリックする。
EZRでも,まずメニューの[ツール]の[パッケージのロード]を選んで表示されるウィンドウの中で,MASSを選ぶ51。「ファイル」メニューの「パッケージに含まれるデータを読み込む」から,パッケージとしてMASSをダブルクリックし,データセットとしてsurveyをダブルクリックしてから「OK」ボタンをクリックするだけでよい。
surveyというデータは,アデレード大学の学生237人の調査結果であり,含まれている変数は以下の通りである。
surveyの変数
barplot(table(X))で描画される。上記surveyデータでSmokeのカテゴリごとの度数分布図を描くには,
barplot(table(survey$Smoke))barplot(table(survey$Smoke)[c("Never", "Occas", "Regul", "Heavy")])survey$Smoke <- factor(survey$Smoke, levels=c("Never", "Occas", "Regul", "Heavy"))
barplot(table(survey$Smoke))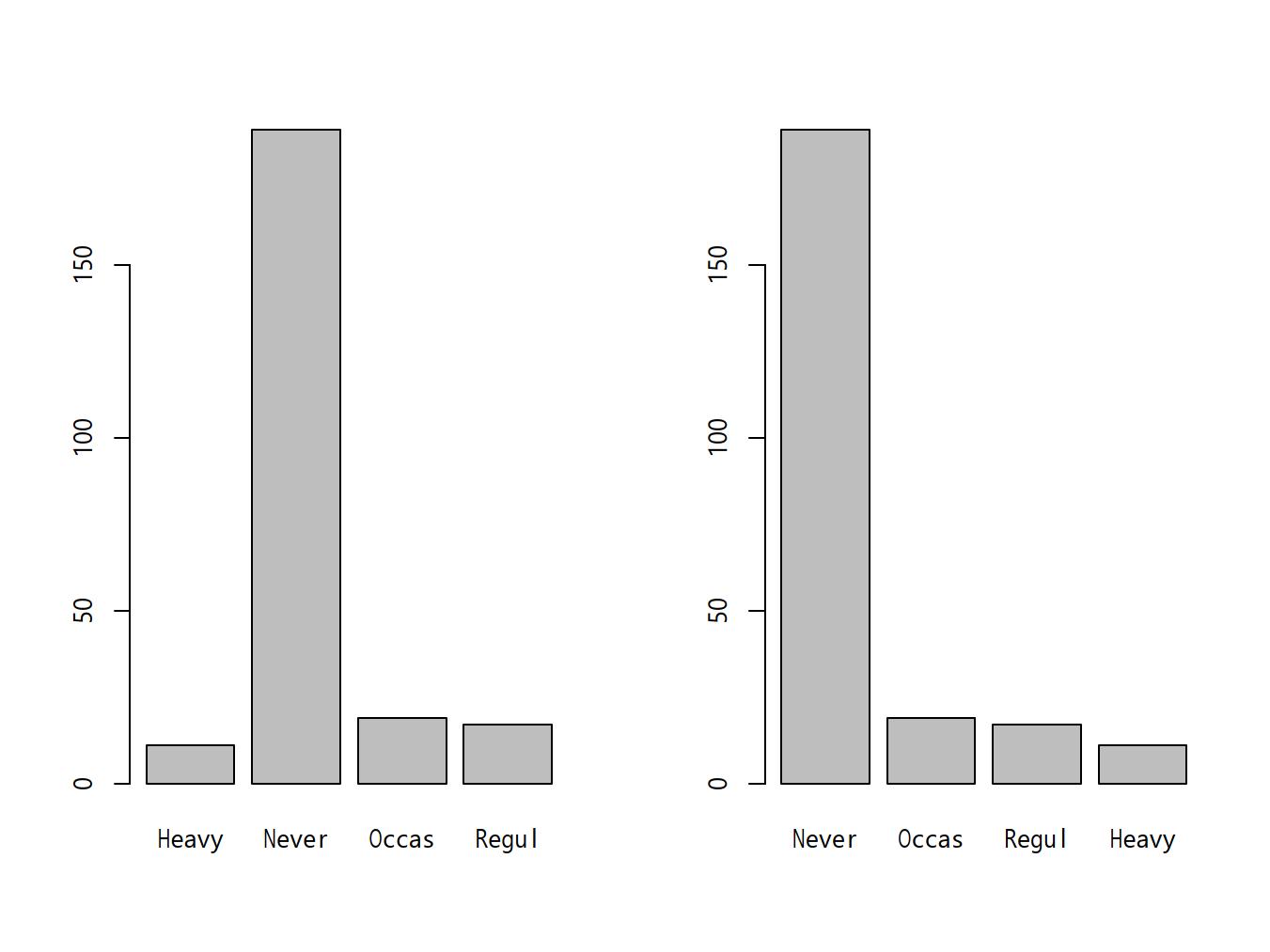 Rcmdrでは上記
Rcmdrでは上記surveyデータフレームをアクティブにした状態で,「グラフ」の「棒グラフ」を選び(EZRでは「グラフと表」「棒グラフ(頻度)」を選ぶ),「変数(1つ選択)」の中からSmokeを選んで「OK」をクリックすると,喫煙習慣ごとの人数がプロットされる。Smokeを選び,因子の名前は<元と同じ>となっているので変えず,「順序のある因子の作成」の右側のボックスにチェックを入れてから「OK」ボタンをクリックする。「変数Smokeが既に存在します。上書きしますか?」というダイアログが表示されるのでOKし(もし元のカテゴリ順序の情報がなくなるのが嫌なら,因子の名前のところに既存の変数名と重複しない新しい名前を入力しておけば,このダイアログは出ない。その場合は新しい変数が作られる),「新しい順序」に表示したい順番を入力して「OK」ボタンをクリックする。この操作をしてから,「グラフと表」「棒グラフ(頻度)」でグラフを作ればよい。surveyデータフレームの喫煙習慣について積み上げ棒グラフを描くには,Rコンソールでは
barplot(as.matrix(table(survey$Smoke)))barplot(table(survey$Smoke, survey$Sex))barplot(xtabs(~Smoke+Sex, data=survey))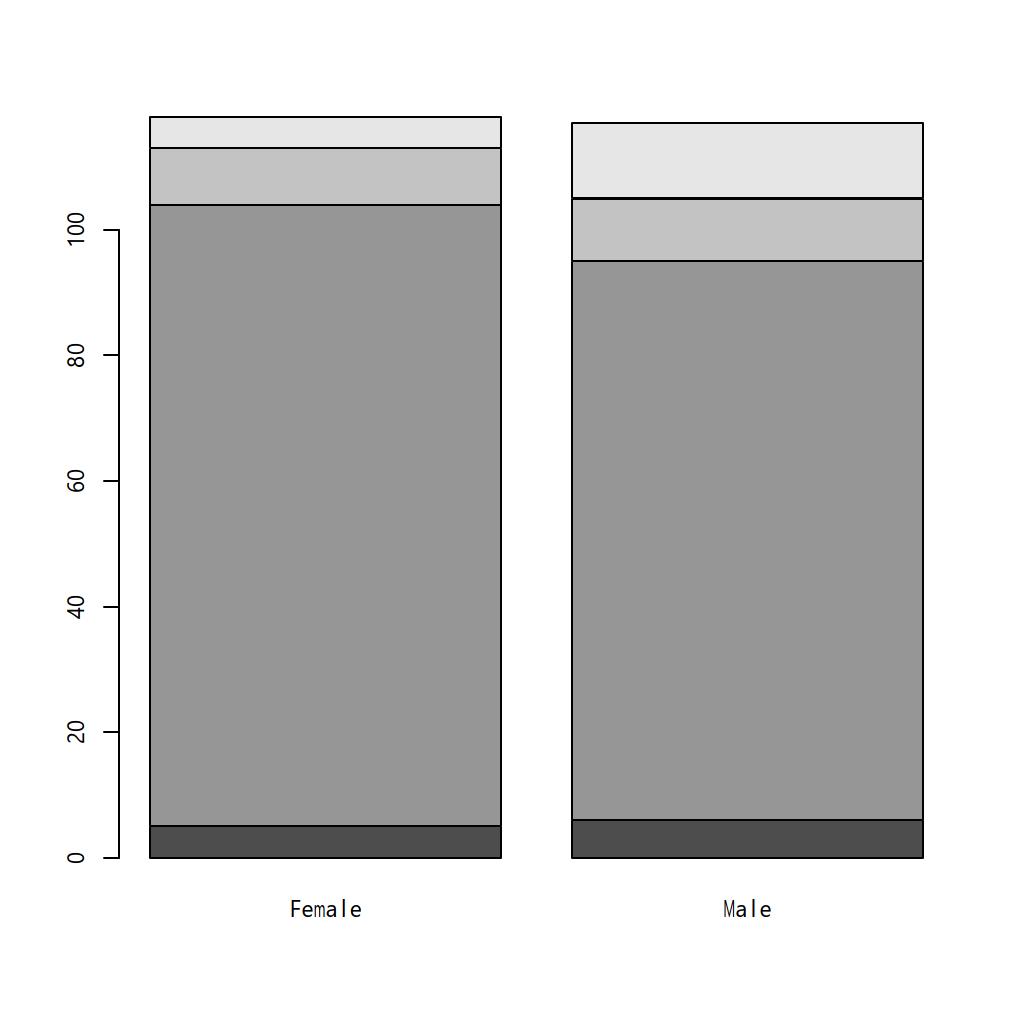
surveyデータフレームをアクティブにした状態で,「グラフと表」「棒グラフ(頻度)」を選び,「変数(1つ選択)」のところでSmokeを選ぶまでは度数分布を描くときと同じだが,「群別化変数1(0~1つ選択)」の中からもSexを選んで「OK」ボタンをクリックすることにより,層別積み上げ棒グラフを描くことができる。barplot(prop.table(table(survey$Smoke, survey$Sex), 2), horiz=TRUE)par(oma=c(0,0,0,6), xpd=NA)
Extent <- c("Never","Occas","Regul","Heavy")
FC <- rev(heat.colors(5)[1:4])
barplot(prop.table(table(survey$Smoke, survey$Sex)[Extent, ], 2),
horiz=TRUE, col=FC)
par(oma=c(0,0,0,0))
legend("right", fill=FC, legend=Extent)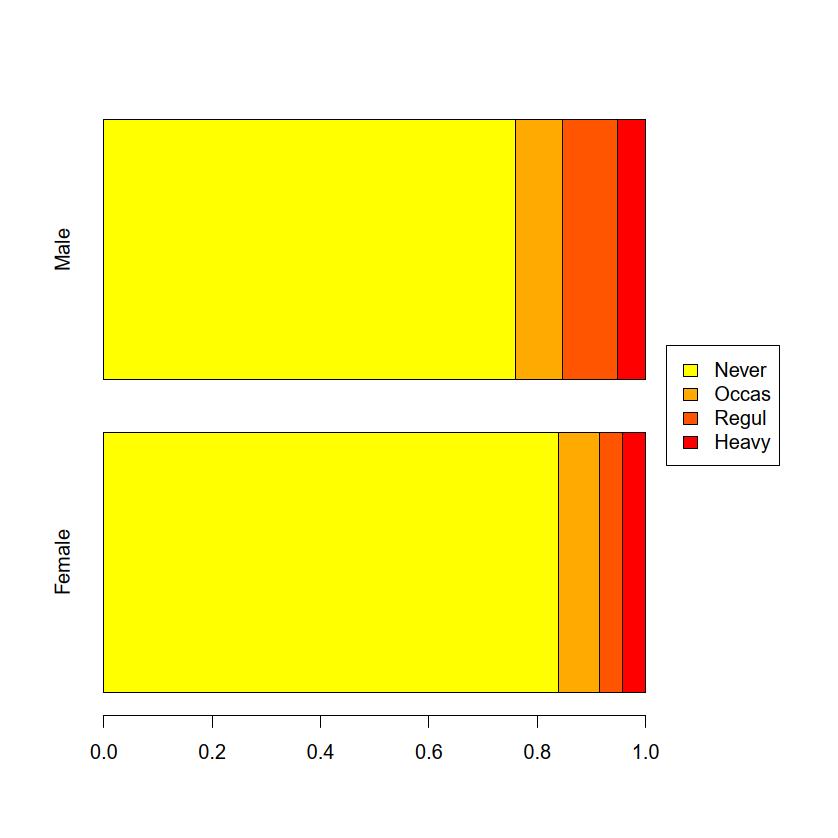
surveyデータフレームをアクティブにした状態で,「グラフと表」「棒グラフ(頻度)」を選び,「変数(1つ選択)」のところでSmokeを選び,「群別化変数1(0~1つ選択)」の中からもSexを選ぶところまで層別積み上げ棒グラフと同じで,さらに「群間の比較の場合に各群の中の割合で描画する」の左側のチェックボックスにチェックを入れてから「OK」ボタンをクリックすると,全体が100%になる。windowsFonts(JP1=windowsFont("MS Gothic"))
par(family="JP1")windowFont()の中はJP2, JP3などコンマで区切って複数のフォントを指定可能),選択してから「実行」ボタンをクリックし,出現するグラフィックウィンドウをそのままにして描画すれば,そこに描かれたグラフ要素はフォントがMSゴシックになるので,クリップボード経由でメタファイルとしてコピーペーストしても日本語が文字化けしなくなる。pie()関数を用いる。ただし錯覚しやすいのでお勧めしない。度数分布図の方が良い。surveyデータフレームをアクティブにした状態で,変数としてSmokeを選ぶと,喫煙習慣ごとの人数の割合に応じて円が分割された扇形に塗り分けられたグラフができる。hist()関数を用いる。デフォルトでは「適当な」区切り方として“Sturges”というアルゴリズムが使われるが,breaks=オプションにより明示的に区切りを与えることもできる。また,デフォルトでは区間が「~を超えて~以下」であり,日本で普通に用いられる「~以上~未満」ではないことにも注意されたい。「~以上~未満」にしたいときは,right=FALSEというオプションを付ければ良い。Rコンソールでsurveyデータフレームに含まれている年齢(Age)のヒストグラムを描かせるには,hist(survey$Age)だが,「10歳以上20歳未満」から10歳ごとの区切りでヒストグラムを描くように指定するには,
hist(survey$Age, breaks=1:8*10, right=FALSE, xlab="Age",
main="Histogram of Age")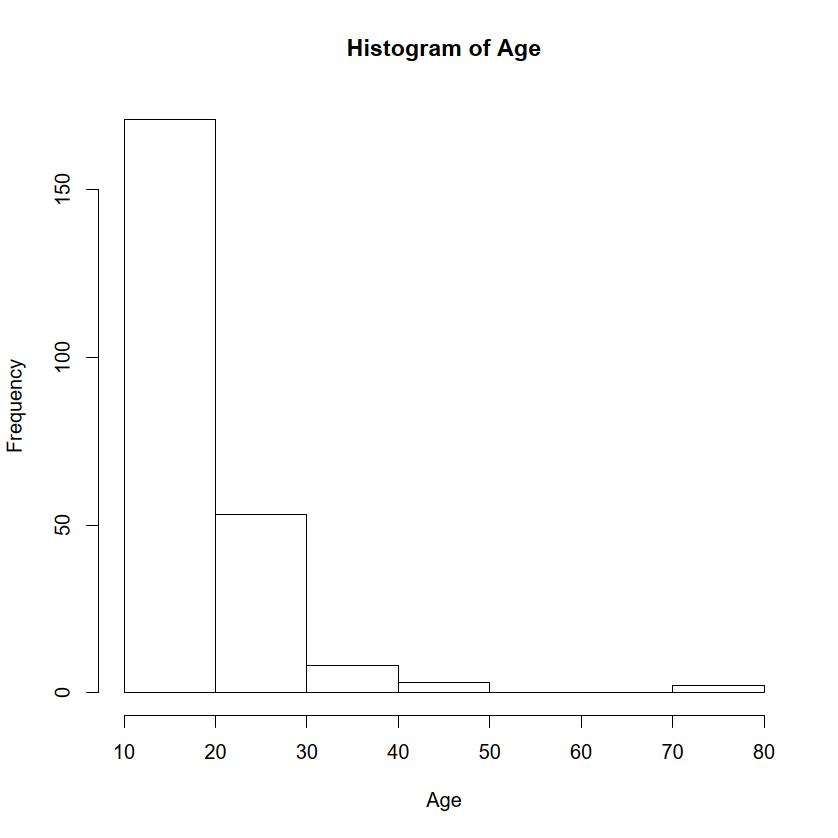
surveyデータでは,変数としてAgeを選べば,年齢のヒストグラムが描ける(アデレード大学の学生のデータのはずだが,70歳以上の人や16.75歳など,大学生らしくない年齢の人も含まれている)。RcmdrやEZRでは「~以上~未満」にはできない(裏技的には,予め「~以上~未満」のカテゴリデータに変換しておき,「棒グラフ(頻度)」で描画することはできるが,バーの間に隙間があるのはヒストグラムとしては正当でないのでお勧めしない)。qqnorm()関数を用いる(getS3method("qqnorm","default")とすると実際のコードの中身がわかる。中で使われているppoints()関数の定義を見るには,ppointsと打てばよい)。Pulse)について正規確率プロットを描くには,qqnorm(survey$Pulse)とする。以下のように打つと同じグラフになることを確認されたい。
rPulse <- sort(survey$Pulse)
n <- length(rPulse)
tNorm <- qnorm((1:n-ifelse(n<=10, 3/8, 1/2))/n)
plot(tNorm, rPulse, main="Normal QQ plot")surveyデータフレームでは,変数としてAgeを選ぶと,まったく正規分布でないので直線状でないし,Pulseを選ぶと,やや歪んでいるけれども概ね直線に乗るので正規分布に近いことがわかる。また,EZRでは,「統計解析」「連続変数の解析」「正規性の検定(Kolmogorov-Smirnov検定)」でも,正規性の検定が実施されるのと同時にヒストグラムに正規分布の曲線を重ね描きしてくれるので,正規分布と見なせるかどうかは見当がつく。stem()関数を用いる。同じデータで心拍数の幹葉表示をするには,stem(survey$Pulse)とする。
The decimal point is 1 digit(s) to the right of the |
3 | 5
4 | 0
4 | 88
5 | 004
5 | 569
6 | 000000000000122223444444444
6 | 555555666666788888888888888889
7 | 00000000000001122222222222222344444
7 | 5555566666666666668888999
8 | 0000000000000000001333344444
8 | 55556667788889
9 | 00000000222222
9 | 66678
10 | 0044fmsbパッケージのgstem()関数を使えばグラフィック画面に出力することもできる。Rcmdrには含まれていない。EZRでは「グラフと表」「幹葉表示」を選び,「変数(1つ選択)」の枠内からPulseを選んで「OK」ボタンをクリックすればOutputウィンドウにテキスト出力される。さまざまなオプションが指定可能である。boxplot()関数を用いる。例えば,surveyデータで喫煙状況(Smoke)別に心拍数(Pulse)の箱ヒゲ図を描くには次の2行のどちらかを打つ。
boxplot(survey$Pulse ~ survey$Smoke)
boxplot(Pulse ~ Smoke, data=survey)
Pulseを選び,[層別のプロット]というボタンをクリックして表示されるウィンドウで,層別変数としてSmokeを選んで[OK]ボタンをクリックしてから,戻ったウィンドウで再び[OK]をクリックすればいい(EZRの場合は「群別する変数(0~1つ選択)でSmokeを選び,上下のひげの位置として「第1四分位数-1.5x四分位範囲、第3四分位数+1.5x四分位範囲」の左のラジオボタンをチェックして「OK」をクリックするだけでよい)。Smoke,「目的変数」としてPulseを選べばよい。エラーバーとしては標準誤差(デフォルト),標準偏差,信頼区間から選択できる。plotrixパッケージかfmsbパッケージをインストールする必要がある。どちらもCRANのミラーサイトからダウンロードしてインストールできる。インターネットにつながったいる環境ならば,前者はinstall.packages("plotrix"),後者はinstall.packages("fmsb")とすればインストールできる。その上で,例えば後者の場合なら,library(fmsb)としてからexample(radarchart)とすれば使い方がわかる52。
RcmdrやEZRのメニューには入っていない。plot()関数を用いる(ただし,実はRのplot()関数は総称的関数なので,縦軸が数値変数で,横軸がカテゴリ変数であるときは自動的に層別箱ひげ図になる)。データ点に文字列を付記したい場合はtext()関数が使えるし,マウスで選んだデータ点にだけ文字列を付記したい場合はidentify()関数が使える。MASSパッケージのsurveyデータフレームに含まれるHeightを横軸に,Wr.Hndを縦軸にして散布図を描きたい場合は以下2行のどちらかを打つ。
plot(Wr.Hnd ~ Height, data=survey)
plot(survey$Height, survey$Wr.Hnd)plot(Wr.Hnd ~ Height, data=survey, pch=as.integer(Sex),
col=as.integer(Sex))legend("bottomright", pch=1:2, col=1:2, legend=c("Female", "Male"))とすればよい。points()関数を使って重ね打ちすることもできる。点ごとに異なる情報を示したい場合(異なる大きさの円でプロットするなど)はsymbols()関数を用いることができる。
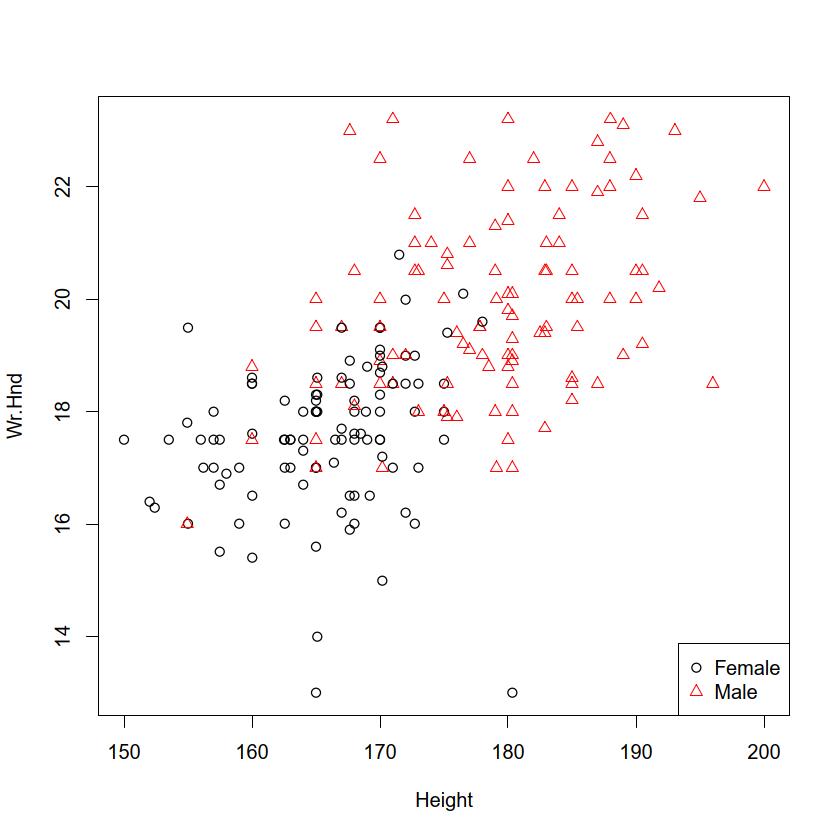
Rcmdrでは「グラフ」「散布図」,EZRでは「グラフと表」「散布図」を選び,「x変数(1つ選択)」からHeightを,「y変数(1つ選択)」からWr.Hndを選んで,「周辺箱ひげ図」と「最小2乗直線」(Rcmdrでは「平滑線」)の左のボックスのチェックを外してから「OK」をクリックすれば,上と同じような図が描ける。オプション指定で層別にマークを変えることもできる。[層別のプロット]ボタンをクリックして層別変数としてSexを選べばよい。できあがった散布図の点をマウスでクリックして値を確認したい時は,x変数やy変数を指定するウィンドウで,「点を確認する」にチェックを入れておく。確認したい点の上で左クリックするとレコード番号が表示され,右クリックするまで繰り返すことができる。
複数の連続変数間の関係を調べたい場合は,matplot()関数とmatpoints()関数を使って重ね描きすることもできるが,別々のグラフとして並べて同時に示す「散布図行列」を描画するのが便利である。pairs()関数を用いる。例えば,MASSパッケージのsurveyデータフレームに含まれるすべての数値型変数(Wr.Hnd,NW.Hnd,Pulse,Height,Age)について散布図行列を作りたいときは,
pairs(subset(survey, select=sapply(survey, is.numeric)))Wr.Hnd,Pulse,Ageの3つの関係だけを調べたいなら,
pairs(~ Wr.Hnd+Pulse+Age, data=survey)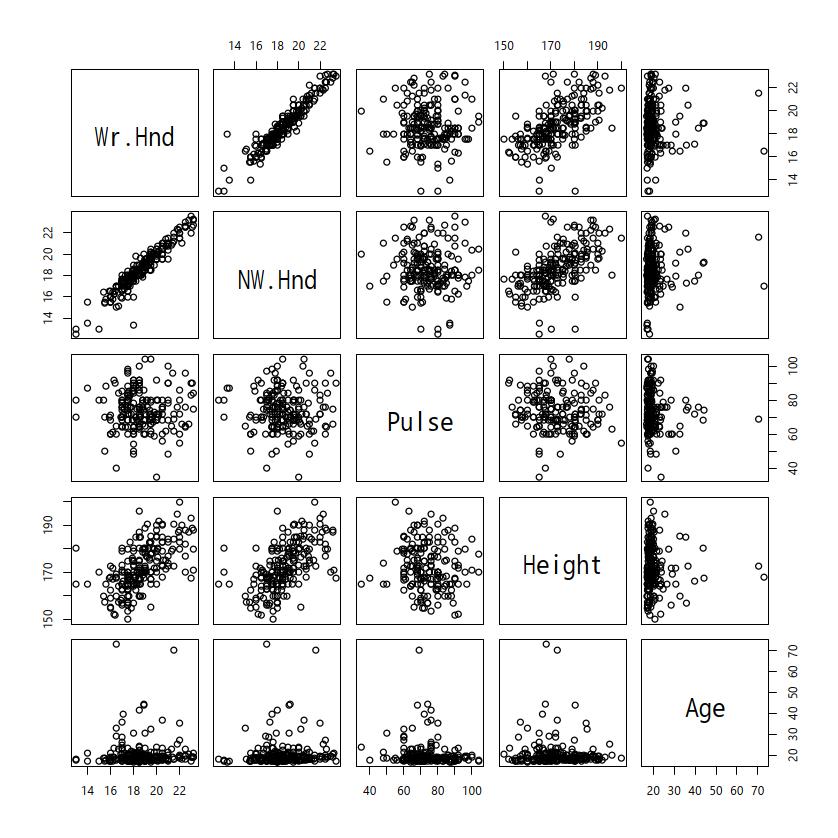
pairs()の機能が実装されている。オプション指定により,対角線上に個々の変数についてのさまざまなグラフを表示できるのが便利である。記述統計は,(1)データの特徴を把握する目的,また(2)データ入力ミスの可能性をチェックする目的で計算する。あまりにも妙な最大値や最小値,大きすぎる標準偏差などが得られた場合は,入力ミスを疑って,元データに立ち返ってみるべきである。
記述統計量には,大雑把にいって,分布の位置を示す「中心傾向」と分布の広がりを示す「ばらつき」があり,中心傾向としては平均値,中央値,最頻値がよく用いられ,ばらつきとしては分散,標準偏差,四分位範囲,四分位偏差がよく用いられる。
中心傾向の代表的なものは以下の3つである。
分布の位置を示す指標として,もっとも頻繁に用いられる。実験的仮説検証のためにデザインされた式の中でも,頻繁に用いられる。記述的な指標の1つとして,平均値は,いくつかの利点と欠点をもっている。日常生活の中でも平均をとるという操作は普通に行われるから説明不要かもしれないが,数式で書くと以下の通りである。
母集団の平均値μ(ミューと発音する)は,μ = ∑X / Nである。Xはその分布における個々の値であり,Nは値の総数である。∑(シグマと発音する)は,一群の値の和を求める記号である。すなわち,∑X = X1 + X2 + X3 + ... + XNである。
標本についての平均値を求める式も,母集団についての式と同一である。ただし,数式で使う記号が若干異なっている。標本平均X(エックスバーと発音する)は,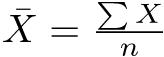 である。nは,もちろん標本サイズである53。
である。nは,もちろん標本サイズである53。
ちなみに,重み付き平均は,各々の値にある重みをかけて合計したものを,重みの合計で割った値である。重みをn1,n2,……として,各々の値をX1,X2,……として式で書くと,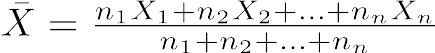
中央値は,全体の半分がその値より小さく,半分がその値より大きい,という意味で,分布の中央である。言い換えると,中央値は,頻度あるいは値の数に基づいて分布を2つに等分割する値である。中央値を求めるには式は使わない(決まった手続き=アルゴリズムとして,並べ替え(sorting)は必要)。極端な外れ値の影響を受けにくい(言い換えると,外れ値に対して頑健である)。歪んだ分布に対する最も重要なcentral tendencyの指標が中央値である。Rで中央値を計算するには,median()という関数を使う。なお,データが偶数個の場合は,普通は中央にもっとも近い2つの値を平均した値を中央値として使うことになっている。
最頻値はもっとも度数が多い値である。すべての値の出現頻度が等しい場合は,最頻値は存在しない。Rではtable(X)[which.max(table(X))]で得られる(ただし,複数の最頻値がある場合は,これだと最も小さい値しか表示されないので要注意)。
平均値は,(1)分布のすべての値を考慮した値である,(2)同じ母集団からサンプリングを繰り返した場合に一定の値となる,(3)多くの統計量や検定で使われている,という特長をもつ。標本調査値から母集団の因果関係を推論したい場合に,もっとも普通に使われる。しかし,(1)極端な外れ値の影響を受けやすい,(2)打ち切りのある分布では代表性を失う場合がある54,という欠点があり,外れ値があったり打ち切りがあったりする分布では位置の指標として中央値の方が優れている。最頻値は,標本をとったときの偶然性の影響を受けやすいし,もっとも頻度が高い値以外の情報はまったく使われない。しかし,試験の点で何点の人が多かったかを見たい場合は最頻値が役に立つし,名義尺度については最頻値しか使えない。
ここで上げた3つの他に,幾何平均(geometric mean)や調和平均(harmonic mean)も,分布の位置の指標として使われることがある。幾何平均はデータの積の累乗根(対数をとって平均値を出して元に戻したもの),調和平均はデータの逆数の平均値の逆数であり,どちらもゼロを含むデータには使えない。大きな外れ値の影響を受けにくいという利点があり,幾何平均は,とくにデータの分布が対数正規分布に近い場合によく用いられる。
一方,分布のばらつき(Variability)の指標として代表的なものは,以下の4つである。
四分位範囲について説明する前に,分位数について説明する。値を小さい方から順番に並べ替えて,4つの等しい数の群に分けたときの1/4, 2/4, 3/4にあたる値を,四分位数(quartile)という。1/4の点が第1四分位,3/4の点が第3四分位である(つまり全体の25%の値が第1四分位より小さく,全体の75%の値が第3四分位より小さい)。2/4の点というのは,ちょうど順番が真中ということだから,第2四分位は中央値に等しい。ちょっと考えればわかるように,ちょうど4等分などできない場合がもちろんあって,上から数えた場合と下から数えた場合で四分位数がずれる可能性があるが,その場合はそれらを平均するのが普通である。また,最小値,最大値に,第1四分位,第3四分位と中央値を加えた5つの値を五数要約値と呼ぶことがある(Rではfivenum()関数で五数要約値を求めることができる)。第1四分位,第2四分位,第3四分位は,それぞれQ1, Q2, Q3と略記することがある。四分位範囲とは,第3四分位と第1四分位の間隔である。上と下の極端な値を排除して,全体の中央付近の50%(つまり代表性が高いと考えられる半数)が含まれる範囲を示すことができる。
四分位範囲を2で割った値を四分位偏差と呼ぶ。もし分布が左右対称型の正規分布であれば,中央値マイナス四分位偏差から中央値プラス四分位偏差までの幅に全データの半分が含まれるという意味で,四分位偏差は重要な指標である。IQRもSIQRも少数の極端な外れ値の影響を受けにくいし,分布が歪んでいても使える指標である。
データの個々の値と平均値との差を偏差というが,マイナス側の偏差とプラス側の偏差を同等に扱うために,偏差を二乗して,その平均をとると,分散という値になる。分散Vは,
V = Σ(X - μ)2 / N
で定義される55。標本分散V(X)は,標本平均Xを使って,
V(X) = Σ (X - X)2 / n
という式で得られる。ただし,標本平均がそのまま母平均の推定値となるのに対して,標本分散は母分散の推定値にならない。母分散の推定値としては,標本サイズnで割る代わりに自由度n − 1で割って得られる不偏分散(unbiased variance)という値を用いる。即ち,不偏分散Vub(X)は,
 である(Rでは
である(Rではvar()で得られる)。
分散の平方根をとったものが標準偏差である。平均値と次元を揃える意味をもつ。不偏分散の平方根をとったものは,不偏標準偏差と呼ばれる(Rではsd()で得られる)56。もし分布が正規分布ならば,Mean±2SD57の範囲にデータの95%が含まれるという意味で,標準偏差は便利な指標である。なお,名前は似ているが,「標準誤差」はデータのばらつきでなくて,推定値のばらつきを示す値なので混同しないように注意されたい。例えば,平均値の標準誤差は,標本の不偏標準偏差を標本サイズの平方根で割れば得られるが,意味は,「もし標本抽出を何度も繰り返して行ったとしたら,得られる標本平均のばらつきは,一定の確率で標準誤差の範囲におさまる」ということである。ちなみに,データそのものがどのような分布であっても,標本抽出回数を増やしていくと,標本平均の分布は正規分布に近づくことが中心極限定理によって証明されている。例えば,区間(0, 1)の一様分布から,サイズ10の無作為標本を1000回抽出すると,その平均値の分布がほぼ正規分布していることは,以下のコードで確かめることができる。
x <- runif(10000)
y <- matrix(numeric(1000*10), 10)
for (i in 1:1000) { y[, i] <- sample(x, 10, replace=FALSE) }
hist(colMeans(y))上記の記述統計量を計算するには,Rcmdrからは,メニューバーの「統計量」の「要約」から「数値による要約」を選べばよいし,EZRでは,「統計解析」の「連続変数の解析」の「連続変数の要約」を選べばよい。選びたい変数の上にマウスカーソルを移動し,を押しながら左クリックすることで,複数の変数を選択することができる。オプションをとくに指定しなければ,平均値,標準偏差,最小値,第1四分位(25パーセンタイル),中央値(50パーセンタイル),第3四分位(75パーセンタイル),最大値,有効標本サイズ,欠損値の数が,選択した変数すべてについて表示される。
分布の正規性の検定は,コルモゴロフ=スミルノフ検定あるいはシャピロ=ウィルク検定が有名である。fmsbパッケージにはギアリーの検定も実装してある。もちろん検定をする前に,ヒストグラムか正規確率プロットによって分布の様子を確認しておくことは必須である。例えば,surveyデータフレームに含まれているNW.Hndという変数(利き手でない方の手を開いたときの親指と小指の先の距離)について分布の正規性の検定を行うには以下のように打つ。
mu <- mean(survey$NW.Hnd[!is.na(survey$NW.Hnd)])
psd <- sd(survey$NW.Hnd[!is.na(survey$NW.Hnd)])
ks.test(survey$NW.Hnd, "pnorm", mean=mu, sd=psd)
shapiro.test(survey$NW.Hnd)EZRでは,「統計解析」の「連続変数の解析」の「正規性の検定」を選び,変数としてNW.Hndを選んでOKボタンをクリックするだけでできる。自動的にコルモゴロフ=スミルノフ検定の(サンプルサイズが5000以下のときはシャピロ=ウィルク検定も)結果が表示され,ヒストグラムに正規分布を重ね描きしたグラフも作成される。コルモゴロフ=スミルノフ検定とシャピロ=ウィルク検定の結果が異なることがあるが,これらの検定は分布の正規性へのアプローチが異なるので,結果が一致しないこともある。また,多くの検定手法がデータの分布の正規性を仮定しているが,これらの検定で正規性が棄却されたからといって機械的に変数変換やノンパラメトリック検定でなくてはいけないとは限らない。独立2標本の平均値の差がないという仮説を検定するためのt検定(等分散性を仮定しないWelchの方法も含めて)は頑健な手法なので,正規分布に従っているといえなくても,そのまま実行してもいい場合も多い。ただし,明らかな外れ値がある場合は検出力が落ちるので,Wilcoxonの順位和検定のようなノンパラメトリックな検定の方が良い場合もある。
外れ値についても,グラフで確認することは必須である。統計学的に有意に正規分布から外れているかどうかの検定にも何種類かあるが,スミルノフ=グラブス検定は,outliersパッケージに含まれているgrubbs.test()関数や群馬大学の青木繁伸教授がwebサイトで提供しているSG()関数58によって実行可能である。
EZRでは,「統計解析」の「連続変数の解析」の「外れ値の検定」を選んで,変数としてNW.Hndを指定してOKボタンをクリックするだけでいい。外れ値をNAで置き換えた新しい変数を作成することも右のオプション指定から容易にできる。有意な外れ値がない場合は,“No outliers were identified.”と表示されるが,既に書いた通り,この結果だけで機械的に外れ値を除外することはお薦めできない。
ばらつきとは別に、データの分布の形を示す記述統計量として、尖度(kurtosis)と歪度(skewness)が使われる。これらはR本体には関数として実装されていないが、e1071パッケージに入っている。そのhelpによると、Joanes and Gill (1988)に基づいて、それぞれ3通りの計算方法が実装されており、オプションとして指定できる。
古典的定義(歪度を3次のモーメントを2次のモーメントの平方根の3乗で割った値、尖度を4次のモーメントを2次のモーメントの二乗で割って3を引いた値とする定義。ちなみにr次のモーメントとは平均からの偏差のr乗和をサンプルサイズで割った値である)に基づくのがtype=1で、SASやSPSSと同じ実装がtype=2(e1071パッケージのヘルプでは表示されないが、Joanes and Gill, 1988によると、EXCELもこの実装を採用しているとのこと)、MINITABやBMDPと同じ実装がtype=3で、どちらもデフォルトはtype=3とのこと。
正規分布の下で不偏推定量であることがわかっているのは、歪度の方は3つともだが、尖度はtype=2だけとのことなので(なぜtype=2をデフォルトにしなかったのか謎だが)、R本体でlibrary(e1071)からskewness()やkurtosis()を使う場合は、特別な理由がない限り、type=2を指定すべきであろう。
EZRでは統計解析>連続変数の解析>正規性の検定でアウトプットウィンドウの中に表示されるが、type=2の結果と同じようだ。
jamoviは探索(Exploration)の記述統計(Descriptives)で変数を選んで計算させた後で統計量(Statistics)の分布(Distribution)の下にある歪度(skewness)と尖度(kurtosis)にチェックを入れるとtype=2と同じ結果が表示される。
医学統計ではSASやSPSSと同じ結果になるのが無難な選択であろうから、EZRの方針は合理的だと思う。元々心理統計のために開発されたらしいjamoviも、最近は医学論文でも使われているから、妥当な選択であろう。
なお、EZRやjamoviでは欠損値があっても自動的に除去して計算してくれるが、e1071パッケージのskewness()やkurtosis()は標準関数のmean()やvar()と同じく、na.rm=FALSEオプションがデフォルトなので、欠損値が含まれていると結果がNAになる。欠損値を除去して計算させたい場合は、na.rm=TRUEというオプション指定も必要である。
論文を書く場合,結果の最初にTable 1としてサンプルの基本属性の集計結果をまとめて表示することが多い。EZRは,バージョンアップによって,この機能を内蔵するようになった。メニューの「グラフと表」の「サンプルの背景データのサマリー表の出力」を選び,群別する変数(0~1つ選択),カテゴリー変数(名義変数、順序変数),連続変数(正規分布),連測変数(非正規分布)59を選び,正規分布しない連続変数の範囲表示をデフォルトの「最小値と最大値」にするのか「四分位範囲(Q1-Q3)」にするのかを選んでから「OK」をクリックする。
cranにはtable1というパッケージが存在し,名前の通り,Table 1を見やすく作るための機能を提供している。詳細はhttps://cran.r-project.org/web/packages/table1/vignettes/table1-examples.htmlに説明されている。同じ目的でtableoneというパッケージも存在し,https://cran.r-project.org/web/packages/tableone/vignettes/introduction.htmlに使い方が説明されている。他にもたくさんのパッケージが似た目的で開発されており,比較記事60が書かれていて参考になる。
医学統計でよく使われるのは,伝統的に仮説検定である。仮説検定は,意味合いからすれば,元のデータに含まれる情報量を,仮説が棄却されるかどうかという2値情報にまで集約してしまうことになる。これは情報量を減らしすぎであって,点推定量と信頼区間を示す方がずっと合理的なのだが,伝統的な好みの問題なので,この演習でも検定を中心に説明する。もっとも,RothmanとかGreenlandといった最先端の疫学者は,仮説検定よりも区間推定,区間推定よりもp値関数の図示(リスク比やオッズ比については,fmsbパッケージにpvalueplot()関数として実装済み)の方が遥かによい統計解析であると断言している。
最も単純な検定の1つは,独立2標本間の分布の位置の差の検定であり,非常によく使われているので,まずはここから検定の考え方を見てみよう。
典型的な例として,独立にサンプリングされた2群の平均値の差がないという帰無仮説の検定を考えよう。通常,研究者は,予め,検定の有意水準を決めておかねばならない。検定の有意水準とは,間違って帰無仮説が棄却されてしまう確率が,その値より大きくないよう定められるものである。ここで2つの考え方がある。フィッシャー流の考え方では,p値(有意確率)は,観察されたデータあるいはもっと極端なデータについて帰無仮説が成り立つ条件付き確率である。もし得られたp値が小さかったら,帰無仮説が誤っているか,普通でないことが起こったと解釈される。ネイマン=ピアソン流の考え方では,帰無仮説と対立仮説の両方を定義しなくてはならず,研究者は繰り返しサンプリングを行ったときに得られる,この手続きの性質を調べる。即ち,本当は帰無仮説が正しくて棄却されるべきではないのに誤って棄却するという決断をしてしまう確率(これは「偽陽性」あるいは第一種の過誤と呼ばれる)と,本当は誤っている帰無仮説を誤って採択してしまう確率(第二種の過誤と呼ばれる)の両方を調べる。これら2つの考え方は混同してはならず,厳密に区別すべきである。
通常,有意水準は0.05とか0.01にする。上述の通り,検定の前に決めておくべきである。得られた有意確率がこの値より小さいとき,統計的な有意性があると考えて帰無仮説を棄却する。
独立2群間の統計的仮説検定の方法は,以下のようにまとめられる。
shapiro.test()でShapiro-Wilkの検定ができるが,その結果を機械的に適用して判断すべきではない):Welchの検定(Rではt.test(x,y))61wilcox.test(x,y))が標準的に使われてきたが(Mann-WhitneyのU検定という言い方もあるが,数学的にまったく同じ検定である),これらは分布の形は仮定しないけれども,2群が連続分布であることと,分布の形に差がない「ズレのモデル」を前提としているため,それさえも仮定しない,Brunner-Munzel検定が最近提案され,広まりつつある。prop.test())。次章で扱う。標本調査によって得られた独立した2つの量的変数XとY(サンプルサイズが各々nXとnYとする)の比較を考える。
2つの量的変数XとYの不偏分散SX<-var(X)とSY<-var(Y)の大きい方を小さい方で(以下の説明ではSX>SYだったとする)割ったF0<-SX/SYが第1自由度DFX<-length(X)-1,第2自由度DFY<-length(Y)-1のF分布に従うことを使って検定する。有意確率は1-pf(F0,DFX,DFY)で得られる。しかし,F0を手計算しなくても,var.test(X,Y)で等分散かどうかの検定が実行できる。また,1つの量的変数Xと1つの群分け変数Cがあって,Cの2群間でXの分散が等しいかどうか検定するというスタイルでデータを入力してある場合は,var.test(X~C)とすればよい。
この結果,2群間で分散が統計的に有意に異なっていたら,その情報自体が,異なる母集団からのサンプルであるとか,サンプリングが偏っていた可能性を示唆する。かつては,等分散性の検定結果によって平均値の差のt検定において等分散性を仮定したりWelchの方法にしたりといったことをしていたが,現在では,等分散と考えられるかどうかによらず,Welchの方法で検定すれば良い。
Rcmdrでは「統計量」の「分散」から「分散の比のF検定」を選び,グループ(Group variable)としてCを,目的変数(Response variable)としてXを選ぶ。ただし,グループ変数は要因型になっていないと候補として表示されないので,もし0/1で入力されていたら,予め「データ」の「アクティブデータセット内の変数の操作」で「数値変数を因子に変換」を用いて要因型にしておく(字面は0/1のままでもOK)。surveyデータで,「男女間で身長の分散に差がない」という帰無仮説を検定するには,グループとしてSexを,目的変数としてHeightを選んで[OK]ボタンをクリックする。デフォルトでは両側検定されるが,仮説によっては片側検定をすることもあり,その場合は「対立仮説」の下のラジオボタンのチェックを変えればいい。男女それぞれの分散と,検定結果が「出力ウィンドウ」に表示される。
EZRでは,「統計解析」の「連続変数の解析」から「2群の等分散性の検定(F検定)」を選び,目的変数(1つ選択)の枠からXを,グループ(1つ選択)の枠からCを選び(EZRでは要因型にしなくても選べる), OKボタンをクリックする。surveyデータで,「男女間で身長の分散に差がない」という帰無仮説を検定するには,目的変数としてHeightを,グループとしてSexを選び,OKボタンをクリックすると,男女それぞれの分散と検定結果がOutputウィンドウに表示される。
 が自由度ϕのt分布に従うことを使って検定する。但し,ϕは下式による。
が自由度ϕのt分布に従うことを使って検定する。但し,ϕは下式による。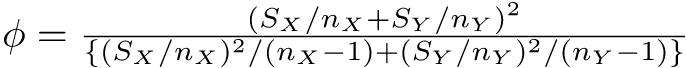
Rでは,t.test(X,Y,var.equal=F)だが,var.equalの指定を省略した時は等分散でないと仮定してWelchの検定がなされるので省略してt.test(X,Y)でいい。量的変数Xと群分け変数Cという入力の仕方の場合は,t.test(X~C)とする62。surveyデータで「男女間で平均身長に差がない」という帰無仮説を検定したいときは,t.test(Height ~ Sex, data=survey)とする。
なお,t検定の効果量については,第5章「研究のデザイン」で既に述べたので,そちらを参照されたい。
Rcmdrでは「統計量」の「平均値」の「独立サンプルt検定」を選んで,グループ(Group variable)としてCを,目的変数(Response variable)としてXを選んで,等分散と考えますか? というラジオボタンは「No」にしておき,両側検定か片側検定かを選んでから[OK]ボタンをクリックする。ただし,グループ変数は要因型になっていないと候補として表示されないので,もし0/1で入力されていたら,予め「データ」の「アクティブデータセット内の変数の管理」で「数値変数を因子に変換」を用いて要因型にしておく(字面は0/1のままでもOK。具体的には下の例題を参照)。surveyデータで「男女間で平均身長に差がない」という帰無仮説を検定したいときは,グループとしてSexを,目的変数としてHeightを選べばよい。Welchの方法による2標本t検定の結果が「出力ウィンドウ」に表示される。
EZRの場合は「統計解析」「連続変数の解析」から「2群間の平均値の比較(t検定)」を選び,目的変数としてHeightを,比較する群としてSexを選び,「等分散と考えますか?」の下のラジオボタンを「No (Welch test)」の方をチェックして,「OK」ボタンをクリックすると,結果がOutputウィンドウに表示される。男女それぞれの平均,不偏標準偏差と検定結果のp値が示され,エラーバーが上下に付いた平均値を黒丸でプロットし,それを直線で結んだグラフも自動的に描かれる。
ちなみに,surveyデータで年齢(Age)に性差があるかどうかを検定したい場合にWelchのt検定をすると,年齢は明らかに正規分布から大きく外れており,かつ外れ値が多いので検出力が落ちる。実際にやってみるとわかるが有意でない。
なお,既に平均値と不偏標準偏差が計算されている場合の図示は,エラーバー付きの棒グラフがよく使われるが(barplot()関数で棒グラフを描画してから,arrows()関数でエラーバーを付ければよい),棒グラフを描く時は基線をゼロにしなくてはいけないことに注意されたい。生データがあれば,stripchart()関数を用いて,生データのストリップチャートを描き,その脇に平均値とエラーバーを付け足す方がよい。そのためには,量的変数と群別変数という形にしなくてはいけないので,たとえば,2つの量的変数V <- rnorm(100,10,2)とW <- rnorm(60,12,3)があったら,予め
X <- c(V, W)
C <- as.factor(c(rep("V", length(V)), rep("W", length(W))))
x <- data.frame(X, C)または
x <- stack(list(V=V, W=W))
names(x) <- c("X", "C")のように変換しておく必要がある63。プロットするには次のように入力すればよい64。
stripchart(X~C, data=x, method="jitter", vert=TRUE)
Mx <- tapply(x$X, x$C, mean)
Sx <- tapply(x$X, x$C, sd)
Ix <- c(1.1, 2.1)
points(Ix, Mx, pch=18, cex=2)
arrows(Ix, Mx-Sx, Ix, Mx+Sx, angle=90, code=3)各対象について2つずつの値があるときは,それらを独立2標本とみなすよりも,対応のある2標本とみなす方が切れ味がよい。全体の平均に差があるかないかだけをみるのではなく,個人ごとの違いを見るほうが情報量が失われないのは当然である。
対応のある2標本の差の検定は,paired-t検定と呼ばれ,意味合いとしてはペア間の値の差を計算して値の差の母平均が0であるかどうかを調べることになる。Rで対応のある変数XとYのpaired-t検定をするには,t.test(X,Y,paired=T)で実行できるし,それはt.test(X-Y,mu=0)と等価である。
surveyデータで「親指と小指の間隔が利き手とそうでない手の間で差がない」という帰無仮説を検定するには,Rコンソールでは,
t.test(survey$Wr.Hnd, survey$NW.Hnd, paired=TRUE)と打てばよい。グラフは通常,同じ人のデータは線で結ぶので,例えば次のように打てば,差が1 cm以内の人は黒,利き手が1 cm以上非利き手より大きい人は赤,利き手が1 cm以上非利き手より小さい人は緑で,人数分の線分が描かれる。
Diff.Hnd <- survey$Wr.Hnd - survey$NW.Hnd
C.Hnd <- ifelse(abs(Diff.Hnd)<1, 1, ifelse(Diff.Hnd>0, 2, 3))
matplot(rbind(survey$Wr.Hnd, survey$NW.Hnd), type="l",
lty=1, col=C.Hnd, xaxt="n")
axis(1, 1:2, c("Wr.Hnd", "NW.Hnd"))
Rcmdrでは「統計量」の「平均」の「対応のあるt検定」を選ぶ(EZRでは「統計解析」「連続変数の解析」から「対応のある2群間の平均値の検定(paired t検定)」を選ぶ)。第1の変数としてWr.Hndを,第2の変数としてNW.Hndを選び,[OK]ボタンをクリックすると,出力ウィンドウ(EZRではOutputウィンドウ)に結果が得られる。有意水準5%で帰無仮説は棄却され,利き手の方がそうでない手よりも親指と小指の間隔が有意に広いといえる。
なお,対応のあるt検定の意味を考えれば,EZRでも「アクティブデータセット>変数の操作>計算式を入力して新たな変数を作成する」として,新しい変数名としてDiff.Hndとして,計算式としてWr.Hnd-NW.HndとしてOKをクリックすることで手の大きさの差の変数を作り,このDiff.Hndの母平均がゼロかどうかを「統計解析>連続変数の解析>1標本の平均値のt検定」で検定することもできる。その場合は結果として差の期待値と信頼区間が得られる。
例題
Rcmdrのメニューで「データ」の「パッケージ内のデータ」の「アタッチされたパッケージからデータセットを読み込む」(EZRでは「ファイル」「パッケージに含まれるデータを読み込む」)を選び,左側からdatasetsパッケージをダブルクリックし,右側からinfertデータフレームをダブルクリックすると,Trichopoulos et al. (1976) Induced abortion ans secondary infertility. Br J Obst Gynaec, 83: 645-650.で使われているデータを読み込むことができる。
アテネ大学の第一産婦人科を受診した続発性の不妊の100人の女性の1人ずつについて同じ病院から年齢,既往出生児数,教育歴をマッチングした健康な(不妊でない)女性2人ずつを対照として選ぶことを目指してサンプリングし,2人の対照が見つかった不妊患者が83人だったので,この患者と対照全員を含むデータである(ただし74組目だけ対照が1人しかデータに含まれていないので,249人でなく248人のデータとなっている。除かれたのはそれまでの自然流産と人工妊娠中絶が2回ずつあった人である)。
含まれている変数は以下の通りである。
education: 教育を受けた年数(3水準の要因型)
age: 年齢
parity: 既往出生児数
induced: それまでの人工妊娠中絶回数(2は2回以上)
case: 不妊の女性が1,対照が0
spontaneous: それまでの自然流産回数(2は2回以上)
stratum: マッチングした組の番号
pooled.stratum: プールした層番号(1) 不妊患者と対照の間で自然流産を経験した数に差がないという帰無仮説を検定せよ。(2)各女性の自然流産の経験数と人工妊娠中絶の経験数に差がないという帰無仮説を検定せよ。有意水準はともに5%とする。
本当は因果を逆に考えてロジスティック回帰またはポアソン回帰する方が筋がいいと思うが,ここでは敢えて平均値の差の検定をしてみる。2群間で分布が異なるし対照群では正規分布から明らかに外れているが,それにも目をつぶって平均値の差の検定を行う。2回以上というのを2回と扱っていいのかという点にも問題があるが,ここでは目をつぶる。Rコンソールでは,この操作は単純である。必要なt検定をするには,次のように打てば良い。
t.test(spontaneous ~ case, data=infert)とする。もし患者群と対照群の間で分散が等しいという帰無仮説を検定したいときは,
var.test(spontaneous ~ case, data=infert)t.test(infert$induced, infert$spontaneous, paired=TRUE)Rcmdrで群別に分布をみるには,群分け変数が要因型でなくてはならないので,まず「データ」の「アクティブデータセット内の変数の管理」の「数値変数を因子に変換」でcaseを因子型に変えておく。変数としてcaseを選び,因子水準は「水準名を指定」がチェックされた状態にして,新しい変数または複数の変数に対する接頭文字列のところが<変数と同じ>となっているのをgroupとして(ここは,複数の数値型変数を一度に因子型に変換するときは接頭文字列を入力するが,1つだけの場合は新しい変数名全体を打つ必要がある),因子型の変数名がgroupとなるように指定する。すると水準名を指定するウィンドウが開くので,0のところにcontrol,1のところにinfertileと打つ。そうやって準備をしておいてから,「グラフ」の「箱ひげ図」で「変数(1つを選択)」としてspontaneousを選び,「層別のプロット」ボタンをクリックして「層別変数(1つ選択)」としてgroupを選ぶと,対照群と不妊群別々に箱ひげ図を描くことができる。値が0, 1, 2しかないので箱ひげ図よりも棒グラフあるいはヒストグラムの方がわかりやすいが,棒グラフやヒストグラムはRcmdrでは層別でプロットできないため,ここでは箱ひげ図を採用した。もちろん「平均のプロット」で標準偏差をエラーバーとする平均値を線で結んだプロットをさせてもよい。
(1) 「統計量」の「平均」の「独立サンプルt検定」を選び(EZRでは「統計解析」「連続変数の解析」から「2群間の平均値の比較(t検定)」を選び),「等分散と考えますか?」で「No」にチェックが入っていることを確認し,グループをgroup,目的変数をspontaneousにして[OK]をクリックするとWelchの方法によるt検定が実行できる(なお,「統計量」の「分散」の「分散の比のF検定」でグループをgroup,目的変数をspontaneousとして両側検定を実行すると出力ウィンドウに表示されるp-valueが小さいので,2群の分散にも統計的な有意差があることがわかる)。
(2) 「統計量」の「平均」の「対応のあるt検定」を指定し(EZRなら「統計解析」「連続変数の解析」から「対応のある2群間の平均値の検定(paired t検定)」を選ぶ),第1の変数としてspontaneous,第2の変数としてinducedを選んで[OK]ボタンをクリックすれば実行できる。
Wilcoxonの順位和検定は,パラメトリックな検定でいえば,t検定を使うような状況,つまり,独立2標本の分布の位置に差がないかどうかを調べるために用いられる。Mann-WhitneyのU検定と(これら2つほど有名ではないが,KendallのS検定とも)数学的に等価である。Rcmdrでは,「統計量」の「ノンパラメトリック検定」を選んで実行する。
データがもつ情報の中で,単調変換に対して頑健なのは順位なので,これを使って検定しようという発想である。以下,Wilcoxonの順位和検定の手順を箇条書きする。
例として,surveyデータで,身長(Height)の分布の位置が男女間で差がないという帰無仮説を検定してみよう。
Rコンソールでは簡単で,library(MASS)してあれば,
> wilcox.test(Height ~ Sex, data=survey)だけで良い。
Wilcoxonの順位和検定の効果量については,https://core.ecu.edu/wuenschk/docs30/Nonparametric-EffectSize.pdfで説明されているように,p値からZ値を求めて(両側検定のp値から求める場合は2で割ることを忘れないように)サンプルサイズの平方根で割るという正規近似による方法と,effectsizeパッケージを使ってrank_biserial()関数を使う方法が知られている(得られる効果量はCliff's deltaといい,負の値も取り得るが,絶対値を解釈すれば良い)。この効果量rは,https://cran.r-project.org/web/packages/statsExpressions/vignettes/stats_details.htmlに書かれているように,0.1-0.3で小さい,0.3-0.5で中程度,0.5以上で大きいと判断するのが目安である。上記の例であれば,コードは以下。
> library(MASS)
> res <- wilcox.test(Height ~ Sex, data=survey)
> abs(qnorm(res$p.value/2))/sqrt(sum(complete.cases(survey[,c("Height", "Sex")])))
> library(effectsize)
> rank_biserial(Height ~ Sex, data=survey)Rcmdrでは「統計量」の「ノンパラメトリック検定」で「2標本ウィルコクソン検定」を選び,グループ変数としてSexを選び,応答変数としてHeightを選んで[OK]ボタンをクリックする。
EZRでは「統計解析」「ノンパラメトリック検定」から「2群間の比較(Mann-Whitney U検定)」を選び,目的変数としてHeightを,比較する群としてSexを選んで「OK」ボタンをクリックする。検定結果がOutputウィンドウに表示されるだけでなく,箱ひげ図も同時に描かれる。身長の性差の検定結果はWelchのt検定と同じく有意差があるといえる。
同じsurveyデータフレームで年齢(Age)に性差があるかどうかについては,Welchのt検定では有意でなかったが,Wilcoxonの順位和検定をすると5%水準で有意である。これはAgeの分布が大きく右裾を引いた歪んだ分布になっていて,しかも外れ値が多いため,Welchのt検定の検出力が低くなっているためである。
詳しくは,web上の三重大学奥村晴彦教授の解説記事65やhoxo_mさんの解説記事66を参照されると良いと思うが,「独立2群から一つずつ値を取り出したとき,どちらが大きい確率も等しい」という帰無仮説を検定するために67,BrunnerとMunzelが提案した比較的新しい方法である。残念ながら現在のところEZRには入っていない。
元論文は,Brunner E, Munzel U (2000) The nonparametric Behrens-Fisher problem: Asymptotic theory and a small-sample approximation. Biometrical Journal, 42: 17-25.であり,Rでは,lawstatパッケージのbrunner.munzel.test()で実行できる(使うためには,予めinstall.packages("lawstat", dep=TRUE)により,各種依存パッケージとともにlawstatパッケージをインストールしておく必要がある)。
上の例と同様に,MASSパッケージに入っているsurveyデータで,身長の分布の位置が男女で差がないという帰無仮説をBrunner-Munzel検定するには,
> library(lawstat)
> HT <- tapply(survey$Height,survey$Sex,print)
> brunner.munzel.test(HT$Male,HT$Female)とすれば良い。下枠内の結果が得られる。Ageについても同様に計算できるので確かめられたい。
Brunner-Munzel Test
data: HT$Male and HT$Female
Brunner-Munzel Test Statistic = -17.6824, df = 157.29, p-value < 2.2e-16
95 percent confidence interval:
0.0615193 0.1496350
sample estimates:
P(X<Y)+.5*P(X=Y)
0.1055771なお,サンプルサイズが極めて小さい場合は,Neubert K, Brunner E (2007) A studentized permutation test for the non-parametric Behrens-Fisher problem. Computational Statistics and Data Analysis, 51: 5192-5204.に示されているように,Brunner-Munzel統計量に並べ替え検定を適用すれば良いが(前掲した三重大学奥村晴彦教授の解説記事にコードが示されている),相当な計算時間がかかる。
最近開発された,brunnermunzelパッケージのbrunnermunzel.test()関数のperm=TRUEオプションを使えば(強引にさせたい場合はforce=TRUEオプションもつければ),高速な並べ替え検定が可能であるが,欠損値が含まれているとエラーが出るので,予め欠損値のないsubsetにしておくか,多重代入法などで欠損値を推定してから適用し結果を統合するという面倒なプロセスを踏まねばならないし,サンプルサイズが大きい場合もエラーが出て計算できない。
install.packages("brunnermunzel", dep=TRUE)によってbrunnermunzelパッケージをインストールした後,以下のコードを実行するとBrunner-Munzel検定ができるが,サンプルサイズが大きすぎて並べ替え検定の結果は得られない。
> library(brunnermunzel)
> mHT <- subset(survey, !is.na(Height)&Sex=="Male")$Height
> fHT <- subset(survey, !is.na(Height)&Sex=="Female")$Height
> brunnermunzel.test(mHT, fHT, perm=FALSE)
> brunnermunzel.test(mHT, fHT, perm=TRUE, force=TRUE) # エラーになるそこで,2種類の催眠剤(group)を10人の被験者(ID)に使った場合の睡眠時間増加(extra)データであるsleepを使って試すには(このデータは同じ人の2回の測定値であり,対応があるため,Brunner-Munzel検定には向いていないが,適当なサンプルサイズであるため使ってみた)以下の通り。
d1sleepextra <- subset(sleep, group=="1")$extra
d2sleepextra <- subset(sleep, group=="2")$extra
brunnermunzel.test(d1sleepextra, d2sleepextra, perm=FALSE)
brunnermunzel.test(d1sleepextra, d2sleepextra, perm=TRUE, force=TRUE)この結果のp値をみると,近似的な検定では0.04682と5%水準では有意だが,並べ替え検定では0.05513と有意でない。
Wilcoxonの符号付き順位検定は,対応のあるt検定のノンパラメトリック版である。ここでは説明しないが,多くの統計学の教科書に載っている。
実例だけ出しておく。surveyデータには,利き手の大きさ(親指と小指の先端の距離)を意味するWr.Hndという変数と,利き手でない方の大きさを意味するNW.Hndという変数が含まれているので,これらの分布の位置に差が無いという帰無仮説を有意水準5%で検定してみよう。
同じ人について利き手と利き手でない方の手の両方のデータがあるので対応のある検定が可能になる。Rコンソールでは,
> wilcox.test(survey$Wr.Hnd, survey$NW.Hnd, paired=TRUE)とすればよい。
Rcmdrでは,「統計量」,「ノンパラメトリック検定」,「対応のあるウィルコクソン検定」と選択し(EZRでは,「統計解析」「ノンパラメトリック検定」から「対応のある2群間の比較(Wilcoxonの符号付き順位和検定)」を選び),第1の変数として左側のリストからWr.Hndを選び,第2の変数として右側のリストからNW.Hndを選んで[OK]ボタンをクリックするだけである。順位和検定のときと同じく検定方法のオプションを指定できるが,通常はデフォルトで問題ない。
ちなみに,この検定結果はp=0.0825となり,5%水準で有意でない。対応のあるt検定では有意だったのにこうなるのは,データが正規分布に近い分布である場合には,t検定の方が検出力が大きいためである。Diff.Hndは分布の正規性の検定をするとShapiro-Wilkの検定で5%水準で有意に正規分布と差があるけれども(1人だけある外れ値を除外しても有意差あり),外れ値を除外してヒストグラムを描くと正規分布に近いように見える。こういう場合は,一般にt検定の方が検出力が高い。
食物摂取頻度調査の結果のように,頻度を順序尺度で示すデータについて,独立2群間での比較をしたい場合,(1)各頻度カテゴリを1つの数値で代表させ,量として扱うことでt検定する,(2)順序なのでWilcoxonの順位和検定(Mann-WhitneyのU検定)を行う,(3)順序の情報を無視してカテゴリとしてカイ二乗検定する,といった方法が良く行われているが,(1)は代表のさせ方が妥当である保証がなく,(2)は同順位が多くなると考えられるため正しいp値が得られない可能性が高く,(3)は順序の情報を捨ててしまうため検出力が下がるという問題がある。
このような場合,グループで順序を説明するという順序ロジスティック回帰と,定数で順序を説明する(つまり順序間に差が無い)という順序ロジスティック回帰の結果の尤度比をとり,尤度比検定をすることができる。EZRのメニューにはないが,以下に例を示す。yが6段階の順序尺度をもつ変数で,xがAとBの2群を示す変数である。
set.seed(123)
y1 <- c(sample(1:3, 20, rep=TRUE), sample(4:6, 30, rep=TRUE))
y2 <- c(sample(1:3, 30, rep=TRUE), sample(4:6, 20, rep=TRUE))
y <- as.ordered(c(y1, y2))
x <- as.factor(c(rep("A", 50), rep("B", 50)))
table(y, x)
library(MASS) # polr()関数を使うので
anova(polr(y ~ x), polr(y ~ 1)) # 尤度比検定
chisq.test(table(y, x)) # カイ二乗検定でもやってみる以下の結果が得られる。カイ二乗検定では順序の情報をまったく使わないので検出力が低く,xとyの独立性は棄却されないが,尤度比検定ではxの2群間で,yの値に,5%水準で有意な差があるといえる。
> table(y, x)
x
y A B
1 5 12
2 7 10
3 8 8
4 11 5
5 8 7
6 11 8
> anova(polr(y ~ x), polr(y ~ 1)) # 尤度比検定
Likelihood ratio tests of ordinal regression models
Response: y
Model Resid. df Resid. Dev Test Df LR stat. Pr(Chi)
1 1 95 357.7997
2 x 94 353.9071 1 vs 2 1 3.892613 0.04849892
> chisq.test(table(y, x)) # カイ二乗検定でもやってみる
Pearson's Chi-squared test
data: table(y, x)
X-squared = 6.2021, df = 5, p-value = 0.287
2つのカテゴリ変数間の関係としては,独立かどうか,独立でないとしたらどの程度の関連があるかを調べることになるが,2つのカテゴリ変数の関係が独立であるという帰無仮説は,第1のカテゴリ変数で示されるグループ間で,第2のカテゴリ変数で示される構成比に差がないという帰無仮説と同等である。これらのカテゴリ変数がともに2値変数である場合は,これは2群の母比率の差の検定に帰着する。
たとえば,患者群n1名と対照群n2名の間で,ある特性をもつ者の人数がそれぞれr1名とr2名だったとして,その特性の母比率に差がないという帰無仮説を考える。
2群の母比率p1とp2が,各々の標本比率p̂1 = r1 / n1及びp̂2 = r2 / n2として推定されるとき,それらの差を考える。差(p̂1 - p̂2)の平均値と分散は,E(p̂1 - p̂2) = p1 - p2V(p̂1 - p̂2) = p1(1 - p1) / n1 + p2(1 - p2) / n2となる。
2つの母比率に差が無いならば,p1 = p2 = pとおけるはずなので,V(p1 - p2) = p(1 - p)(1 / n1 + 1 / n2)となる。
このpの推定値として,p̂ = (r1 + r2)/(n1 + n2)を使い,q̂ = 1 − p̂とおけば,n1p1とn2p2がともに5より大きければ,標準化して正規近似を使い,
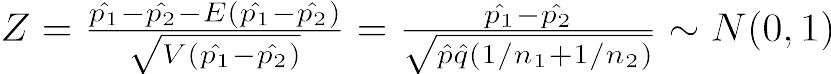 によって検定できる。即ち,このZは離散値しかとれないため,連続分布である正規分布による近似の精度を上げるために,連続性の補正と呼ばれる操作を加え,かつp1 > p2の場合(つまりZ > 0の場合)とp1 < p2の場合(つまりZ < 0の場合)と両方考える必要があり,正規分布の対称性から絶対値をとってZ > 0の場合だけ考え,有意確率を2倍する。即ち,
によって検定できる。即ち,このZは離散値しかとれないため,連続分布である正規分布による近似の精度を上げるために,連続性の補正と呼ばれる操作を加え,かつp1 > p2の場合(つまりZ > 0の場合)とp1 < p2の場合(つまりZ < 0の場合)と両方考える必要があり,正規分布の対称性から絶対値をとってZ > 0の場合だけ考え,有意確率を2倍する。即ち,
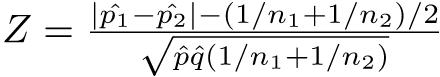 として,このZの値が標準正規分布の97.5%点(Rならば
として,このZの値が標準正規分布の97.5%点(Rならばqnorm(0.975, 0, 1))より大きければ有意水準5%で帰無仮説を棄却する。
数値計算をしてみるため,仮に,患者群100名と対照群100名で,喫煙者がそれぞれ40名,20名だったとする。喫煙率に2群間で差がないという帰無仮説を検定するには,
> p <- (40+20)/(100+100)
> q <- 1-p
> Z <- (abs(40/100-20/100)-(1/100+1/100)/2)/sqrt(p*q*(1/100+1/100))
> 2*(1-pnorm(Z))より,有意確率が約0.0034となるので,有意水準5%で帰無仮説は棄却される。つまり,喫煙率に2群間で差がないとはいえないことになる。
差の95%信頼区間を求めるには,サンプルサイズが大きければ正規分布を仮定できるので,原則どおりに差から分散の平方根の1.96倍を引いた値を下限,足した値を上限とすればよい。この例では,
> dif <- 40/100-20/100
> vardif <- 40/100*(1-40/100)/100+20/100*(1-20/100)/100
> difL <- dif - qnorm(0.975)*sqrt(vardif)
> difU <- dif + qnorm(0.975)*sqrt(vardif)
> cat("喫煙率の差の点推定値=", dif, " 95%信頼区間= [",difL,",",difU,"]\n")より,[0.076, 0.324]となる。しかし,通常は連続性の補正を行うので,下限からはさらに(1/n1 + 1/n2)/2 = (1/100 + 1/100)/2 = 0.01を引き,上限には同じ値を加えて,95%信頼区間は[0.066, 0.334]となる。
Rには,こうした比率の差を検定するための関数prop.test()が用意されており,以下のように簡単に実行することができる。
> smoker <- c(40, 20)
> pop <- c(100, 100)
> prop.test(smoker, pop)母比率の推定と,2群間でその差がないという帰無仮説の検定68,差の95%信頼区間を一気に出力してくれる。surveyデータフレームで「利き手が左である割合に男女で差が無い」という帰無仮説を検定するには,
> prop.test(table(survey$Sex, survey$W.Hnd))とすれば良い。
Rcmdrでは,「統計量」の「比率」から「2標本の比率の検定」を選ぶ。surveyデータフレームで,「利き手が左である割合に男女で差がない」という帰無仮説を検定するには,グループとしてSex,目的変数としてW.Hndを指定し,検定のタイプとして「連続修正を用いた正規近似」にチェックを入れて[OK]ボタンをクリックすればよい。
EZRでは,「統計解析」「名義変数の解析」から「分割表の作成と群間の比率の比較」を選ぶ。この例では,行の選択の枠からSex,列の変数の枠からW.Hndを選び,「仮説検定」のなかから「カイ2乗検定」の左のボックスにチェックを入れ,「カイ2乗検定の連続性補正」の下のラジオボタンを「はい」にして「OK」ボタンをクリックする。
2つのカテゴリ変数の関係を考えるとき,一般に,もっともよく行われるのは,それらが独立であるという帰無仮説を立てて検定することである。本節ではその仕組みについて説明する。
カテゴリ変数のもつ統計的な情報は,カテゴリごとの度数だけである。そこで,2つのカテゴリ変数の間に関係について検討したいときには,まずそれらの組み合わせの度数を調べた表を作成する(Rではtable()やxtabs()という関数が使える)。これをクロス集計表と呼ぶ。とくに,2つのカテゴリ変数が,ともに2値変数のとき,そのクロス集計は2×2クロス集計表[2 by 2 cross tabulation](2×2分割表[2 by 2 contingency table])と呼ばれ,その統計的性質が良く調べられている。以下では2×2分割表の例で独立性のカイ二乗検定とフィッシャーの正確確率検定を説明するが,これらはカテゴリが3つ以上あっても通用する。同じ目的で使われる検定に,別名G検定とも呼ばれる尤度比検定があるが,これはRではvcdパッケージのassocstats()関数で計算できる。
なお,2つのカテゴリ変数の両方が順序のあるカテゴリである場合の独立性の検定としては,「線形連関の検定」(出典:藤井良宜『Rで学ぶデータサイエンス1 カテゴリカルデータ解析』共立出版, pp.65-68,英語ではAgresti A (2002) Categorical Data Analysis. Hoboken, New Jersey: John Wiley & Sons.で,“linear-by-linear association test”と呼ばれている。SPSSの日本語版では「線型と線型による連関検定」と意味の通じにくい訳語になっているので注意)を使う方法もある。これは,2つの順序のあるカテゴリ変数の各個体に対して順序を整数のスコアとして与え,スコア間で計算したピアソンの積率相関係数を2乗した値にサンプルサイズから1を引いた値を掛けた統計量が,近似的に自由度1のカイ二乗分布に従うことから検定を実行するものであり,Rではcoinパッケージのlbl_test()関数で計算できる。
独立性の検定としては,2つのカテゴリ変数の間に関連がないと仮定した場合に推定される期待度数を求めて,それに観測度数が適合するかを検定するカイ二乗検定が最も有名である69。
| A | A | |
|---|---|---|
| B | a人 | b人 |
| B | c人 | d人 |
2つのカテゴリ変数AとBが,それぞれ「あり」「なし」の2つのカテゴリ値しかとらないとき,これら2つのカテゴリ変数の組み合わせは「AもBもあり(A ∩ B)」「AなしBあり(Ā ∩ B)」「AありBなし(A ∩ B̄)」「AもBもなし(Ā ∩ B̄)」の4通りしかない。それぞれの度数を数えあげた結果が,上記の表として得られたときに,母集団の確率構造が,
| A | A | |
|---|---|---|
| B | π11 | π12 |
| B | π21 | π22 |
であるとわかっていれば,N = a + b + c + dとして,期待される度数は,
| A | A | |
|---|---|---|
| B | Nπ11 | Nπ12 |
| B | Nπ21 | Nπ22 |
であるから,
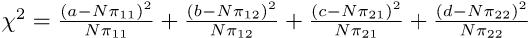 として,自由度3のカイ二乗検定をすればよいことになる。しかし,普通,πは未知である。そこで,Pr(Ā) = 1 − Pr(A)かつ,この2つのカテゴリ変数が独立ならばPr(A ∩ B) = Pr(A)Pr(B)と考えれば良い70ことを使って,Pr(A)とPr(B)を母数として推定する71。Pr(A)の点推定量は,Bを無視してAの割合と考えれば(a + c)/Nであることは自明である。同様に,Pr(B)の点推定量は,(a + b)/Nとなる。したがって,π11 = Pr(A ∩ B) = Pr(A)Pr(B) = (a + c)(a + b)/(N2)となる。
として,自由度3のカイ二乗検定をすればよいことになる。しかし,普通,πは未知である。そこで,Pr(Ā) = 1 − Pr(A)かつ,この2つのカテゴリ変数が独立ならばPr(A ∩ B) = Pr(A)Pr(B)と考えれば良い70ことを使って,Pr(A)とPr(B)を母数として推定する71。Pr(A)の点推定量は,Bを無視してAの割合と考えれば(a + c)/Nであることは自明である。同様に,Pr(B)の点推定量は,(a + b)/Nとなる。したがって,π11 = Pr(A ∩ B) = Pr(A)Pr(B) = (a + c)(a + b)/(N2)となる。
同様に考えれば,母集団の各セルの確率は下式で得られる。 π12 = (b + d)(a + b)/(N2) π21 = (a + c)(c + d)/(N2) π22 = (b + d)(c + d)/(N2)
これらの値を使えば,
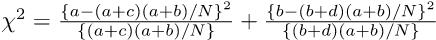
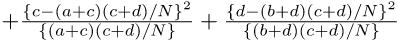
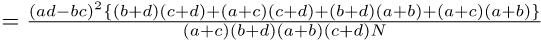 分子の中括弧の中はN2なので,結局,
分子の中括弧の中はN2なので,結局,
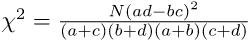
ただし通常は,イェーツの連続性の補正を行う。カイ二乗分布は連続分布なので,各度数に0.5を足したり引いたりしてやると,より近似が良くなるという発想である。この場合,
 が自由度1のカイ二乗分布に従うと考えて検定する。なお,|ad − bc|がN/2より小さいときは補正の意味がないので,χ2 = 0とするのが普通である。|ad − bc| < N/2のとき,Rの
が自由度1のカイ二乗分布に従うと考えて検定する。なお,|ad − bc|がN/2より小さいときは補正の意味がないので,χ2 = 0とするのが普通である。|ad − bc| < N/2のとき,Rのchisq.test()ではYatesの元論文の主旨に従うということで補正されてしまうけれども,prop.test()では補正されない。
実際の検定はクロス集計表が既に得られているとき,例えばa=12, b=8, c=9, d=10などとわかっていれば,Rコンソールでは,次のように入力すれば行列の定義とカイ二乗検定ができる。
x <- matrix(c(12,9,8,10), 2, 2)
# x <- matrix(c(12,8,9,10), 2, 2, byrow=TRUE) is also possible.
chisq.test(x)Rcmdrでは,「統計量」「分割表」「2元表の入力と分析」で表示される表の各セルに直接数字を入力し,必要な統計量のチェックボックスにチェックを入れてOKボタンをクリックするだけである。
例題
肺がんの患者100人に対して,1人ずつ性・年齢が同じ健康な人を対照として100人選び(この操作をペアマッチサンプリングという),それぞれについて過去の喫煙の有無を尋ねた結果,患者群では過去に喫煙を経験した人が80人,対照群では過去に喫煙を経験した人が55人だった。肺がんと喫煙は無関係といえるか? 独立性のカイ二乗検定をせよ。
帰無仮説は,肺がんと喫煙が無関係(独立)ということである。クロス集計表を作ってみると,
| 肺がん患者群 | 健康な対照群 | 合計 | |
|---|---|---|---|
| 過去の喫煙経験あり | 80 | 55 | 135 |
| 過去の喫煙経験なし | 20 | 45 | 65 |
| 合計 | 100 | 100 | 200 |
となる。肺がんと喫煙が無関係だという帰無仮説の下で期待される各カテゴリの人数は,
| 肺がんあり | 肺がん無し | |
|---|---|---|
| 喫煙あり | 135×100/200=67.5 | 135×100/200=67.5 |
| 喫煙なし | 65×100/200=32.5 | 65×100/200=32.5 |
となる。従って,連続性の補正を行なったカイ二乗統計量は,
χc2 = (80 − 68)2/67.5 + (55 − 67)2/67.5 + (20 − 32)2/32.5 + (45 − 33)2/32.5 = 13.128...となり,自由度1のカイ二乗分布で検定すると1-pchisq(13.128,1)より有意確率は0.00029...となり,有意水準5%で帰無仮説は棄却される。つまり,肺ガンの有無と過去の喫煙の有無には5%水準で統計学的に有意な関連があるといえる。
Rコンソールでは次の1行を打つだけで上の結果を得ることができる。
chisq.test(matrix(c(80, 20, 55, 45), 2, 2))Rcmdrでは,「統計量」「分割表」「2元表の入力と分析」で,対応するセルに直接人数を入力して[OK]をクリックすればよい。
例題
MASSパッケージのsurveyデータフレームで,性別(Sex)が利き手(W.Hnd)と独立であるという帰無仮説を検定せよ。
Rコンソールでは次の2行を打てばできる。
require(MASS)
chisq.test(xtabs(~ Sex+W.Hnd, data=survey))得られるp値は0.6274であり,性別と利き手の間に統計学的に有意な関連があるとはいえないことを意味する。
Rcmdrではsurveyデータフレームをアクティブにした後で,「統計量」「分割表」「2元表...」を選び,行の変数としてSexを,列の変数としてW.Hndを選び,[OK]をクリックする。アウトプットウィンドウに,X-squared = 0.5435, df = 1, p-value = 0.461と結果が表示される。これはYatesの補正なしの値である。Rcmdrでは,chisq.test()関数は必ずcorrect=FALSEオプション付きで実行される。
しかし,別の方法でYatesの補正ありの独立性のカイ二乗検定と同じ結果を得ることはできる。「統計量」の「比率」から「2標本の比率の検定」を選ぶ。既に書いた通り,グループとしてSex,目的変数としてW.Hndを指定し,検定のタイプとして「連続修正を用いた正規近似」にチェックを入れて[OK]ボタンをクリックすれば,p値として0.6274というYatesの補正をしたときの値が得られる。
期待度数が低い組み合わせがあるときには,カイ二乗検定での正規近似が非常に悪い近似になる。そういう場合,カテゴリを併合して変数を作り直し,組み合わせの種類を減らして,各組み合わせの頻度を上げる方法もあるが,恣意的なカテゴリの併合は結果を歪める可能性もあるし,元々カテゴリが2つずつだったらそれ以上減らせないので,もっといい方法が考案されている。それがフィッシャーの正確確率(検定)である。
ある2次元クロス集計表が与えられたとして,周辺度数を固定して(各々の変数については母比率が決まっていると仮定して)すべての組み合わせを考え,それらが起こる確率(超幾何分布に従う)を1つずつ計算し,得られている集計表が得られる確率よりも低い確率になるような表が得られる確率をすべて足し合わせてしまえば,2つのカテゴリ変数の間に関連がないという帰無仮説の下でそういう表が偶然得られる確率がどれほど低いのかを,直接計算することができる。こうして計算される確率を,フィッシャーの正確確率という。これなら,近似ではないので,期待度数が低い組み合わせがあっても問題ない。
もう少し丁寧に言うと,サイズNの有限母集団があって,そのうち変数Aの値が1である個体数がm1,1でない個体数がm2あるときに,変数Bの値が1である個体数がn1個(1でない個体数がn2 = N − n1個)あるという状況を考え,このn1個のうち変数Aの値が1である個体数がちょうどaである確率を求めることになる。これは,m1個からa個を取り出す組み合わせの数とm2個からn1 − a個を取り出す組み合わせの数を掛けて,N個からn1個を取り出す組み合わせの数で割った値になる。これと同じ周辺度数をもつ2×2分割表のうち,確率がこれと同じかこれよりも小さい表の確率をすべて足し合わせたものが,「変数Aと変数Bが独立」という帰無仮説が成り立つ確率になる。
有限母集団からの非復元抽出になるので,平均E(a)と分散V(a)は, E(a) = n1m1/N V(a) = {(N − n1)/(N − 1)}n1(m1/N)(m2/N) = (m1m2n1n2)/{N2(N − 1)} となる。実際には組み合わせ計算が多いので,手計算で実行することはまずありえず,統計ソフトにやらせることになる。また,個々の2×2分割表の確率は離散値をとるので,同じ確率の表がありうる場合に,それを足し算に含めるのかどうかは難しい点である。
しかし,フィッシャーの正確確率は,近似を使わないので,クロス集計表を使って2つのカテゴリ変数間の独立性の検定をするときは,コンピュータが使えるならば,サンプルサイズがよほど大きくない限り,常にカイ二乗検定ではなく,フィッシャーの正確な確率を求めるべきである。Rコンソールで実行するのは簡単で,カイ二乗検定でchisq.test()と書かれていたところを,fisher.test()で置き換えればいい。
例題
MASSパッケージのsurveyデータフレームについて,性別(Sex)と喫煙習慣(Smoke)が独立であるとしたときに,実際得られている組み合わせあるいはそれより起こりにくい組み合わせが偶然得られる確率を,フィッシャーの正確確率によって計算せよ。
Rコンソールでは次の2行を打てばよい。
require(MASS)
fisher.test(xtabs(~Sex+Smoke, data=survey))
Rcmdrでは,surveyデータフレームをアクティブにしておき,「統計量」「分割表」「2元表の分析」として行の変数としてSex,列の変数としてSmokeを選んでから,「フィッシャーの正確検定」にチェックを入れて[OK]ボタンをクリックする。
どちらもp-value = 0.3105という同じ結果を示す。したがって,性別と喫煙習慣が無関係である可能性は有意水準5%で否定できない。
ここまで説明した検定は,2つのカテゴリ変数が独立であるという帰無仮説の検定であって,得られるp値が有意水準より小さくて帰無仮説が棄却された場合,p値の小ささは関連がない可能性がどれほど低いかを示す意味しか無く,どの程度の関連があるかは示さない。ただし,フィッシャーの正確確率を得る関数の出力をよく見ると,オッズ比が表示されており,このオッズ比は関連の大きさを示す指標の一つである。
「独立でない」場合について,関連の強さを評価したいときに用いる指標について述べよう。「相関と回帰」の章に示すように,量的な変数(連続変数)の場合は相関係数が関連の強さの指標となるが,カテゴリ変数の場合は,既に述べたオッズ比やリスク比のほか,ファイ係数(記号はφを用いるのが普通)と呼ばれる指標は,要因の有無,発症の有無を1,0で表した場合のピアソンの積率相関係数と同じ計算式で得られる。正の関連性だけ考えるなら,π1,π2を要因ありの発症者割合,要因なしの発症者割合,θ1,θ2を発症者中の要因あり割合,非発症者中の要因あり割合として,φ = √(π1 - π1)(θ1 - θ1)である。実は二乗してNを掛けると連続修整無しのカイ二乗値に一致する。以下のコードを試されたい。
phi <- function(X) { # Xは2×2の行列
M <- rowSums(X)
N <- colSums(X)
phi0 <- (X[1,1]/M[1]-X[2,1]/M[2])*(X[1,1]/N[1]-X[1,2]/N[2])
phi1 <- ifelse(phi0<0, -sqrt(-phi0), sqrt(phi0))
phi2 <- (X[1,1]*X[2,2] - X[1,2]*X[2,1])/sqrt(M[1]*M[2]*N[1]*N[2])
return(c(phi1, phi2))}
XX <- matrix(c(80, 20, 55, 45), 2, 2)
phi(XX)
phi(XX)^2*sum(XX)
chisq.test(XX, correct=FALSE)$statistic同様の目的でピアソンのコンティンジェンシー係数やCramerのVという係数も用いられる。以上すべてはvcdパッケージのassocstats()関数にクロス集計表を与えると計算してくれる。
また,カテゴリ変数または順序変数間の相関関係をみるには,ポリコリック相関係数を用いる方法もある(関連して書いておくと,順序変数と量的変数の間の関連は,ポリシリアル相関係数でみることができる)。これらは,polycorパッケージに含まれており,前者はpolychor()関数(2つのカテゴリ変数を与える。標準誤差が欲しいときはstd.err=TRUEオプションを付ける),後者はpolyserial()関数で求めることができる。
ポリコリック相関係数の計算例
> library(MASS) # surveyデータフレームを含む
> library(polycor) # 未インストールの際は一度だけ以下を実行
> # install.packages("polycor", dep=TRUE)
要求されたパッケージ mvtnorm をロード中です
要求されたパッケージ sfsmisc をロード中です
> polychor(survey$Smoke, survey$Exer, std.err=TRUE)
Polychoric Correlation, 2-step est. = -0.042 (0.1006)
Test of bivariate normality: Chisquare = 5.628, df = 5, p = 0.3441
> # カテゴリ順序を付け直す。
> # EZRでは「アクティブデータセット」「変数の操作」「因子水準を再順序化する」
> survey$Smoke <- factor(survey$Smoke,
levels=c("Never", "Occas", "Regul", "Heavy"), ordered=TRUE)
> survey$Exer <- factor(survey$Exer,
levels=c("None","Some","Freq"), ordered=TRUE)
> xtabs(~Smoke+Exer, data=survey)
Exer
Smoke None Some Freq
Never 18 84 87
Occas 3 4 12
Regul 1 7 9
Heavy 1 3 7
> polychor(survey$Smoke, survey$Exer, std.err=TRUE)
Polychoric Correlation, 2-step est. = 0.1269 (0.1011)
Test of bivariate normality: Chisquare = 4.274, df = 5, p = 0.5107正しい順序の順序変数にすると,ポリコリック相関係数は,順序を無視したときとは結果が変わることがわかる(もちろん,後述するようにカイ二乗検定やフィッシャーの正確検定の結果は,順序の情報を使わないので変わらない)。順序変数の間では,量的変数としての扱いを強制し,スピアマンの順位相関係数を求めることもできるが,同順位が多いためp値が正しく得られないという問題を生じるので,ポリコリック相関係数を使う方が良い。
3群以上を比較するために,単純に2群間の差の検定を繰り返すことは誤りである。なぜなら,n群から2群を抽出するやりかたはnC2通りあって,1回あたりの第1種の過誤(本当は差がないのに,誤って差があると判定してしまう確率)を5%未満にしたとしても,3群以上の比較全体として「少なくとも1組の差のある群がある」というと,全体としての第1種の過誤が5%よりずっと大きくなってしまうからである。
この問題を解消するには,多群間の比較という捉え方をやめて,群分け変数が注目している量の変数に与える効果があるかどうかという捉え方にするのが一つの方法であり,具体的には一元配置分散分析やクラスカル=ウォリス(Kruskal-Wallis)の検定がこれに当たる。
そうでなければ,有意水準5%の2群間の検定を繰り返すことによって全体として第1種の過誤が大きくなってしまうことが問題なので,第1種の過誤を調整することによって全体としての検定の有意水準を5%に抑える方法もある。このやり方は「多重比較法」と呼ばれる。
一元配置分散分析では,データのばらつき(変動)を,群間の違いという意味のはっきりしているばらつき(群間変動)と,各データが群ごとの平均からどれくらいばらついているか(誤差)をすべての群について合計したもの(誤差変動)に分解して,前者が後者よりもどれくらい大きいかを検討することによって,群分け変数がデータの変数に与える効果があるかどうかを調べる。
例えば,南太平洋の3つの村X, Y, Zで健診をやって,成人男性の身長や体重を測ったとしよう。このとき,データは例えば次のようになる(架空のものである)。このデータはhttps://minato.sip21c.org/grad/sample2.datとして公開してあり,Rからread.delim()関数で読み込める。
| ID番号 | 村落(VG) |
身長(cm)(HEIGHT) |
|---|---|---|
| 1 | X | 161.5 |
| 2 | X | 167.0 |
| (中略) | ||
| 22 | Z | 166.0 |
| (中略) | ||
| 37 | Y | 155.5 |
村落によって身長に差があるかどうかを検定したいならば,HEIGHTという量的変数に対して,VGという群分け変数の効果があるかどうかを一元配置分散分析することになる。Rコンソールでは以下のように入力する。
> sp <- read.delim("https://minato.sip21c.org/grad/sample2.dat")
> summary(aov(HEIGHT ~ VG, data=sp))すると,次の枠内に示す「分散分析表」が得られる。
Df Sum Sq Mean Sq F value Pr(>F)
VG 2 422.72 211.36 5.7777 0.006918 **
Residuals 34 1243.80 36.58
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1 右端の*の数は有意性を示す目安だが,確率そのものに注目してみるほうがよい。Sum Sqのカラムは偏差平方和を意味する。VGのSum Sqの値422.72は,村ごとの平均値から総平均を引いて二乗した値を村ごとの人数で重み付けした和であり,群間変動または級間変動と呼ばれ,VG間でのばらつきの程度を意味する。ResidualsのSum Sqの値1243.80は各個人の身長からその個人が属する村の平均身長を引いて二乗したものの総和であり,誤差変動と呼ばれ,村によらない(それ以外の要因がないとすれば偶然の)ばらつきの程度を意味する。Mean Sqは平均平方和と呼ばれ,偏差平方和を自由度(Df)で割ったものである。平均平方和は分散なので,VGのMean Sqの値211.36は群間分散または級間分散と呼ばれることがあり,ResidualsのMean Sqの値36.58は誤差分散と呼ばれることがある。F valueは分散比と呼ばれ,群間分散の誤差分散に対する比である。この場合の分散比は第1自由度2,第2自由度34のF分布に従うことがわかっているので,それを使った検定の結果,分散比がこの実現値よりも偶然大きくなる確率(Pr(>F)に得られる)が得られる。この例では0.006918なので,VGの効果は5%水準で有意であり,帰無仮説は棄却される。つまり,身長は村落によって有意に異なることになる。
EZRでsample2.datをspというデータフレームに読み込むには,[ファイル]の[データのインポート]から[テキストファイル,クリップボードまたはURLから]と進んで,[データフレーム名を入力:]のところにspと打ち,[インターネットURL]の右側のラジオボタンをチェックし,フィールド区切りを[タブ]として[OK]をクリックして表示されるダイアログにhttps://minato.sip21c.org/grad/sample2.datと入力して[OK]する。
ANOVAを実行するには,[統計解析]の[連続変数の解析]で[三群以上の間の平均値の比較(一元配置分散分析one-way ANOVA)]を選び,「目的変数」としてHEIGHTを,「比較する群」としてVGを選び,[OK]をクリックすればよい。エラーバー付きの棒グラフが自動的に描かれ,アウトプットウィンドウには分散分析表に続いて,村ごとの平均値と標準偏差の一覧表が表示される。右端のp値は一元配置分散分析におけるVGの効果の検定結果を再掲したものになっている。
古典的な統計解析では,各群の母分散が等しいことを確認しないと一元配置分散分析の前提となる仮定が満たされない。母分散が等しいという帰無仮説を検定するには,バートレット(Bartlett)の検定と呼ばれる方法がある。Rでは,量的変数をY,群分け変数をCとすると,bartlett.test(Y~C)で実行できる(もちろん,これらがデータフレームdatに含まれる変数ならば,bartlett.test(Y~C, data=dat)とする)。この結果得られるp値は0.5785なので,母分散が等しいという帰無仮説は有意水準5%で棄却されない。これを確認できると,安心して一元配置分散分析が実行できる。
EZRでは,メニューバーの「統計解析」から「連続変数の解析」の「三群以上の等分散性の検定(Bartlett検定)」を選び,「目的変数」としてHEIGHT,「グループ」としてVGを選んで[OK]する。
しかし,このような2段階の検定は,検定の多重性の問題を起こす可能性がある。群馬大学の青木繁伸教授や三重大学の奥村晴彦教授の数値実験によると,等分散であるかどうかにかかわらず,2群の平均値の差のWelchの方法を多群に拡張した方法を用いるのが最適である。Rではoneway.test()で実行できる。上記,村落の身長への効果をみる例では,oneway.test(HEIGHT ~ VG, data=sp)と打てば,Welchの拡張による一元配置分散分析ができて,以下の結果が得られる。
> oneway.test(HEIGHT ~ VG, data=sp)
One-way analysis of means (not assuming equal variances)
data: HEIGHT and VG
F = 7.5163, num df = 2.00, denom df = 18.77, p-value = 0.004002Rcmdrではメニューにないので,スクリプトウィンドウでaovの部分をoneway.testに書き直して「実行」するしかなかったが,EZRは1.21から一元配置分散分析のメニューウィンドウに「Welch検定」として等分散を仮定しないオプションが追加された。
ケンブリッジ大学の統計Wikiの効果量についてのFAQ72によると,一元配置分散分析の効果量は,通常η2という記号(イータ二乗とかイータスクウェアドと読む)で示される「効果の偏差平方和を,それ自身とその効果に関連した誤差の偏差平方和の和で割った値」になる。これは,分散分析表で得られる分散比であるF,グループ数k,サンプルサイズをNとすると,η2 = F×(k-1) / {F×(k-1) + (N-k)}で得られ73,目安として0.01以上0.06未満で弱い効果,0.06以上0.14未満で中程度の効果,0.14以上で大きな効果であるとされている。
RcmdrやEZRのメニューには含まれていないが,Rでは,lsrパッケージのetaSquared()関数や,rstatixパッケージのeta_squared()関数に,aov()関数の出力オブジェクトを与えれば計算できる。これらの関数には,等分散を仮定しないoneway.test()関数の出力オブジェクトは与えることができないが,F値とグループ数とサンプルサイズを使った式が等分散を仮定しない場合にも成り立つとすれば,上の式から計算できる。
6種類の異なる餌をヒヨコに与えて育てた後の鶏の体重データであるchickwtsを使った実行例を以下に示しておく。どの計算方法でも,等分散を仮定したANOVAについてはη2 = 0.542となることがわかる。等分散を仮定しないWelchのANOVAについてはη2 = 0.602となる(正しいかどうかは確認が十分に取れていないので注意)。いずれにせよ,与える餌の種類が鶏の体重に与える効果は大きいと言える。
# 普通のANOVA
res <- aov(weight ~ feed, data=chickwts)
summary(res)
# 偏差平方和から計算
SS <- summary(res)[[1]]$"Sum Sq"
SS[1] / (SS[1]+SS[2]) # eta squared
# F値とグループ数とサンプルサイズから計算
.k <- length(levels(chickwts$feed))
.N <- length(chickwts$feed)
.F <- summary(res)[[1]]$"F value"[1]
.F * (.k-1) / (.F * (.k-1) + .N - .k) # eta squared
# lsrパッケージ
library(lsr)
etaSquared(res, anova=TRUE)
# rstatixパッケージ
library(rstatix)
eta_squared(res)
# 等分散を仮定しないWelchのANOVA
res2 <- oneway.test(weight ~ feed, data=chickwts)
res2
..F <- res2$statistic
..F * (.k-1) / (..F * (.k-1) + .N - .k) # eta squared?多群間の差を調べるためのノンパラメトリックな方法としては,クラスカル=ウォリス(Kruskal-Wallis)の検定が有名である。Rでは,量的変数をY,群分け変数をCとすると,kruskal.test(Y~C)で実行できる。以下,Kruskal-Wallisの検定の仕組みを箇条書きで説明する。
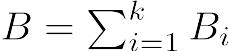 としてBを求め,H = 12 ⋅ B/{N(N + 1)}としてHを求める。同順位を含むときは,すべての同順位の値について,その個数に個数の2乗から1を引いた値を掛けたものを計算し,その総和をAとして,
としてBを求め,H = 12 ⋅ B/{N(N + 1)}としてHを求める。同順位を含むときは,すべての同順位の値について,その個数に個数の2乗から1を引いた値を掛けたものを計算し,その総和をAとして,
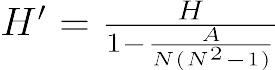 によりHを補正した値H′を求める。
によりHを補正した値H′を求める。上の例で村落の身長への効果をみるには,Rコンソールでは,
kruskal.test(HEIGHT ~ VG, data=sp)と打てば結果が表示される。
Rcmdrでは,「統計量」,「ノンパラメトリック検定」,「クラスカル-ウォリスの検定...」と選び,「グループ」としてVGを,「目的変数」としてHEIGHTを選び,[OK]をクリックする。
EZRでは,「統計解析>ノンパラメトリック検定>3群以上の間の比較(Kruskal-Wallis検定)」と選び,目的変数(1つ選択)の枠でHEIGHTを,グループ(1つ選択)の枠でVGを選び,[OK]をクリックする。
Fligner-Killeenの検定は,グループごとのばらつきに差が無いという帰無仮説を検定するためのノンパラメトリックな方法である。Bartlettの検定のノンパラメトリック版といえる。上の例で,身長のばらつきに村落による差が無いという帰無仮説を検定するには,Rコンソールでは,fligner.test(HEIGHT ~ VG, data=sp)とすればよい。
EZRやRcmdrのメニューには入っていないので,必要な場合はスクリプトウィンドウにコマンドを打ち,選択した上で「実行」ボタンをクリックする。
RcmdrやEZRには含まれていないが,https://rcompanion.org/rcompanion/で"An R Companion for the Handbook of Biological Statistics"という素晴らしいテキスト(デラウェア大学のJohn H. McDonaldによるテキスト"Handbook of Biological Statistics"74の例を使ってRによる解析方法を示すために,ラトガース大学のSalvatore S. Mangiafico准教授が書いたもの)が公開されており,そのために作られたrcompanionパッケージを使うと,epsilonSquared()関数やordinalEtaSquared()関数で効果量が推定できる。
epsilonSquared()関数で得られるϵ2は,目安として0.01以上0.08未満で弱い効果,0.08以上0.26未満で中程度の効果,0.26以上で大きな効果とされている。ordinalEtaSquared()関数で得られるのはη2なので,効果の大きさの目安はANOVAの場合と同様である。
ANOVAの場合と同じく,chickwtsデータを使った実行例を示しておく。ϵ2 = 0.533,η2 = 0.498となるので,与える餌の種類は鶏の体重に大きな効果をもっていると言える。なお,epsilonSquared()関数にci=TRUEオプションを付けることにより,ブートストラップ法で求めたη2の95%信頼区間が得られる。
kruskal.test(weight ~ feed, data=chickwts)
library(rcompanion)
epsilonSquared(chickwts$weight, chickwts$feed, ci=TRUE)
ordinalEtaSquared(chickwts$weight, chickwts$feed)多重比較の方法にはいろいろあるが,良く使われているものとして,ボンフェローニ(Bonferroni)の方法,ホルム(Holm)の方法,シェフェ(Scheffé)の方法,テューキー(Tukey)のHSD,ダネット(Dunnett)の方法,ウィリアムズ(Williams)の方法がある。最近は,FDR(False Discovery Rate)法もかなり使われるようになった。ボンフェローニの方法とシェフェの方法は検出力が悪いので,特別な場合を除いては使わない方が良い。テューキーのHSDまたはホルムの方法が薦められる。なお,ダネットの方法は対照群が存在する場合に対照群と他の群との比較に使われるので,適用場面が限定されている75。ウィリアムズの方法は対照群があって他の群にも一定の傾向が仮定される場合には最高の検出力を発揮するが,ダネットの方法よりもさらに限られた場合にしか使えない。
テューキーのHSDは平均値の差の比較にしか使えないが,ボンフェロー二の方法,ホルムの方法,FDR法は位置母数のノンパラメトリックな比較にも,割合の差の検定にも使える。Rコンソールでは,pairwise.t.test(),pairwise.wilcox.test(),pairwise.prop.test()という関数で,ボンフェローニの方法,ホルムの方法,FDR法による検定の多重性の調整ができる。fmsbパッケージを使えば,pairwise.fisher.test()により,Fisherの直接確率法で対比較をした場合の検定の多重性の調整も可能である。
なお,Bonferroniのような多重比較法でp値を調整して表示するのは表示上の都合であって,本当は帰無仮説族レベルでの有意水準を変えているのだし,p.adjust.method="fdr"でも,p値も有意水準も調整せず,帰無仮説の下で偶然p値が有意水準未満になって棄却されてしまう確率(誤検出率)を計算し,帰無仮説ごとに有意水準に誤検出率を掛けてp値との大小を比較して検定するということになっているが,これは弱い意味で帰無仮説族レベルでの有意水準の調整を意味する,と原論文に書かれているので,統計ソフトがp値を調整した値を出してくるのはやはり表示上の都合で,本当は有意水準を調整している(参照:Benjamini Y, Hochberg Y: Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. Royal Stat. Soc. B, 57: 289-300, 1995.)。
Bonferroni,Holm,FDRという3つの多重比較の考え方はシンプルでわかりやすいので,ここで簡単にまとめておく。k個の帰無仮説について検定して得られたp値がp(1) < p(2) < ... < p(k)だとすると,有意水準αで帰無仮説族の検定をするために,Bonferroniはp(1)から順番にα/kと比較し,p(i) ≥ α/kになったところ以降判定保留,Holmはp(i) ≥ α/(k − i + 1)となったところ以降判定保留とする。有意水準αでFDR法をするには,まずp(k)をαと比較し,次にp(k − 1)をα(k − 1)/kと比較し,とp値が大きい方から比較していき,p(i) < α × i/kとなったところ以降,i個の帰無仮説を棄却する。Rのpairwise.*.test()では,Bonferroniならすべてのp値がk倍されて表示,Holmでは小さい方からi番目のp値が(k − i + 1)倍されて表示,fdrでは小さい方からi番目のp値がk/i倍されて表示されることによって,表示されたp値を共通のαとの大小で有意性判定ができるわけだが,これは表示上の都合である。(残念ながら,FDR法はまだRcmdrやEZRのメニューには含まれていない)
実例を示そう。先に示した3村落の身長データについて,どの村落とどの村落の間で身長に差があるのかを調べたい場合,Rコンソールでは,
pairwise.t.test(sp$HEIGHT, sp$VG, p.adjust.method="bonferroni")
とすれば,2村落ずつのすべての組み合わせについてボンフェローニの方法で有意水準を調整したp値が表示される("bonferroni"は"bon"でも良い。また,pairwise.*系の関数ではdata=というオプションが使えないので,データフレーム内の変数を使いたい場合は,予めデータフレームをattach()しておくか,またはここで示したように,変数指定の際に一々,“データフレーム名$”を付ける必要がある)。
pairwise.wilcox.test(sp$HEIGHT, sp$VG, p.adjust.method="bonferroni")とすれば,ボンフェローニの方法で有意水準を調整した,すべての村落間での身長の差を順位和検定した結果を出してくれる。これらの関数で,p.adjust.methodを指定しなければホルムの方法になるが,明示したければ,p.adjust.method="holm"とすればよい。FDR法を使うには,p.adjust.method="fdr"とすればよい。Rでもボンフェローニが可能なのは,一番単純な方法であるという理由と,ホルムの方法に必要な計算がボンフェローニの計算を含むからだと思われる。なお,Rを使って分析するのだけれども,データがきれいな正規分布をしていて,かつ古典的な方法の論文しかacceptしない雑誌に対してどうしても投稿したい,という場合は,TukeyHSD(aov(HEIGHT ~ VG, data=sp))などとして,テューキーのHSDを行うことも可能である。
Rcmdrの場合は,「統計量」の「平均」から「1元配置分散分析」を選んで実行するときに,「2組ずつの平均の比較(多重比較)」の左のボックスにチェックを入れておけば,自動的にTukeyのHSDで検定の多重性を調整した対比較を実行してくれるし,同時信頼区間のグラフも表示される。しかし,第一種の過誤を調整する方法は,まだサポートされていない。
EZRでは,一元配置分散分析メニューのオプションとして実行できる。「統計解析」「連続変数の解析」「3群以上の平均値の比較(一元配置分散分析one-way ANOVA)」を選んで,「目的変数」としてHEIGHTを,「比較する群」としてVGを選んでから,下の方の「↓2組ずつの比較(post-hoc検定)は比較する群が1つの場合のみ実施される」から欲しい多重比較法の左側のボックスにチェックを入れてから「OK」ボタンをクリックする。ただし,等分散を仮定しない「一般化Welch検定」の場合は,多重比較オプションが使えない。
これは,RmcdrやEZRに実装されている,BonferroniやHolmの方法で多重性を調整したt検定やTukeyの方法が等分散を仮定しているためである。
いずれのやり方をしても,2群ずつの対比較の結果が得られる。例えばTukeyHSDの場合だと,2群ずつの対比較の結果として,差の推定値と95%同時信頼区間に加え,Tukeyの方法で検定の多重性を調整したp値が下記のように表示され,検定の有意水準が5%だったとすると,ZとYの差だけが有意であることがわかる。
> TukeyHSD(AnovaModel.3, "factor(VG)")
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = HEIGHT ~ factor(VG), data = sp, na.action = na.omit)
$`factor(VG)`
diff lwr upr p adj
Y-X -2.538889 -8.3843982 3.30662 0.5423397
Z-X 5.850000 -0.9598123 12.65981 0.1038094
Z-Y 8.388889 2.3382119 14.43957 0.0048525実は,等分散を仮定しない多重比較も存在する。Games-Howell法(元論文:Games PA, Howell JF (1976) Pairwise Multiple Comparison Procedures with Unequal N’s Pairwise Multiple Comparison Procedures with Unequal N’s and/or Variances: A Monte Carlo Study. Journal of Educational Statistics, 1(2) : 113-125.)と呼ばれる。
群馬大学青木先生のwebサイトのTukey法のページ76に説明とRコードが掲載されている。そのため,青木先生のコードを利用している弘前大学の「改変Rコマンダー」77ではGames-Howell法が実行可能である。青木先生のコードについては,英語だが,http://www.gcf.dkf.unibe.ch/BCB/files/BCB_10Jan12_Alexander.pdfの説明もわかりやすい。他にオリジナルなコードとして,https://gist.github.com/aschleg/ea7942efc6108aedfa9ec98aeb6c2096も存在するが,おそらくrosettaパッケージのposthocTGH()関数を使うのが簡単だろう(注:この関数は,以前はuserfriendlyscienceパッケージに入っていたが,ufsという名前に変わったときに,posthocTGH()関数はrosettaパッケージに移ったようだ。弘前大学のサイトの説明を見た限りでは,R-4.0.5以降の変更らしい)。Rの組み込みデータであるchickwts(6種類の餌[feed]で育てた鶏の体重[weight]の比較)を使って実行する例を示しておく。ちなみに,このコードでgames-howellとなっているところをtukeyにすれば,TukeyHSD()関数を使った場合と同じ結果が得られる。
if (require(rosetta)==FALSE) {
install.packages("rosetta", dep=TRUE)
library(rosetta) }
posthocTGH(chickwts$weight, chickwts$feed, method="games-howell")Dunnettの多重比較は,コントロールと複数の実験群の比較というデザインで用いられる。以下,簡単な例で示す。例えば,5人ずつ3群にランダムに分けた高血圧患者がいて,他の条件(食事療法,運動療法など)には差をつけずに,プラセボを1ヶ月服用した群の収縮期血圧(mmHg単位)の低下が5, 8, 3, 10, 15で,代表的な薬を1ヶ月服用した群の低下は20, 12, 30, 16, 24で,新薬を1ヶ月服用した群の低下が31, 25, 17, 40, 23だったとしよう。このとき,プラセボ群を対照として,代表的な薬での治療及び新薬での治療に有意な血圧降下作用の差が出るかどうかを見たい(悪くなるかもしれないので両側検定で)という場合に,Dunnettの多重比較を使う。Rでこのデータをbpdownというデータフレームに入力して Dunnettの多重比較をするためには,次のコードを実行する。
> bpdown <- data.frame(
+ medicine=factor(c(rep(1,5),rep(2,5),rep(3,5)),
+ labels=c("プラセボ","代表薬","新薬")),
+ sbpchange=c(5, 8, 3, 10, 15, 20, 12, 30, 16, 24, 31, 25, 17, 40, 23))
> summary(res1 <- aov(sbpchange ~ medicine, data=bpdown))
> library(multcomp)
> res2 <- glht(res1, linfct = mcp(medicine = "Dunnett"))
> confint(res2, level=0.95)
> summary(res2)つまり,基本的には,multcompパッケージを読み込んでから,分散分析の結果をglht()関数に渡し,linfctオプションで,Dunnettの多重比較をするという指定を与えるだけである。multcompパッケージのバージョン0.993まで使えたsimtest()関数は,0.994から使えなくなったので注意されたい。
EZRでは,まず「ファイル」「データのインポート」「ファイルまたはクリップボード,URLからテキストデータを読み込む」として,「データセット名を入力」の右側のボックスにbpdownと入力し,「データファイルの場所」として「インターネットのURL」の右側のラジオボタンをクリックし,「フィールドの区切り記号」を「タブ」にして「OK」ボタンをクリックする。表示されるURL入力ウィンドウにhttps://minato.sip21c.org/bpdown.txtと打って「OK」ボタンをクリックすれば,上記データを読み込むことができる。
そこで「統計解析」の「連続変数の解析」から「3群以上の平均値の比較(一元配置分散分析one-way ANOVA)」を選んで,「目的変数」としてsbpchange,「比較する群」としてmedicineを選び,「2組ずつの比較(Dunnettの多重比較)」の左のチェックボックスをチェックしてから「OK」ボタンをクリックすればいい。
なお,このデータで処理名を示す変数medicineの値としてo.placebo,1.usual,2.newdrugのように先頭に数字付けた理由は,それがないと水準がアルファベット順になってしまい,Dunnettの解析において新薬群がコントロールとして扱われてしまうからである。
ノンパラメトリック検定の場合は,「統計解析」の「ノンパラメトリック検定」から「3群以上の間の比較(Kruskal-Wallis検定)」と選び,「目的変数」をsbpchange,「グループ」をmedicineにし,「2組ずつの比較(post-hoc検定、Steelの多重比較)」の左のチェックボックスをチェックして「OK」ボタンをクリックすれば,Steelの多重比較が実行できる。
prop.test()関数は,3群以上の間でも,「どの群でも事象の生起確率に差がない」という帰無仮説を検定するのに使える。例えば,A, B, Cという3つの処理を実施したときの脱落が,A: 0/15, B: 2/13, C: 1/14であったとき,「3つの処理間で脱落率に差が無い」という帰無仮説の下で期待される脱落率は, (0+2+1) / (15+13+14) = 3/42
これが正しければ,期待されるクロス表は
| A | B | C | |
|---|---|---|---|
| 脱落 | 15×(3/42) | 13×(3/42) | 14×(3/42) |
| 完了 | 15×(39/42) | 13×(39/42) | 14×(39/42) |
すべてのセルについて,観測度数と期待度数の差の2乗を期待度数で割った値を合計したものがカイ二乗値χ2
χ2 = (0 − 15 × (3/42))2/(15 × (3/42)) + ... = 2.485...
χ2は自由度2(3処置,2種類の結果だから,それぞれから1を引いて積をとったものが自由度)のカイ二乗分布に従う。 1-pchisq(X2, 2)を計算すると(注:pchisq(X2, 2)は自由度2のカイ二乗分布のX2までの確率密度の積分値),0.2886となる。Rコンソールでは,
prop.test(c(0, 2, 1), c(15, 13, 14), correct=FALSE)と打てば,X-squared = 2.4852, df = 2, p-value = 0.2886と結果が得られる。
この例では脱落数が少ないので,カイ二乗検定では近似が悪い。そういう場合は,「処理間で脱落率に差が無い」という帰無仮説は,「脱落するかどうかは処理の種類と無関係(=独立)」という帰無仮説と同値なので,以下のクロス表を想定し,フィッシャーの正確な検定(Fisher’s exact test)を実行する。
| A | B | C | 合計 | |
|---|---|---|---|---|
| 脱落 | 0 | 2 | 1 | 3 |
| 完了 | 15 | 11 | 13 | 39 |
| 合計 | 15 | 13 | 14 | 42 |
「脱落するかどうか」と「処理の種類」が偶然この組合せになっている確率を計算するには,この表と同じ周辺度数をもつクロス表(例えば下記)をすべて考え,それぞれが偶然得られる確率を計算する。下表の確率は,15C1×13C1×14C1/42C3で,約0.238となる。実際の脱落データの表は,15C0×13C2×14C1/42C3で,約0.095となる。
| A | B | C | 合計 | |
|---|---|---|---|---|
| 脱落 | 1 | 1 | 1 | 3 |
| 完了 | 14 | 12 | 13 | 39 |
| 合計 | 15 | 13 | 14 | 42 |
実際の表より偶然得られる確率が小さな表の確率を合計すると,フィッシャーの正確な確率が得られる。つまり,0.095 + 0.040 + 0.025 + 0.032 = 0.192となる。Rコンソールでは,fisher.test(matrix(c(0, 15, 2, 11, 1, 13), 2, 3)で0.1914となる(違いは丸め誤差)である。
2群ずつ比べて,どの群間で差があるのかをみようとすると,平均値の場合と同様に検定の多重性が生じるので,平均値の差の場合と同様,第一種の過誤を調整する必要があり,ボンフェローニの方法やホルムの方法,あるいはFDR法を用いることになる。Rの関数はpairwise.prop.test()である。
なお,3群以上の間で事象の生起確率に一定の傾向がみられるかどうかを調べたい場合には,コクラン=アーミテージの検定という手法がある。例えば,漁師100人,農民80人,事務職30人について便の検査をして,日本住血吸虫虫卵陽性者が60人,30人,8人だったとしたとき,職業的な貝との接触リスクに対して勝手に漁師を4,農民を2,事務職を1とスコアリングして,陽性割合の増加傾向が,このスコアと同じかどうかを調べることができる。この場合なら,Rコンソールのコマンドは以下のようになる。
total <- c(100, 80, 30)
epos <- c(60, 30, 8)
prop.test(epos, total)
pairwise.prop.test(epos, total)
orisk <- c(4, 2, 1)
prop.trend.test(epos, total, orisk)Rcmdrでは「統計量」「比率」メニューには1標本と2標本の場合しかないので指定できない。しかし,実は3群以上で「どの群でも事象の生起確率に差がない」という帰無仮説を検定することは,後述するクロス集計表の考え方をすれば,「群分け変数と事象の有無を示す変数が独立」という帰無仮説の検定と同じことなので,「統計量」の「分割表」の「2元表」で行の変数,列の変数として,群分け変数と事象の有無を示す変数をそれぞれ指定すれば可能である。集計済みのデータの場合も,「統計量」「分割表」「2元表の入力と分析」を選び,この例なら行数を2のまま,列数を3にし,表に数値を入力して,[OK]ボタンをクリックすれば,検定ができる(ただし,prop.test()と異なり,Yatesの連続性の修正を行うオプションは提供されていない点には注意が必要である)。なお,pairwise.prop.test()やprop.trend.test()は,Rcmdrではサポートされていない。
EZRでは,「統計解析」「名義変数の解析」から「分割表の直接入力と解析」を選び,列数バーを一つ右にずらして2行3列の分割表にしてから数値を入力する。行ラベルと列ラベルの欄には整数が入っているが文字列に書き換えることができる。日本語も入力可能である。「仮説検定」のところで独立性のカイ2乗検定(連続補正有り)の左のボックスにチェックを入れれば,Yatesの連続性の補正をした検定結果が得られる。コクラン=アーミテージ検定は,生データから計算するメニューはあるが,集計後データからは計算できないので,実行したい場合はそのような生データを生成する必要がある(詳細は省略)。
生データから計算する場合について,MASSパッケージのsurveyデータセットを使って例示しよう。Clapという変数は,両手を叩き合わせたときにどちらが上に来るかを意味し,左,右,どちらでもない,という3つのカテゴリからなる。W.Hndは字を書く手がどちらか,つまり利き手を意味する。両手を叩き合わせたときに上に来る手の3タイプ間で,左利きの割合に差が無いという帰無仮説を検定する。次いで,3タイプ中のすべての2タイプの組み合わせについて,左利きの割合に差が無いという帰無仮説を検定し,第一種の過誤をホルムの方法で調整してみる。Rコンソールでは次の2行を打つだけで済む(多重性の調整をホルム以外の方法でやりたければ,p.adjust.method="bon"などとオプションで指定する)。
> prop.test(table(survey$Clap, survey$W.Hnd))
> pairwise.prop.test(table(survey$Clap, survey$W.Hnd))Rcmdrでは,「統計量」「分割表」「2元表」を選び,行の変数としてClapを選び,列の変数としてW.Hndを選んで[OK]ボタンをクリックすると,カイ二乗検定の結果が表示される。検定の多重性の調整はRcmdrではサポートされていない。
EZRでは,「統計解析」「名義変数の解析」から「分割表の作成と群間の比率の比較(Fisherの正確検定)」を選び,「行の選択」からW.Hnd,「列の変数」からClapを選ぶ。「仮説検定」としてカイ2乗検定とフィッシャーの正確検定の左のボックスにチェックを入れ,カイ2乗検定の連続性補正の下のラジオボタンは「はい」にし,「↓2組ずつの比較(post-hoc検定)は比較する群が1つの場合のみ実施される」の下の「2組ずつの比較(Holmの多重比較)」の左のボックスにチェックを入れてから「OK」ボタンをクリックすると,カイ二乗検定だけではなく,フィッシャーの正確検定でも対比較して検定の多重性の調整をHolmの方法で実施した結果が得られる。なお,Rコンソールでもfmsbパッケージに含まれるpairwise.fisher.test()関数を使えば実行できる。
要因が2つ以上ある場合は、交互作用項も含めて考える必要があり、複雑な話になってくるので、このテキストではごく簡単にだけ触れる。MASSパッケージには、二元配置分散分析に適したデータがいくつか含まれているので、それを利用する。
2つの要因の組み合わせごとに繰り返し数が一致していない場合が多いため、通常は、Type IIIの平方和を使った計算が必要になり、carパッケージのAnova()関数を使うべきである。また、要因の対比順序がRのデフォルトはSASなどと異なるため、options(contrasts=)で対比順序を指定しておく方が良い(このサイトの説明がわかりやすい)。
また、グラフとしては、標準誤差か標準偏差のエラーバーが付いた折れ線グラフを使うと良い。簡単に描画できる関数を定義しておく。
# 二元配置の平均と標準誤差または標準偏差の折れ線グラフを描く関数
length2 <- function(X) { length(subset(X, !is.na(X))) }
twowayplot <- function(VAL, F1, F2, DATASET, TYPE=1, MAIN="") {
if (nchar(MAIN)<1) {
MAINA <- sprintf("Two way plot of means with %s", ifelse(TYPE==1, "se", "sd"))}
else {
MAINA <- MAIN}
MM <- by(DATASET[, deparse(substitute(VAL))],
list(DATASET[, deparse(substitute(F1))], DATASET[, deparse(substitute(F2))]),
mean, na.rm=TRUE)
SD <- by(DATASET[, deparse(substitute(VAL))],
list(DATASET[, deparse(substitute(F1))], DATASET[, deparse(substitute(F2))]),
sd, na.rm=TRUE)
NN <- by(DATASET[, deparse(substitute(VAL))],
list(DATASET[, deparse(substitute(F1))], DATASET[, deparse(substitute(F2))]),
length2)
SE <- SD/sqrt(NN)
XLAB <- levels(DATASET[, deparse(substitute(F1))])
CLAB <- levels(DATASET[, deparse(substitute(F2))])
matplot(MM, pch=16, type="b", col=1:length(CLAB),
xlab=deparse(substitute(F1)), ylab=deparse(substitute(VAL)),
ylim=c(min(MM-SD, na.rm=TRUE), max(MM+SD, na.rm=TRUE)),
lty=1:length(CLAB), lwd=1, axes=FALSE, main=MAINA)
if (TYPE==1) {
arrows(1:length(XLAB), MM-SE, 1:length(XLAB), MM+SE, angle=90, code=3, length=0.1) }
else {
arrows(1:length(XLAB), MM-SD, 1:length(XLAB), MM+SD, angle=90, code=3, length=0.1) }
axis(1, 1:length(XLAB), XLAB)
axis(2)
legend("topright", pch=16, lty=1:length(CLAB), lwd=1, col=1:length(CLAB),
title=deparse(substitute(F2)), legend=CLAB)
return(list(MEAN=MM, SD=SD, SE=SE, N=NN))
}このテキストでは、cabbagesというデータを使って説明する。これは、このテキストのTable 9.5(302ページ)に含まれているデータである。アウトカムとして、収穫したキャベツの重さ(kg単位)が、HeadWtという変数、それに影響を与える要因として、要因1がキャベツの品種(c39/c52)で、Cultという変数、要因2が植え付けた日(d16/d20/d21)でDateという変数に含まれている。
library(car)
options(contrasts = c("contr.sum", "contr.sum"))
# グラフ描画
twowayplot(HeadWt, Date, Cult, cabbages)
# 主効果,交互作用効果とも有意な例
Anova(lm(HeadWt ~ Cult*Date, data=cabbages), type=3)
このコードを実行すると、グラフが描かれ、以下の結果が表示される。
Anova Table (Type III tests)
Response: HeadWt
Sum Sq Df F value Pr(>F)
(Intercept) 403.52 1 856.0629 < 2.2e-16 ***
Cult 5.89 1 12.4969 0.0008451 ***
Date 7.71 2 8.1744 0.0007920 ***
Cult:Date 6.89 2 7.3046 0.0015571 **
Residuals 25.45 54
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
EZRでは、「統計解析」「量的変数の解析」「複数の因子での平均値の比較(多元配置分散分析 multi-way ANOVA)」と選び、目的変数としてHeadWt、因子としてCultとDateを(Ctrlキーを押しながら)選び、「交互作用の解析も行う(群別変数が3個以下の場合)」にチェックが入っていることを確認して「OK」をクリックする。グラフが標準偏差のエラーバー付きの棒グラフになってしまうが、平均と標準偏差、分散分析表が以下のように出力される。現在のバージョンのEZRでは対比順序の設定も自動的にSASと同じ結果を出すように指定されているので、同じ結果が得られる。
Date
Cult d16 d20 d21
c39 3.18 2.80 2.74
c52 2.26 3.11 1.47
Date
Cult d16 d20 d21
c39 0.9566144 0.2788867 0.9834181
c52 0.4452215 0.7908505 0.2110819
Anova Table (Type III tests)
Response: HeadWt
Sum Sq Df F value Pr(>F)
(Intercept) 403.52 1 856.0629 < 2.2e-16 ***
Factor1.Cult 5.89 1 12.4969 0.0008451 ***
Factor2.Date 7.71 2 8.1744 0.0007920 ***
Factor1.Cult:Factor2.Date 6.89 2 7.3046 0.0015571 **
Residuals 25.45 54
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
なお、MASSには、crabsという西オーストラリアの蟹の形態データ(アウトカムは甲羅の前面突起部の幅(mm)を示すFLという変数で、要因は色(青とオレンジ)を示すspという変数と性別(FとM)を示すsexという変数)や、Pima.trという、アリゾナ州フェニックス近くに居住する21歳以上のピマインディアンの女性の糖尿病関連データ(アウトカムはBMIを示すbmiで、要因はWHOの基準による糖尿病判定(No/Yes)を示すtypeという変数と、これまでの妊娠回数がnpregという整数で入っているのをcut(npreg, c(0:2,100), right=FALSE)などして要因型に変えた変数を作り、それら2つを使う)が入っているので、それらでも試してみると良い。
2つの量的な変数間の関係を調べるための,良く知られた方法が2つある。相関と回帰である。いずれにせよ,まず散布図を描くことは必須である。
MASSパッケージのsurveyデータフレームで,身長と利き手の大きさ(親指の先端と小指の先端の距離)の関係を調べるには,Rコンソールでは,require(MASS)としてMASSパッケージをメモリに読み込んだ後であれば,plot(Wr.Hnd ~ Height, data=survey)とするだけである。もし男女別にプロットしたければ,pch=as.integer(Sex)というオプションを指定すれば良い。
EZRでは,「ファイル」「パッケージに含まれるデータを読み込む」から左の枠のMASSでダブルクリックし,右の枠に現れるデータフーレムの下の方へスクロールしてsurveyでダブルクリックしてからOKボタンをクリックした後に,「グラフ」「散布図」と選び,x変数としてHeightを,y変数としてWr.Hndを選び,“最小2乗直線”の左側のチェックボックスのチェックを外し,[OK]をクリックする。男女別にプロット記号を変えたい場合は,「層別のプロット」というボタンをクリックし,層別変数としてSexを選んで[OK]をクリックし,元のウィンドウに戻ったら再び[OK]をクリックすればよい。
大雑把に言えば,相関が変数間の関連の強さ(どの程度大小関係をともにしているか)を表すのに対して,回帰はある変数の値のばらつきがどの程度他の変数の値のばらつきによって説明されるかを示す。回帰の際に,説明される変数を(従属変数または)目的変数,説明するための変数を(独立変数または)説明変数と呼ぶ。2つの変数間の関係を予測に使うためには,回帰を用いる。
一般に,2個以上の変量が「かなりの程度の規則正しさをもって,増減をともにする関係」のことを相関関係(correlation)という。相関には正の相関(positive correlation)と負の相関(negative correlation)があり,一方が増えれば他方も増える場合を正の相関,一方が増えると他方は減る場合を負の相関と呼ぶ。例えば,身長と体重の関係は正の相関である。
散布図で相関関係があるように見えても,見かけの相関関係(apparent correlation)であったり78,擬似相関(spurious correlation)であったり79することがあるので,注意が必要である。
平均と標準偏差と相関係数がまったく同じでも散布図を描くと2つの変数の関係はまったく違う例が、datasauRusというパッケージをインストールして、example(datasaurus_dozen)を実行すればわかる。大阪大学医学部Python会のサイトの記事も大変興味深い。
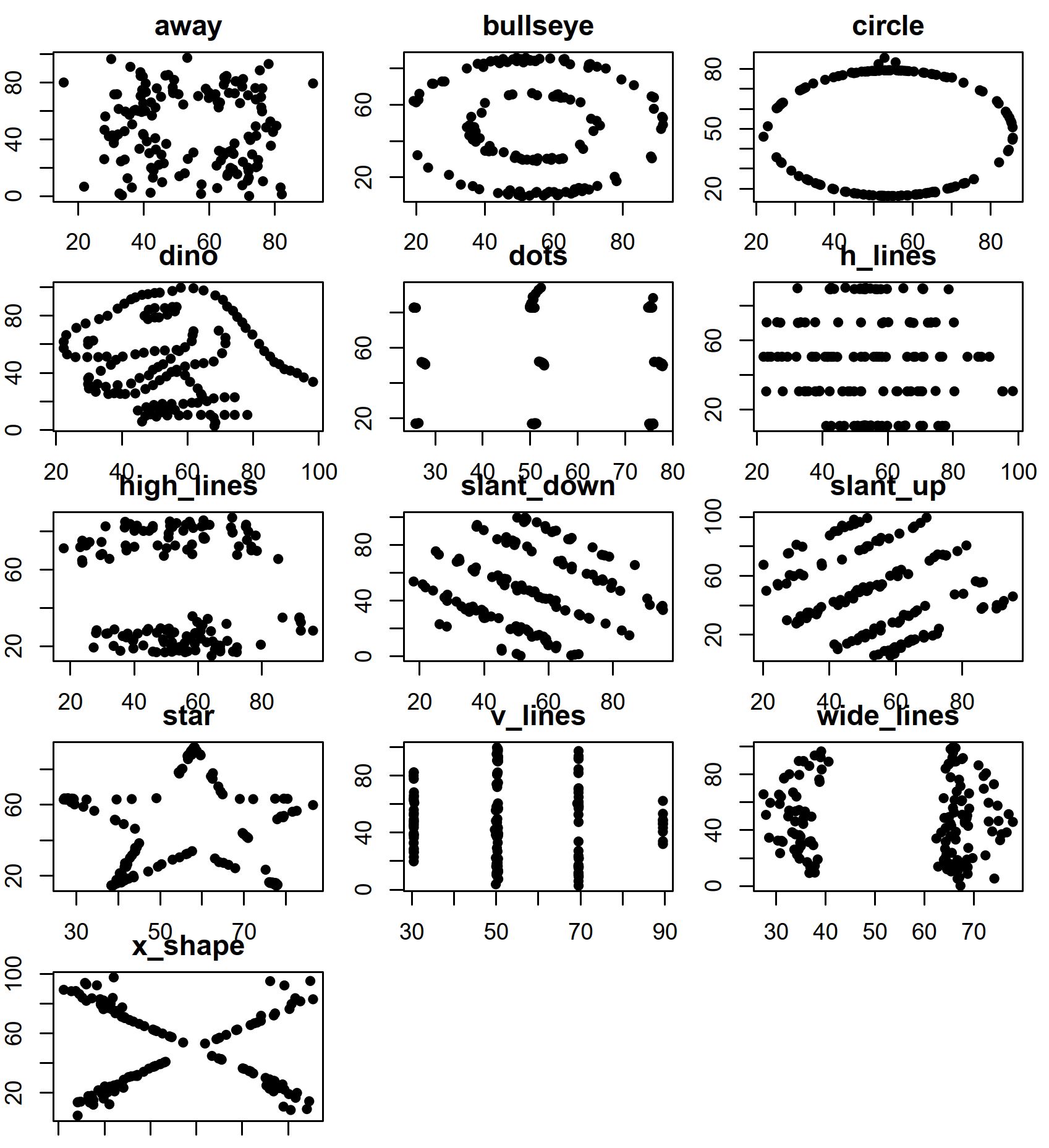
相関関係は増減をともにすればいいので,直線的な関係である必要はなく,二次式でも指数関数でもシグモイドでもよいが,通常,直線的な関係をいうことが多い(指標はピアソンの積率相関係数)。曲線的な関係の場合,直線的になるように変換したり,ノンパラメトリックな相関の指標(順位相関係数)を計算する。順位相関係数としてはスピアマンの順位相関係数が有名である。
ピアソンの積率相関係数(Pearson’s Product Moment Correlation Coefficient)は,rという記号で表し,2つの変数XとYの共分散をXの分散とYの分散の積の平方根で割った値であり,範囲は[ − 1, 1]である。最も強い負の相関があるときr = − 1,最も強い正の相関があるときr = 1,まったく相関がないとき(2つの変数が独立なとき),r = 0となることが期待される。Xの平均をX,Yの平均をYと書けば,次の式で定義される。
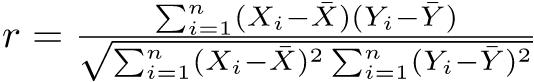
相関係数の有意性の検定においては,母相関係数がゼロ(=相関が無い)という帰無仮説の下で,実際に得られている相関係数よりも絶対値が大きな相関係数が偶然得られる確率(これを「有意確率」という。通常,記号pで表すので,「p値」とも呼ばれる)の値を調べる。偶然ではありえないほど珍しいことが起こったと考えて,帰無仮説が間違っていたと判断するのは有意確率がいくつ以下のときか,という水準を有意水準といい,検定の際には予め有意水準を(例えば5%と)決めておく必要がある。例えばp = 0.034であれば,有意水準5%で有意な相関があるという意思決定を行なうことができる。p値は,検定統計量
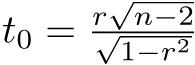 が自由度n − 2のt分布に従うことを利用して求められる。
が自由度n − 2のt分布に従うことを利用して求められる。
散布図を描いたsurveyデータフレームの身長と利き手の大きさの間でピアソンの相関係数を計算し,その有意性を検定するには,Rコンソールでは次の1行を打てばよい(スピアマンの順位相関について実行したい時は,method=spearmanを付ける)。
cor.test(survey$Height, survey$Wr.Hnd)EZRでは,「統計解析」の「連続変数の解析」から「相関係数の検定(Pearsonの積率相関係数)」を選び,変数としてHeightとWr.Hndを選ぶ(キーを押しながら変数名をクリックすれば複数選べる)。検定については「対立仮説」の下に「両側」「相関<0」「相関>0」の3つから選べるようになっているが,通常は「両側」でよい。OKをクリックすると,出力ウィンドウに次の内容が表示される。
Pearson's product-moment correlation
data: survey$Height and survey$Wr.Hnd
t = 10.7923, df = 206, p-value < 2.2e-16
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.5063486 0.6813271
sample estimates:
cor
0.6009909
(中略)
correlation coefficient = 0.601, 95% CI 0.506-0.681, p.value = 8.23e-22EZRの出力は最下行がまとめなので,そこだけ見れば良い。身長と利き手の大きさの関係について求めたピアソンの積率相関係数は,r = 0.601(95%信頼区間が[0.506, 0.681])であり80,p-value < 2.2e-16(有意確率が2.2 × 10 − 16より小さいという意味)より,「相関が無い」可能性はほとんどゼロなので,有意な相関があるといえる。なお,相関の強さは相関係数の絶対値の大きさによって判定し,伝統的に0.7より大きければ「強い相関」,0.4~0.7で「中程度の相関」,0.2~0.4で「弱い相関」とみなすのが目安なので,この結果は中程度の相関を示すといえる。
男女別に相関係数の検定を実行するには,いろいろなやり方があるが,最も単純に考えれば,データセットそのものを男女別の部分集合に分け,それぞれについて分析すればよい。Rコンソールでは次の4行を打つ(その前に,MASSパッケージをメモリに読み込んでおかねばならないのは当然である)。
males <- subset(survey, Sex=="Male")
cor.test(males$Height, males$Wr.Hnd)
females <- subset(survey, Sex=="Female")
cor.test(females$Height, females$Wr.Hnd)EZRでは,相関係数を求めるメニューの下の方にあるボックスにSex=="Male"と入力してから[OK]ボタンをクリックすれば男性の身長と利き手の大きさについてピアソンの積率相関係数を求めて有意性の検定をすることができるし,女性についてもボックスにタイプする文字列を,Sex=="Male"の代わりにSex=="Female"とするだけで良い。
もちろん,相関についてだけ男女別の分析をするなら,データセットの分割をしなくてもいい。Rコンソールなら,
isMale <- (survey$Sex=="Male")
isFemale <- (survey$Sex == "Female")
cor.test(survey$Height[isMale], survey$Wr.Hnd[isMale])
cor.test(survey$Height[isFemale], survey$Wr.Hnd[isFemale])のようにしてもいいし,第一の引数として与える行列やデータフレームを,第二の引数として与える要因型変数で層別したリストとして返す機能をもつsplit()関数を使って,
z <- split(survey[, c("Height", "Wr.Hnd")], survey[, "Sex"])
cor.test(z[[1]]$Height, z[[1]]$Wr.Hnd) # Female
cor.test(z[[2]]$Height, z[[2]]$Wr.Hnd) # Maleのようにしてもいい。あるいは,
cor.testm <- function(MM) {
k <- NCOL(MM)
for (i in 1:(k-1)) {
for (j in (i+1):k) {
print(cor.test(MM[, i], MM[, j]))
}
}
}
lapply(split(survey[, c("Height", "Wr.Hnd")], survey$Sex), cor.testm)のように,行列を引数として,すべての2列ずつの組合せについて相関係数を計算する関数cor.testm()を定義してから,lapplyとsplitを使って1行で分析を完了することもできる。このやり方なら,survey$Sexのところを,例えばsurvey$Smokeにするだけで喫煙状況の層別に相関係数を計算することができる。
RcmdrやEZRのメニューにはまだ入っていないが(jamoviのモジュールにもない),相関関係を図示したい場合,回帰直線を引くのはミスリーディングになるので,集中楕円とか確率楕円と呼ばれる楕円を描画するのが普通である。一般に楕円が細長ければ相関関係が強く,真円に近ければ相関関係はないか,あったとしても弱い(真横や完全に上下に細長い=ばらつきが小さい場合でも,相関関係がないときは,適切にスケーリングすれば散布図は真円に近くなるはずである)。
集中楕円を描く関数は,carという標準パッケージに含まれているdataEllipse()である(散布図を描いて楕円を重ね描きしてくれる)。層別に色を変えて描くこともできる。例えば,身長と利き手の大きさであれば,
library(car)
z <- survey[, c("Height", "Wr.Hnd", "Sex")]
z <- subset(z, complete.cases(z)) # 欠損値があるとdataEllipse()ができない
layout(t(1:2))
dataEllipse(z$Height, z$Wr.Hnd, levels=0.95)
dataEllipse(z$Height, z$Wr.Hnd, z$Sex, levels=0.95)と打てば,身長と利き手の大きさの関係が散布図及び95%の集中楕円として示される。右の図では3番目の引数として性別を与えたために男女層別に楕円が描かれている。
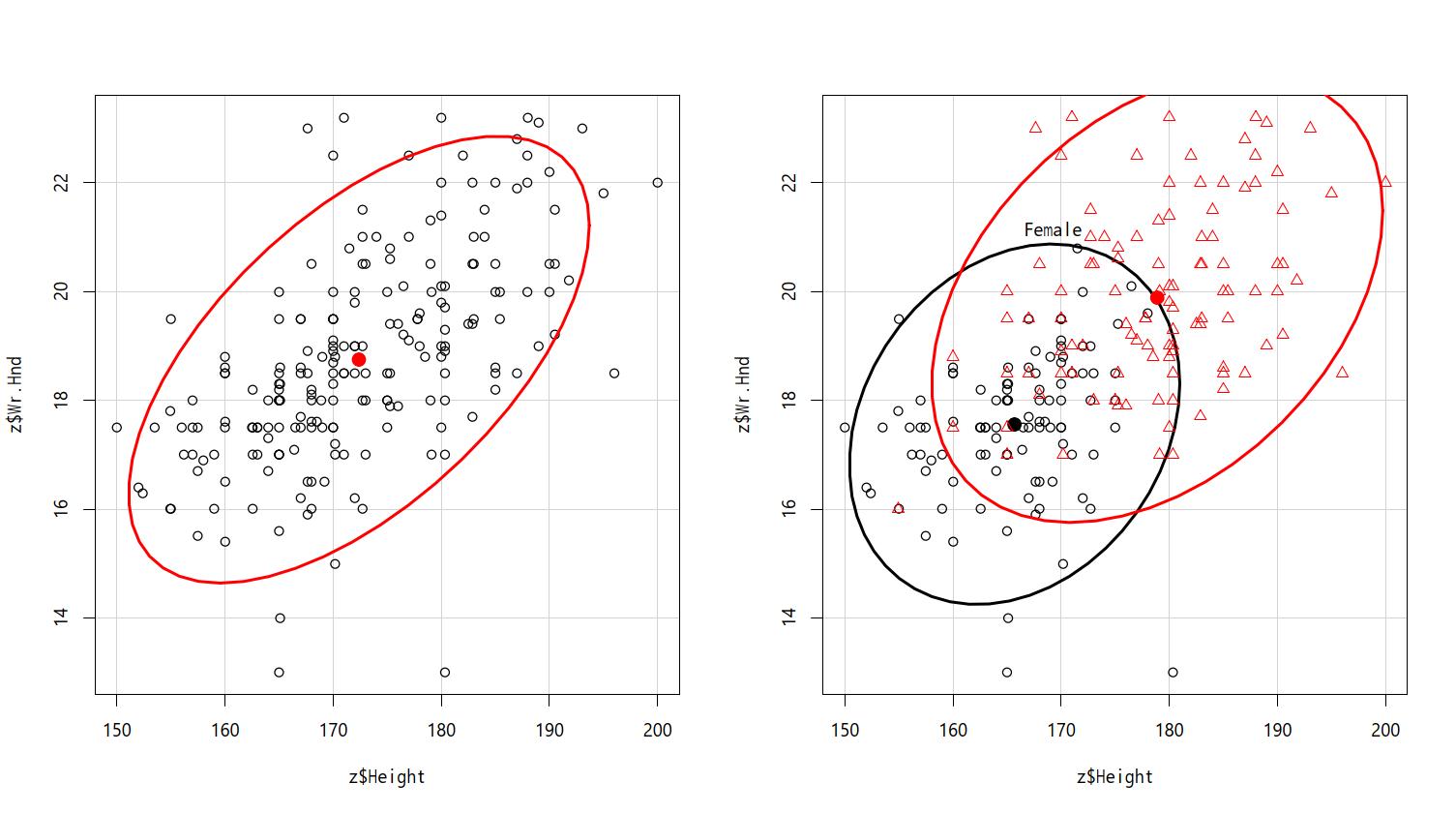
ここで気になってくるのは,「2つの楕円に差が無いかどうか」である。もちろん,この例では身長も利き手の大きさも,明らかに男性の方が女性よりも値が大きいので,検定などするまでもなく,2つの楕円が異なることは明らかだが,もっと微妙な場合もあるだろう。この問題は,HotellingのT2検定という方法で分析できる。Excelで実行する方法81やSASで実行する方法82もインターネット上に公開されているが,簡単に言えば,1つの量的変数について2群間で平均値の差が無いという帰無仮説を検定するt検定(実際はWelchの方法を使うのが普通)を2つ以上の量的変数の比較に拡張しようというアイディアである。数式はミネソタ大学の統計学の資料が見やすい83。
集中楕円は2つの変数について描くので,「2つの集中楕円に差が無いか」をみるためにHotellingのT2検定を使うなら,比べる量的変数は2つで,それらの変数のどちらについても2群間で平均値に差が無いというのが帰無仮説になる。身長と利き手の大きさに性差がないという帰無仮説を検定するには,既に上述のコードで集中楕円を描くためにzという欠損値を除去したデータフレームができていれば,続けて次のコードを実行すればよい。
if (require(Hotelling)==FALSE) {
install.packages("Hotelling", dep=TRUE)
library(Hotelling)
}
Z <- split(z[, c("Height", "Wr.Hnd")], z[, "Sex"])
print(hotelling.test(Z[[1]], Z[[2]]))結果は,検定統計量であるHotellingのT2が108.91,分子の自由度が2(2変数の比較なため),分母の自由度が204(サンプルサイズから比較する変数の個数を引いてさらに1を引いた値)で,最後にP-value: 0と表示されるので,p値が0に近いきわめて小さい値であり,2つの集中楕円には統計学的に有意な差があったといえる。
なお,有意差がない場合もついでに示しておく。surveyデータで男女別に年齢と心拍の関係をプロットし,集中楕円を重ね描きした上で,年齢と心拍について性差がないかHotellingのT2検定をしてみるには,既にMASS, car, Hotellingを読み込んだ後であれば,以下のコードを打てば良い。
z2 <- survey[, c("Age", "Pulse", "Sex")]
z2 <- subset(z2, complete.cases(z2)) # 欠損値除去
dataEllipse(z2$Age, z2$Pulse, z2$Sex, levels=0.95)
Z2 <- split(z2[, c("Age", "Pulse")], z2[, "Sex"])
print(hotelling.test(Z2[[1]], Z2[[2]]))次のグラフが描かれた後に,Test stat: 0.68793,Numerator df: 2,Denominator df: 188,P-value: 0.5039と表示され,このデータについては男女間に統計学的に有意な差があるとはいえないことがわかる。

散布図をみて明らかに外れ値がある場合や,関連が直線的でない場合などは,順位相関係数の適用も検討すべきである。
スピアマンの順位相関係数ρは84,値を順位で置き換えた(同順位には平均順位を与えた)ピアソンの積率相関係数と同じである。Xiの順位をRi,Yiの順位をQiとかけば,
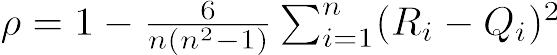 となる。スピアマンの順位相関係数がゼロと差がないことを帰無仮説とする両側検定は,サンプル数が10以上ならばピアソンの場合と同様に,
となる。スピアマンの順位相関係数がゼロと差がないことを帰無仮説とする両側検定は,サンプル数が10以上ならばピアソンの場合と同様に,
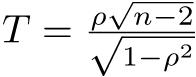 が自由度n − 2のt分布に従うことを利用して行うことができる。ケンドールの順位相関係数τは,
が自由度n − 2のt分布に従うことを利用して行うことができる。ケンドールの順位相関係数τは,
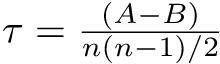 によって得られる。ここでAは順位の大小関係が一致する組の数,Bは不一致数である。
によって得られる。ここでAは順位の大小関係が一致する組の数,Bは不一致数である。
Rコンソールで順位相関係数を計算するには,cor.test()関数のオプションとして,method="spearman"またはmethod="kendall"を指定すれば良い。
EZRでは,「統計解析」「ノンパラメトリック検定」「相関係数の検定(Spearmanの順位相関係数)」から,解析方法のところでSpearmanかKendallの横のラジオボタンを選んでOKボタンをクリックすれば計算できる。
ただし,cor.test()関数やRcmdr/EZR/jamoviでは,順位相関係数の信頼区間は表示されない。xとyの相関を求めるとき,cor.test(x, y, method="spearman")は,ρそのものはcor(rank(x), rank(y))で求めている(getS3method("cor.test", "default")で内部コードを見るとわかる)。けれども,ρをz変換したものが近似的に正規分布に従うと仮定しないとcor.test(rank(x), rank(y))の結果表示される信頼区間がρの信頼区間にはならないので,そう言い切ってしまうのは抵抗を感じる85。おそらくbootstrapで求めるのが原理的には正しいやり方であり,追加パッケージをインストールすることで実行可能になる。スピアマンの順位相関係数の信頼区間は,RVAideMemoireパッケージのspearman.ci()関数で求めることができる。bootstrapの回数はnrep=オプションで指定するが,通常は1000もあれば良い。ケンドールの順位相関係数τの信頼区間は,NSM3パッケージのkendall.ci()関数で得られる。bootstrap=FALSEオプションを与えると(それがデフォルト)近似値が得られ,bootstrapするときは,bootstrap=TRUEオプションを付け,B=オプションで回数を指定する。以下に,アメリカ桜のサイズデータであるtreesにおける,樹高Heightと体積Volumeの相関を検討する例を示す。bootstrapは数値シミュレーションなので,実行するたびに若干違う結果になるが,近似計算よりも幅が広めに出るようである。
なお、DescToolsパッケージのKendallTauB()関数でconf.level=オプションを付けて使えば、ケンドールの順位相関係数の点推定量とフィッシャーのZ変換を使って得られる近似的な信頼区間が同時に得られる。欠損値を含むデータにも対応しているし、動作が軽いので、通常はこれで十分だと思う。
data(trees)
plot(trees$Height, trees$Volume) # 散布図は,やや下に凸な正の相関にみえる
cor.test(trees$Height, trees$Volume, method="spearman")
cor.test(rank(trees$Height), rank(trees$Volume), method="pearson")
library(RVAideMemoire)
spearman.ci(trees$Height, trees$Volume, nrep=1000)
cor.test(trees$Height, trees$Volume, method="kendall")
library(NSM3)
kendall.ci(trees$Height, trees$Volume, bootstrap=FALSE)
kendall.ci(trees$Height, trees$Volume, bootstrap=TRUE, B=1000)ちなみに,SASのPROC CORRの方法86でスピアマンの順位相関係数と信頼区間を計算する関数は,次のように定義できる。既にfmsbパッケージに入れてあるので入力しなくても使える。
spearman.ci.sas <- function(x, y, adj.bias=TRUE, conf.level=0.95) {
NAMEX <- deparse(substitute(x))
NAMEY <- deparse(substitute(y))
xx <- subset(x, !is.na(x)&!is.na(y))
y <- subset(y, !is.na(x)&!is.na(y))
x <- xx
n <- length(x)
rx <- rank(x)
ry <- rank(y)
mx <- mean(rx)
my <- mean(ry)
rho <- sum((rx-mx)*(ry-my))/sqrt(sum((rx-mx)^2)*sum((ry-my)^2))
adj <- ifelse(adj.bias, rho/(2*(n-1)), 0)
z <- 1/2*log((1+rho)/(1-rho))
gg <- qnorm(1-(1-conf.level)/2)*sqrt(1/(n-3))
ge <- z - adj
gl <- ge - gg
gu <- ge + gg
rl <- (exp(2*gl)-1)/(exp(2*gl)+1)
re <- (exp(2*ge)-1)/(exp(2*ge)+1)
ru <- (exp(2*gu)-1)/(exp(2*gu)+1)
cat(sprintf("Spearman's rank correlation between %s and %s\n", NAMEX, NAMEY))
cat(sprintf("N= %d, rho = %5.3f, %2d%% conf.int = [ %5.3f, %5.3f ]\n",
n, re, conf.level*100, rl, ru))
return(list(X=NAMEX, Y=NAMEY, N=n, rho=re, rho.ll=rl, rho.ul=ru, adj.bias=adj.bias))
}回帰は,従属変数のばらつきを独立変数のばらつきで説明するというモデルの当てはめである。十分な説明ができるモデルであれば,そのモデルに独立変数の値を代入することによって,対応する従属変数の値が予測あるいは推定できるし,従属変数の値を代入すると,対応する独立変数の値が逆算できる。こうした回帰モデルの実用例の最たるものが検量線である。検量線とは,実験において予め濃度がわかっている標準物質を測ったときの吸光度のばらつきが,その濃度によってほぼ完全に(通常98%以上)説明されるときに(そういう場合は,散布図を描くと,点々がだいたい直線上に乗るように見える),その関係を利用して,サンプルを測ったときの吸光度からサンプルの濃度を逆算するための回帰直線である(曲線の場合もあるが,通常は何らかの変換をほどこし,線形回帰にして利用する)。
検量線の計算には,(A)試薬ブランクでゼロ点調整をした場合の原点を通る回帰直線を用いる場合と,(B)純水でゼロ点調整をした場合の切片のある回帰直線を用いる場合がある。例えば,濃度の決まった標準希釈系列(0, 1, 2, 5, 10 μg/ℓ)について,純水でゼロ点調整をしたときの吸光度が,(0.24, 0.33, 0.54, 0.83, 1.32)だったとしよう。吸光度の変数をy,濃度をxと書けば,回帰モデルはy = bx + aとおける。係数aとb(aは切片,bは回帰係数と呼ばれる)は,次の偏差平方和を最小にするように,最小二乗法で推定される。
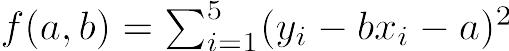
この式を解くには,f(a, b)をaないしbで偏微分したものがゼロに等しいときを考えればいいので,次の2つの式が得られる。
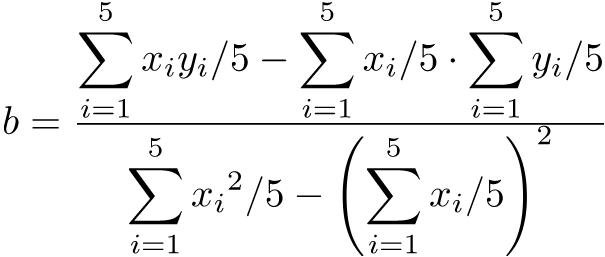
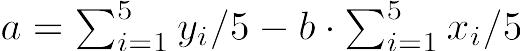
これらのaとbの値と,未知の濃度のサンプルについて測定された吸光度(例えば0.67としよう)から,そのサンプルの濃度を求めることができる。注意すべきは,サンプルについて測定された吸光度が,標準希釈系列の吸光度の範囲内になければならないことである。回帰モデルが標準希釈系列の範囲外でも直線性を保っている保証は何もないのである87。
Rコンソールでは,lm()(linear modelの略で線形モデルの意味)を使って,次のようにデータに当てはめた回帰モデルを得ることができる。
y <- c(0.24, 0.33, 0.54, 0.83, 1.32)
x <- c(0, 1, 2, 5, 10)
res <- lm(y ~ x) # 線形回帰モデルを当てはめ
summary(res) # 詳しい結果表示
plot(y ~ x) # 散布図を表示
abline(res) # 回帰直線を重ね描き
AB <- coef(res) # 切片と回帰係数を取り出す
(0.67 - AB[1])/AB[2] # 吸光度0.67に対応する濃度を計算上枠内の「詳しい結果」は次のように得られる。
Call:
lm(formula = y ~ x)
Residuals:
1 2 3 4 5
-0.02417 -0.04190 0.06037 0.02718 -0.02147
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 0.26417 0.03090 8.549 0.003363 **
x 0.10773 0.00606 17.776 0.000388 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.04894 on 3 degrees of freedom
Multiple R-squared: 0.9906, Adjusted R-squared: 0.9875
F-statistic: 316 on 1 and 3 DF, p-value: 0.0003882推定された切片はa = 0.26417,回帰係数はb = 0.10773である。また,このモデルはデータの分散の98.75% (0.9875)を説明していることが,Adjusted R-squaredからわかる。また,p-valueは,吸光度の分散がモデルによって説明される程度が誤差分散によって説明される程度と差が無いという帰無仮説の検定の有意確率である。

0.67という吸光度に相当する濃度は,3.767084となる。したがって,この溶液の濃度は,3.8 μg/ℓだったと結論することができる。
EZRでは,データはデータフレームとして入力しなくてはいけない(もちろん,Excelなどで入力して読み込んでも良いが)。「ファイル」「新しいデータセットを作成する」を選び,データセット名を入力:と書かれたテキストボックスにworkingcurveと打って[OK]ボタンをクリックする。データエディタウィンドウが表示されたら,[var1]をクリックして,変数エディタの変数名というテキストボックスにyと打ち,型として“numeric”の方のラジオボタンをクリックしてから,キーボードのキーを押す。次いで,同様にして[var2]を[x]に変える。それから,それぞれのセルに吸光度と濃度のデータを入力し,データエディタウィンドウを閉じる(通常は「ファイル」「閉じる」を選ぶ)。
散布図と回帰直線を描くには,「グラフと表」「散布図」を選んで,x変数としてxを,y変数としてyを選び,[OK]ボタンをクリックする。
線形回帰モデルを当てはめるには,「統計解析」「連続変数の解析」「線形回帰(単回帰,重回帰)」と選び,目的変数としてy,説明変数としてxを選び,「モデル解析用に解析結果をアクティブモデルとして残す」の左のチェックボックスにチェックを入れて[OK]をクリックする。アウトプットウィンドウに結果が表示される(後述する多重共線性をチェックするためにVIFを計算しようとしてエラーが表示されるが気にしなくて良い)。
検量線以外の状況でも,同じやり方で線形回帰モデルを当てはめることができる。 surveyデータフレームに戻ってみよう(もちろん,surveyデータセットを使う前には,MASSパッケージをロードしておく必要がある)。もし利き手の幅の分散を身長によって説明したいなら,線形回帰モデルを当てはめるには,Rコンソールでは次のようにタイプすればいい。
res <- lm(Wr.Hnd ~ Height, data=survey)
summary(res)EZRでは,ロゴのすぐ右の“データセット:”の右側をクリックしてsurveyを指定し,surveyデータセットをアクティブにしてから,「統計量」「モデルへの適合」「線形回帰」と選び,目的変数としてWr.Hnd,説明変数としてHeightを選び,「モデル解析用に解析結果をアクティブモデルとして残す」の左のチェックボックスにチェックを入れてから[OK]をクリックすると結果が得られる。
回帰直線のパラメータ(回帰係数bと切片a)の推定値の安定性を評価するためには,t値が使われる。いま,YとXの関係がY = a0 + b0X + eというモデルで表されるとして,誤差項eが平均0,分散σ2の正規分布に従うものとすれば,切片の推定値aも,平均a0,分散(σ2/n)(1 + M2/V)(ただしMとVはxの平均と分散)の正規分布に従い,残差平方和Qを誤差分散σ2で割ったQ/σ2が自由度(n − 2)のカイ二乗分布に従うことから,
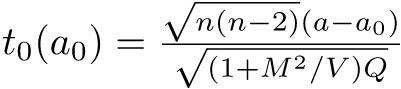 が自由度(n − 2)のt分布に従うことになる。
が自由度(n − 2)のt分布に従うことになる。
しかしこの値はa0がわからないと計算できない。a0が0に近ければこの式でa0 = 0と置いた値(つまりt0(0)。これを切片に関するt値と呼ぶ)を観測データから計算した値がt0(a0)とほぼ一致し,自由度(n − 2)のt分布に従うはずなので,その絶対値は95%の確率でt分布の97.5%点(サンプルサイズが大きければ約2である)よりも小さくなる。つまり,データから計算されたt値がそれより大きければ,切片は0でない可能性が高いことになるし,t分布の分布関数を使えば,「切片が0である」という帰無仮説に対する有意確率が計算できる。
回帰係数についても同様に,
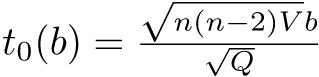 が自由度(n − 2)のt分布に従うことを利用して,「回帰係数が0」であるという帰無仮説に対する有意確率が計算できる。有意確率が充分小さければ,切片や回帰係数がゼロでない何かの値をとるといえるので,これらの推定値は安定していることになる。
が自由度(n − 2)のt分布に従うことを利用して,「回帰係数が0」であるという帰無仮説に対する有意確率が計算できる。有意確率が充分小さければ,切片や回帰係数がゼロでない何かの値をとるといえるので,これらの推定値は安定していることになる。
RコンソールでもEZRでも,線形回帰をした結果の中の,Pr(>|t|)というカラムに,これらの有意確率が示されている。
説明変数は2つ以上の変数を含むことができる。このような場合,モデルは「重回帰モデル」と呼ばれる。 注意しなくてはならない点がいくつかあるが,基本的には線形モデルの右側に+でつないで説明変数群を与えるだけである。
例えば,これまで扱ってきたsurveyデータで,利き手の大きさの分散を説明するために,身長のみならず,利き手でない方の手の大きさも使うことにしよう。Rコンソールでは次のように打てばよい(もちろん,予めMASSパッケージをロードしておかねばならない)。
res <- lm(Wr.Hnd ~ Height + NW.Hnd, data=survey)
summary(res)EZRでは,まず「アクティブデータセット」の下の枠をクリックしてsurveyを選び直してから,「統計解析」「連続変数の解析」「線形回帰(単回帰,重回帰)」を選び,“目的変数”としてWr.Hndをクリックし,“説明変数”としてHeightをクリックしてからキーボードのキーを押しながらNW.Hndもクリックし,「モデル解析用に解析結果をアクティブモデルとして残す」の左のチェックボックスにチェックを入れてから[OK]ボタンをクリックすると,結果がアウトプットウィンドウに示される。
アウトプットウィンドウを少し上にスクロールすると,後述する多重共線性の指標値であるVIFの値も計算されているので,10を超えるような値になっていないか確認するべきである。
重回帰モデルでは,個々の説明変数について推定される回帰係数は,他の説明変数の目的変数への影響を調整した上で,その変数独自の目的変数への影響を示す「偏回帰係数」である。しかし偏回帰係数の値は,各変数の絶対的な大きさに依存しているので,各説明変数の目的変数への影響の相対的な強さを示すものにはならない。そうした比較をしたければ,Rコンソールで次のようにタイプしてstbとして得られる「標準化偏回帰係数」が利用できる。結果をみると,Heightの標準化偏回帰係数が0.058,NW.Hndの標準化偏回帰係数が0.929なので,利き手の大きさは大部分,利き手でない手の大きさによって説明されることがわかる。
# res <- lm(Wr.Hnd ~ Height + NW.Hnd, data=survey) # の実行後に
csd <- sapply(res$model, sd) # res$modelの各変数のsdを計算
print(coef(res)*csd/csd[1]) # 標準化偏回帰係数EZRには,メニューアイテムとしては,この機能は提供されていない。しかし,重回帰モデルを「残して」あるので,そのオブジェクトを使ったコマンドをスクリプトウィンドウに打つ。右上に「モデル:」とあるところの右側に,最後に生成されたモデル名が表示されている。これがRegModel.1だとすると,上の3行の前に,res <- RegModel.1という1行を追加すれば良い。その4行を選んでから,「実行」ボタンをクリックすれば,結果がアウトプットウィンドウに表示される。
なお,標準化偏回帰係数の代わりに,偏相関係数の二乗を使っても,それぞれの説明変数の目的変数への影響の相対的な寄与を示すことができる(Residualsの項を除く,すべての説明変数の偏相関係数の二乗を合計すると,次節で説明する重相関係数の二乗—ただし当然ながら自由度調整する前の値—になる)。最近の論文では,重回帰分析の結果の表としては,各説明変数に対して,偏回帰係数,標準誤差,95%信頼区間の下限と上限,偏相関係数の二乗を示すことが多いように思う。偏相関係数の二乗を求めるには,RegModel.1に重回帰分析結果が付値されているとすると,下記の2行を実行すれば良い。
SS <- anova(RegModel.1)["Sum Sq"]
SS/sum(SS)以下の結果が得られる。
Sum Sq
Height 0.36119012
NW.Hnd 0.56830022
Residuals 0.07050966偏相関係数の二乗は,他の変数の影響を調整した上で,それぞれの変数のばらつきが目的変数のばらつきのどれくらいの割合に寄与しているか(説明するか)を意味していると解釈することができるので,標準化偏回帰係数よりも意味がわかりやすいかもしれない。
なお,r族の効果量として触れたηp2は,ウィスコンシン大学で開発されていたlmSupportパッケージに含まれているmodelEffectSizes()関数で計算させることができたが,既にcranから消滅しているので,現在では,以下のようにlsrパッケージのetaSquared()関数か,heplotsパッケージのetasq()関数を使うと良い(コードと結果をまとめて示す)。
> library(lsr)
> etaSquared(res)
eta.sq eta.sq.part
Height 0.002251836 0.03094818
NW.Hnd 0.568300223 0.88962341
> library(heplots)
> etasq(res, anova=TRUE)
Anova Table (Type II tests)
Response: Wr.Hnd
Partial eta^2 Sum Sq Df F value Pr(>F)
Height 0.03095 1.69 1 6.547 0.01123 *
NW.Hnd 0.88962 426.25 1 1652.278 < 2e-16 ***
Residuals 52.88 205
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1一般に,複数の独立変数がある場合の回帰で,独立変数同士に強い相関があると,重回帰モデルの係数推定が不安定になるのでうまくない。
ごく単純な例でいえば,従属変数Yに対して独立変数群X1とX2が相加的に影響していると考えられる場合,lm(Y ~ X1+X2)という重回帰モデルを立てるとしよう。ここで,実はX1がX2と強い相関をもっているとすると,もしX1の標準化偏回帰係数の絶対値が大きければ,X2による効果もそちらで説明されてしまうので,X2の標準化偏回帰係数の絶対値は小さくなるだろう。まったくの偶然で,その逆のことが起こるかもしれない。したがって,係数推定は必然的に不安定になる。
この現象は,独立変数群が従属変数に与える線型の効果を共有しているという意味で,多重共線性(multicolinearity)と呼ばれる。
多重共線性があるかどうかを判定するには,独立変数間の散布図を1つずつ描いてみるなど,丁寧な吟味をすることが望ましいが,各々の独立変数を,それ以外の独立変数の従属変数として重回帰モデルを当てはめたときの重相関係数の2乗を1から引いた値の逆数をVIF(Variance Inflation Factor; 定訳は不明だが,分散増加因子と訳しておく)として,VIFが10を超えたら多重共線性を考えねばならないという基準を使う(Armitage et al., 2002)のが簡便である。
多重共線性があるときは,拡張期血圧(DBP)と収縮期血圧(SBP)のように本質的に相関があっても不思議はないものだったら片方だけを独立変数に使うとか,2つの変数を使う代わりに両者の差である脈圧を独立変数として使うのが1つの対処法だが,その相関関係自体に交絡が入る可能性はあるし,情報量が減るには違いない。
変数を減らさずに調整する方法としては,centringという方法がある。リッジ回帰(RではMASSパッケージのlm.ridge())によっても対処可能である。
また,DAAGパッケージ(Maindonald and Braun, 2003)のvif()関数を使えば,自動的にVIFの計算をさせることができる88。既に述べた通りEZRでは重回帰分析を行うと自動的にVIFは計算されている。fmsbパッケージのVIF()関数を使うこともできるが,vif()関数とは使い方が違うので注意が必要である。
データから得た回帰直線は,完璧にデータに乗ることはない。そこで,回帰直線の当てはまりの良さを評価する。aとbが決まったとして,zi = a + bxiとおいたとき,ei = yi − ziを残差(residual)と呼ぶ。残差は,yiのばらつきのうち,回帰直線では説明できなかった残りに該当する。つまり,残差が大きいほど,回帰直線の当てはまりは悪いと考えられる。残差にはプラスもマイナスもあるので二乗和をとり,次の式で得られる「残差平方和」Qを定義することができる。

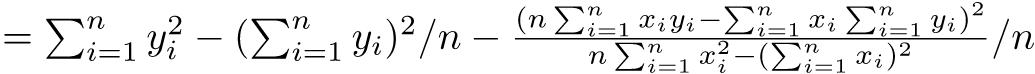
残差平方和Qは回帰直線の当てはまりの悪さを示す尺度であり,それをnで割ったQ/nを残差分散という。残差分散(var(e)と書くことにする)とYの分散var(Y)とピアソンの相関係数rの間には, var(e) = var(Y)(1 - r2) という関係が常に成り立つので, r2 = 1 - var(e)/var(Y) となる。このことからr2が1に近いほど回帰直線の当てはまりがよいことになる。その意味で,r2を「決定係数」と呼ぶ。また,決定係数は,Yのばらつきがどの程度Xのばらつきによって説明されるかを意味するので,Xの「寄与率」と呼ぶこともある。
データによっては,何通りもの回帰直線の残差平方和が大差ないという状況がありうる。例えば,目的変数と説明変数が実はまったく無関係であった場合は,データの重心を通るどのような傾きの線を引いても残差平方和はほとんど同じになってしまう。言い換えれば,傾きや切片の推定値が不安定になる。
r2は説明変数が多ければ大きくなるので,通常は自由度でr2を調整した「自由度調整済み重相関係数の二乗」を決定係数と考える。この値は,RコンソールでもEZRでも線形モデルの当てはめ結果の中で,Adjusted R-Squared:として表示されている。
当てはまりの良さの別の尺度として,AIC(赤池の情報量基準:Akaike information criterion)も良く用いられる。とくに重回帰モデルでは,AICも表示するのが普通である。RにはAIC()という関数があり,線形回帰モデルの結果を付値したオブジェクトを,この関数に渡せばAICが計算される(例えばAIC(res)のように使う)。ここではAICについて詳しくは説明しないが,たくさんのオンライン資料や書籍で説明されている。
EZRでAICを求めるには,標準化偏回帰係数を求めたときと同様に,スクリプトウィンドウに必要な関数を打ち,それを選択した上で「実行」ボタンをクリックする。モデルがRegModel.1であれば,必要な関数は,AIC(RegModel.1)である。
最小二乗推定の説明から自明なように,回帰式の両辺を入れ替えた回帰直線は一致しない。身長と体重のように,どちらも誤差を含んでいる可能性がある測定値である場合には,一方を説明変数,他方を目的変数とすることは妥当でないかもしれない89。どちらを目的変数とみなし,どちらを説明変数とみなすか,因果関係の方向性に基づいて(先行研究や臨床的知見から)きちんと決めることは重要である。
回帰を使って予測をするとき,外挿には注意が必要である。とくに検量線は外挿してはいけない。実際に測った濃度より濃かったり薄かったりするサンプルに対して,同じ関係が成り立つという保証はどこにもない90。サンプルを希釈したり濃縮したりして,検量線の範囲内で定量しなくてはいけない。
例題 組み込みデータairqualityは,1973年5月1日から9月30日まで154日間のニューヨーク市の大気環境データである。含まれている変数は,Ozone(ppb[=10億分の1]単位でのオゾン濃度),Solar.R(セントラルパークでの8:00から12:00までの4000から7700オングストロームの周波数帯の太陽放射の強さをLangley単位で表した値),Wind(LaGuardia空港で7:00と10:00に測定した平均風速,マイル/時),Temp(華氏での日最高気温),Month(月),Day(日)である。日照の強さを説明変数,オゾン濃度を目的変数として回帰分析せよ。
Rコンソールでは,次の4行で良い。
plot(Ozone ~ Solar.R, data=airquality)
res <- lm(Ozone ~ Solar.R, data=airquality)
abline(res)
summary(res)EZRでは,まず「ファイル」「パッケージに含まれるデータを読み込む」から左の枠のdatasetsをダブルクリックし,右の枠に現れるデータフーレムの下の方へスクロールしてairqualityをダブルクリックしてからOKボタンをクリックしてairqualityデータフレームをアクティブにする。次いで「グラフと表」「散布図」を選び,x変数をSolar.R,y変数をOzoneとして[OK]をクリックする。次に,「統計解析」「連続変数の解析」「線形回帰」を選ぶ。目的変数としてOzoneを,説明変数としてSolar.Rを選んでOKボタンをクリックする。
RコンソールでもEZRでも得られる結果は同じで,次の枠内の通りである。
Call:
lm(formula = Ozone ~ Solar.R, data = airquality)
Residuals:
Min 1Q Median 3Q Max
-48.292 -21.361 -8.864 16.373 119.136
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 18.59873 6.74790 2.756 0.006856 **
Solar.R 0.12717 0.03278 3.880 0.000179 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 31.33 on 109 degrees of freedom
(42 observations deleted due to missingness)
Multiple R-Squared: 0.1213, Adjusted R-squared: 0.1133
F-statistic: 15.05 on 1 and 109 DF, p-value: 0.0001793 得られた回帰式はOzone = 18.599 + 0.127 Solar.Rであり,最下行をみるとF検定の結果のp値が0.0001793ときわめて小さいので,モデルの当てはまりは有意である。しかし,その上の行のAdjusted R-squaredの値が0.11ということは,このモデルではオゾン濃度のばらつきの10%余りしか説明されないことになり,あまりいい回帰モデルではない。
当てはまりを改善するには,説明変数を追加することが有効な場合がある。この例では,WindあるいはTempを説明変数に加えて重回帰モデルにすれば,当てはまりが改善する。Rコンソールでは,次の3行を打てば重回帰モデルの当てはめができる。自由度調整済み重相関係数の二乗が約60%にまで改善していることがわかる。
mres <- lm(Ozone ~ Solar.R + Wind + Temp, data=airquality)
summary(mres)
AIC(mres)変数を追加していったときに有意に当てはまりが改善したかどうかは,尤度比検定によって判定できる。この場合なら,以下のコードを実行すれば良い
res1 <- lm(Ozone ~ Solar.R, data=airquality)
res2 <- lm(Ozone ~ Solar.R + Wind, data=airquality)
res3 <- lm(Ozone ~ Solar.R + Wind + Temp, data=airquality)
anova(res1, res2, res3)OzoneをSolar.Rだけで説明するモデルに比べ,Windを加えたモデルのF値は89.1でp値は9.5×10-16,Solar.RとWindで説明するモデルに比べ,Tempを加えたモデルのF値は42.5でp値は2.4×10-9と,それぞれ有意に当てはまりが改善していることがわかる。
EZRでは,「統計解析」「連続変数の解析」「線形回帰」を選ぶ。“目的変数”としてOzoneを選び,“説明変数”としてSolar.Rをクリックしてからキーボードのキーを押しながらWindとTempもクリックし,「モデル解析用に解析結果をアクティブモデルとして残す」の左のチェックボックスにチェックを入れてから[OK]ボタンをクリックすると,同じ結果が得られる。
目的変数が同じで説明変数が異なる複数の回帰分析の結果をまとめて表示したいことがある。
経済学や社会学の論文を読んでいると頻繁に見かける。この表示をするために便利なパッケージがstargazerである。html形式やLaTeX形式でも出力させることができるが,プレインテキストでも可能である。
それぞれ,オプションとしてtype="html",type="html",type="text"を付ければ良い。デフォルトはLaTeX形式である。
この大気中オゾン濃度の回帰分析の場合,以下のコードを実行すると,その下の表を生成するためのLaTeXコードが表示される。
res1 <- lm(Ozone ~ Solar.R, data=airquality)
res2 <- lm(Ozone ~ Solar.R + Wind, data=airquality)
res3 <- lm(Ozone ~ Solar.R + Wind + Temp, data=airquality)
library(stargazer)
stargazer(res1, res2, res3)
複数のグループがあって,どのグループに属するサンプルについても,同じ説明変数と目的変数が調べられているとき,それらの関係がグループによって異なるかどうか調べたい場合がある。共分散分析は,このような場合に用いられ,典型的なモデルは, Y = β0 + β1 C + β2 X + β12 CX + ε となる。ここで,Cはグループを示す2値変数,XとYは量的な変数(連続変数)である。Cの2群間でYの平均値に差があるかどうかを比べたいのだが,YがXによって影響を受ける場合(Xが共変量である場合),XとYの回帰直線の傾き(slope)がCの2群間で差がないなら,Xによる影響を調整したYの修正平均(adjusted mean; 調整平均ともいう)を,Cの2群間で比べる91。ただし,2本の回帰直線がともに充分な説明力をもっていて,かつ2本の回帰直線の間で傾きに差がない場合でないと,修正平均の比較には意味がない。そもそも回帰直線の説明力が低ければその変数は共変量として考慮する必要がないし,傾きが違っていれば群分け変数と独立変数の交互作用が従属変数に関して有意に影響しているということなので,2群を層別して別々に解釈する方が良い。
いま,Cで群分けされる2つの母集団における,(X, Y)の間の母回帰直線を,y = α1 + β1x,y = α2 + β2xとすれば,共分散分析は次の手順で進める。
例題
https://minato.sip21c.org/grad/sample3.datは,都道府県別のタブ区切りテキストデータファイルである。変数としては,都道府県名(PREF),日本の東西(REGION),1990年の100世帯当たり乗用車台数(CAR1990),1989年の人口10万人当たり交通事故死者数(TA1989),1985年の国勢調査による人口集中地区居住割合(DIDP1985)が含まれている(REGIONの1は東日本,2は西日本を意味する)。
このデータについて,東日本と西日本で,100世帯当たり乗用車台数で調整した人口10万人当たり交通事故死者数に差があるか,共分散分析によって検討せよ93。
Rコンソールでの実行例を示す。
sample3 <- read.delim("https://minato.sip21c.org/grad/sample3.dat")
plot(TA1989 ~ CAR1990, pch=as.integer(REGION), data=sample3,
xlab="Number of cars per 100 households",
ylab="Deaths by traffic accident per 100,000")
east <- subset(sample3,REGION=="East")
regeast <- lm(TA1989 ~ CAR1990, data=east)
summary(regeast)
west <- subset(sample3,REGION=="West")
regwest <- lm(TA1989 ~ CAR1990, data=west)
summary(regwest)
abline(regeast,lty=1)
abline(regwest,lty=2)
legend("bottomright",pch=1:2,lty=1:2,legend=c("East Japan","West Japan"))
summary(lm(TA1989 ~ REGION*CAR1990, data=sample3))
anacova <- lm(TA1989 ~ REGION+CAR1990, data=sample3)
summary(anacova)
cfs <- dummy.coef(anacova)
cfs[[1]] + cfs$CAR1990 * mean(sample3$CAR1990) + cfs$REGION
最後のモデルのREGIONの係数がゼロと差が無いという帰無仮説の検定のp値は,0.0319である。このことから,CAR1990の影響を調整した上でもTA1989には,東日本と西日本の間に,有意水準5%で統計学的に有意な差があると言える。最後の2行によって,東日本,西日本それぞれの,修正平均値は,次のように表示される。
East West
9.44460 10.96650
Rcmdrでは,まずデータセット名sample3としてインターネットからデータを読み込むため,「データ」「データのインポート」「テキストファイル,クリップボードまたはURLから読み込み...」を選び,“データセット名を入力”の右にあるテキストボックスにsample3と打ち,“インターネットURL”の隣のラジオボタンをチェックし,“フィールド区切り”の「タブ」の隣のラジオボタンをチェックし,[OK]ボタンをクリックする。表示されるウィンドウでhttps://minato.sip21c.org/grad/sample3.datと打ち,[OK]をクリックすると,インターネットからデータが読み込まれ,sample3という名前のデータフレームがアクティブになる。
次にREGIONで層別した散布図を描く。「x変数」をCAR1990,「y変数」をTA1989とし,“平滑線”の隣のチェックを外して[OK]し,「グループ別にプロット」をクリックしてREGIONを選んで[OK]し,元のウィンドウでも[OK]すると,散布図と2本の回帰直線が描かれ,2本の回帰直線はほぼ平行に見える(丁寧にやるには,ここで東西日本別々に層別して,CAR1990によってTA1989が説明されるかをみるため,単回帰分析を行う。東日本のサブセットと西日本のサブセットを作って分析すればよい。CAR1990の係数は東西どちらでも有意にゼロと異なる。したがって,その影響を調整することに意味はあると思われることが確認できる)。
次に,傾きに差があるかを解析する。「統計量」「モデルへの適合」「線形モデル」でモデル名LinearModel.3として左辺の目的変数としてTA1989を,右辺の説明変数群としてREGION+CAR1990+REGION:CAR1990を指定する。結果をみると,REGIONWest:CAR1990の行に示されている交互作用効果のp値は0.990である。この値は,2本の回帰直線の傾きに統計学的な有意差がないことを意味する。
そこで今度は,乗用車所有台数で調整した交通事故死者数の修正平均に差があるかどうかをみるため,交互作用項を除いて回帰を行う。再び「統計量」「モデルへの適合」「線形モデル」で,モデル名をLinearModel.4とし,左辺はそのままTA1989で,右辺の説明変数をCAR1990+REGIONに変えて線形モデルの当てはめを実行する。この結果,REGIONWestの行のp値は0.0319なので,REGIONという変数は,有意水準5%で,CAR1990の影響を調整してもTA1989に対して統計学的に有意な影響をもっていることが示された。ただし,修正平均はRコンソールと同じコマンドをスクリプトウィンドウに打って選択し,「Submit」ボタンをクリックしなくては計算できない。単純な平均値は東日本が10.5,西日本が9.87であるが,乗用車保有台数の影響を調整した修正平均は,東日本が9.44,西日本が11.0と逆転し,かつ有意水準5%で統計学的な有意差があるといえた。
EZRには共分散分析のメニューがあって,「統計解析」「連続変数の解析」から「連続変数で補正した2群以上の間の平均値の比較(共分散分析ANCOVA)」を選び,「目的変数(1つ選択)」としてTA1989,「Grouping Variables (pick one)」としてREGION,「補正に用いる連続変数(1つ選択)」としてCAR1990を選び,「モデル解析用に解析結果をアクティブモデルとして残す」の左のボックスにチェックを入れて「OK」ボタンをクリックすれば,ほぼ自動的に以上をやってくれる。ただし,修正平均の値だけは自動的には計算されない。保存されたモデルがModel.1という名称だとすると,次のようにR Scriptウィンドウに打ち,選択した上で「実行」ボタンをクリックする(欠損値があった場合を考えると,元データフレームのCAR1990ではなく,このように計算に使われたデータを使う方が良い)。
cfs <- coef(Model.1)
cfs[[1]] + cfs[[3]]*mean(Model.1$model$CAR1990) + c(0, cfs[[2]])ロジスティック回帰分析は,従属変数(目的変数。ロジスティック回帰分析では反応変数,あるいは応答変数と呼ぶこともある)が2値変数であり,二項分布に従うのでlm()ではなく,glm()を使う。
ロジスティック回帰分析の思想としては,例えば疾病の有無を,複数のカテゴリ変数によって表される要因の有無と年齢のような交絡因子によって説明するモデルをデータに当てはめようとする。量的な変数によって表される交絡を調整しながらオッズ比を計算できるのが利点であり,医学統計ではもっともよく使われる手法の一つである。
疾病の有無は0/1で表され,データとしては有病割合(総数のうち疾病有りの人数の割合)となるので,そのままではモデルの左辺は0から1の範囲しかとらないが,右辺は複数のカテゴリ変数と量的変数(多くは交絡因子)からなるので実数のすべての範囲をとる。そのため,左辺をロジット変換(自身を1から引いた値で割って自然対数をとる)する。
つまり,疾病の有病割合をPとすると,ロジスティック回帰モデルは次のように定式化できる。 ln (P/(1 − P)) = b0 + b1X1 + ...bkXk もしX1が要因の有無を示す2値変数で,X2, ...Xkが交絡であるなら,X1 = 0の場合をX1 = 1の場合から引けば, b1 = ln (P1/(1 − P1)) − ln (P0/(1 − P0)) = ln (P1 * (1 − P0)/(P0 * (1 − P1))) となるので,b1が他の変数の影響を調整したオッズ比の対数になる。対数オッズ比が正規分布するとすれば,オッズ比の95%信頼区間が
 として得られる。
として得られる。
例題
library(MASS)のdata(birthwt)は,SpringfieldのBaystate医療センターの189の出生について,低体重出生とそのリスク因子の関連を調べたデータで,次の変数を含んでいる。低体重出生の有無を反応変数としたロジスティック回帰分析をせよ。
データには多くの変数が含まれているが,本来,ロジスティック回帰分析では,反応変数に対する効果を見たい変数と交絡因子となっている変数はすべて説明変数としてモデルに投入するべきである(説明変数と反応変数の両方と有意な相関があれば交絡因子となっている可能性がある)。
ここでは,丁寧な考察を経て,独立変数が人種,喫煙の有無,高血圧既往の有無,子宮神経過敏の有無,最終月経時体重,早期産経験数となったとしよう。ロジスティック回帰分析の前に,数値型で入っているカテゴリ変数を要因型に変換しておく必要がある。Rコンソールでは次のようになる。
library(MASS)
data(birthwt)
birthwt$clow <- factor(birthwt$low, labels=c("NBW", "LBW"))
birthwt$crace <- factor(birthwt$race, labels=c("white", "black", "others"))
birthwt$csmoke <- factor(birthwt$smoke, labels=c("nonsmoke", "smoke"))
birthwt$cht <- factor(birthwt$ht, labels=c("normotensive", "hypertensive"))
birthwt$cui <- factor(birthwt$ui, labels=c("uterine.OK", "uterine.irrit"))
Rcmdrでは,「データ」の「パッケージ内のデータ」の「アタッチされたパッケージからデータセットを読み込む」を選んで開くウィンドウで,パッケージの枠からMASSをダブルクリックし,データセットの枠からbirthwtをダブルクリックした後に,「データ」「アクティブデータセット内の変数の管理」「数値変数を因子に変換」を選び,まず変数としてlowを選び,新しい変数名をclowとして[OK]ボタンをクリックする。数値0が水準1となり(NBWと名付ける),数値1が水準2となる(LBWと名付ける)。次にraceを選び,新変数名をcraceとして[OK]ボタンをクリックし,出てくるウィンドウで第1水準に"white",第2水準に"black",第3水準に"others"とカテゴリ名を指定し,[OK]ボタンをクリックする。smoke,ht,uiについても同様にカテゴリ変数csmoke,cht,cuiに変換する。
EZRでは,「ファイル」「パッケージからデータを読み込む」を選び,パッケージとしてMASSをダブルクリック,次いでデータセットとしてbirthwtをダブルクリックして「OK」ボタンをクリックする。次に「アクティブデータセット」の「変数の操作」から「連続変数を因子に変換する」を選ぶ。あとはRcmdrと同様に操作する。
ロジスティック回帰モデルをこのデータに当てはめるには,Rコンソールでは次のようにする。
res <- glm(clow ~ crace+csmoke+cht+cui+lwt+ptl,
family=binomial(logit), data=birthwt)
summary(res)もしモデルがどの程度データを説明しているのか評価したければ,線型重回帰モデルの自由度調整済み重相関係数の代わりに,NagelkerkeのR2を計算することができる。
require(fmsb)
NagelkerkeR2(res)
Rcmdrでは,「統計量」「モデルへの適合」「一般化線型モデル」で,式の左辺にclow (因子)をクリックして代入し(たんにclowと入る),右辺にcrace+csmoke+cht+cui+lwt+ptlと打つ(またはクリックして選ぶ)。リンク関数族をbinomialにして,リンク関数をlogitにして[OK]する。RcmdrではNagelkerkeのR2を求めるオプションはない。
EZRでは,「統計解析」「名義変数の解析」「二値変数に対する多変量解析(ロジスティック回帰)」を選ぶ。まず「目的変数」の枠をアクティブにしてからclow [因子]をダブルクリックすると「目的変数」の枠にclowが入る。自動的に「説明変数」の枠がアクティブになるので,そこにcrace+csmoke+cht+cui+lwt+ptlと打つ(または変数をダブルクリック,+の記号ボタンをクリックして選ぶ)。他にもオプションを選べるが,基本的にはこれだけで「OK」ボタンをクリックすればロジスティック回帰分析の結果が得られる。
RコンソールでもRcmdrでも,表示される結果は次の通りである。
Call:
glm(formula = clow ~ crace + csmoke + cht + cui + lwt + ptl,
family = binomial(logit), data = birthwt)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.9049 -0.8124 -0.5241 0.9483 2.1812
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.086550 0.951760 -0.091 0.92754
craceblack 1.325719 0.522243 2.539 0.01113 *
craceothers 0.897078 0.433881 2.068 0.03868 *
csmokesmoke 0.938727 0.398717 2.354 0.01855 *
chthypertensive 1.855042 0.695118 2.669 0.00762 **
cuiuterine.irrit 0.785698 0.456441 1.721 0.08519 .
lwt -0.015905 0.006855 -2.320 0.02033 *
ptl 0.503215 0.341231 1.475 0.14029
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 234.67 on 188 degrees of freedom
Residual deviance: 201.99 on 181 degrees of freedom
AIC: 217.99
Number of Fisher Scoring iterations: 4この出力からロジスティック回帰分析の結果は,下表のようにまとめられる。このように,量的な変数は表の下に共変量として調整したと書くのが普通である。また,係数は対数オッズ比でなく指数をとってオッズ比に直し,95%信頼区間も表示する。この操作は残念ながらRcmdrではまだできないので,分析結果が付値されている変数(回帰分析のモデルを指定するウィンドウの中で「モデル名」として指定したもの)がGLM.1だったとすると,Rコンソールで,exp(coef(GLM.1))とすればオッズ比の点推定量が得られるし,exp(confint(GLM.1))とすれば95%信頼区間が得られる。
EZRでは,上の出力の後に,各変数についてのオッズ比と95%信頼区間,p値も自動的に表示される。NagelkerkeのR2は出力に含まれていないので,必要な場合はfmsbパッケージをロードし,NagelkerkeR2()関数にアクティブモデル名を与える。
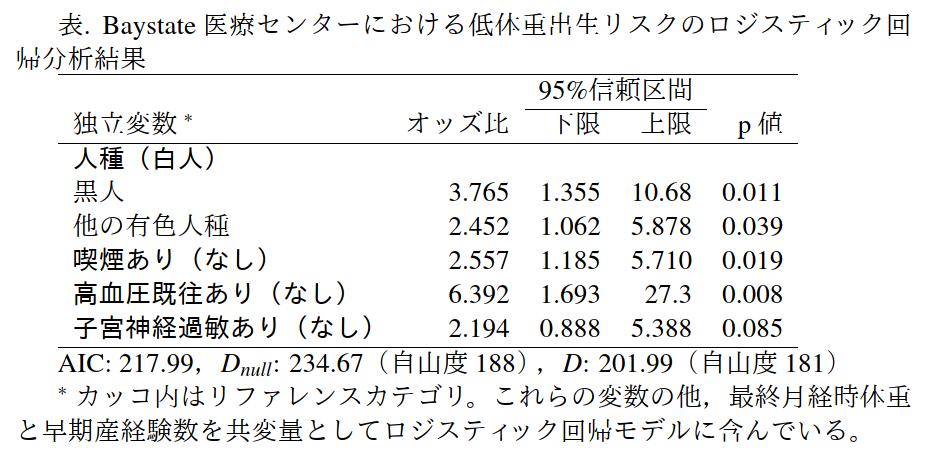
New England Journal of Medicine誌の統計報告ガイドラインのセクションB項目gに「In general, relative risk estimates are the preferred quantities to report. If authors plan to rely on odds ratios in the analysis, a justification should be provided in the Methods section addressing the concerns that odds ratios may overestimate the relative risks and may be misinterpreted.」とあるように、有病割合が高いときのオッズ比が過大評価になることは問題視されている。
統計数理研究所の野間久史による「修正ポアソン回帰・修正最小二乗回帰による2値アウトカムデータの多変量解析」が大変わかりやすいが、係数が求められるならば、glm()関数のfamily=オプションでbinomial(link="logit")として対数オッズ比を推定するよりも、family=binomial(link="log")として対数リスク比を推定したり、family=binomial(link="identity")としてリスク差を推定する方が良いが、多くの場合収束しない。そこで、rqlmパッケージのrqlm()関数を使い、family=poisson, eform=TRUEというオプションを付けて修正ポアソン回帰分析を実行することでバイアスのないリスク比の推定値を95%信頼区間付きで推定するか、同じrqlm()関数でfamily=gaussianとして修正最小二乗回帰分析を行い、バイアスのないリスク差を推定することが薦められている。
ポアソン回帰分析は,ロジスティック回帰分析では二項分布に従う2値変数だった応答変数が,ポアソン分布に従う整数(計数値)である場合に当てはめるモデルである94。ロジスティック回帰分析と同じくglm()を使い,リンク関数を変えるだけで実行可能である。EZRではRcmdrのオリジナルメニューである「標準メニュー」の「統計量」の「モデルへの適合」の「一般化線型モデル」を選び,familyとしてpoissonをダブルクリックし,リンク関数として適切なもの(デフォルトはlog)を選べばよい。
farawayパッケージに含まれているgalaというデータフレームは,Johnson and Raven (1973)とWeisberg (2005)で提示されているデータで95,ガラパゴス諸島の30の島のそれぞれの植物の種数96(変数名Species)とその島の固有種の数(Endemics)に加えて,島の面積(km2単位,Area),最高地点の標高(m単位,Elevation),最寄りの島までの距離(km単位,Nearest),サンタクルス島までの距離(km単位,Scruz),隣接する島の面積(km2単位,Adjacent)という5つの地理的変数を含んでいる。
Faraway (2006)は,このデータを使って,カメの種の数を,地理的変数でポアソン回帰する例を示している。Faraway (2006)に示されている通り97,実は種数の平方根を従属変数にした線形重回帰でも自由度調整済み重相関係数の2乗が0.737あり,それほど適合は悪くないが,平方根変換の意味づけが難しいし,元々何種かあった(それが切片となるはず)植物がそれぞれの島で独立に種分化したとしたら,種数はポアソン分布に従うだろうと考えるのは合理的な仮定であろう。ポアソン回帰のコードは以下のようになる。
if (require(faraway)==FALSE) {
install.packages("faraway", dep=TRUE)
library(faraway)
}
data(gala)
gala <- gala[, -2] # delete the number of endemic species column
res <- glm(Species ~., data=gala, family=poisson) # Poisson regression
summary(res)実行すると,次の枠内の結果が得られる。
Call:
glm(formula = Species ~ ., family = poisson, data = gala)
Deviance Residuals:
Min 1Q Median 3Q Max
-8.2752 -4.4966 -0.9443 1.9168 10.1849
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 3.155e+00 5.175e-02 60.963 < 2e-16 ***
Area -5.799e-04 2.627e-05 -22.074 < 2e-16 ***
Elevation 3.541e-03 8.741e-05 40.507 < 2e-16 ***
Nearest 8.826e-03 1.821e-03 4.846 1.26e-06 ***
Scruz -5.709e-03 6.256e-04 -9.126 < 2e-16 ***
Adjacent -6.630e-04 2.933e-05 -22.608 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for poisson family taken to be 1)
Null deviance: 3510.73 on 29 degrees of freedom
Residual deviance: 716.85 on 24 degrees of freedom
AIC: 889.68
Number of Fisher Scoring iterations: 5結果を見るとAICが約890と大きく,Residual devianceの値から,p値として,1-pchisq(717, df=24)を計算させるとほぼゼロとなって当てはまりが良くないことがわかる。通常,こういうときは外れ値の影響を疑うものだが,残差を半正規確率プロット(half-normal plot)させてみると,とくに大きな外れ値はなさそうである。また,このモデルによって説明されるデータのばらつきは,1-3511/717を計算すると0.796となり,種数を平方根変換したときの線形重回帰と大差ない。
しかし,もし本当に応答変数である植物の種数がポアソン分布に従っているなら,ポアソン分布は平均と分散が等しいはずなので,このモデルによる予測値(平均値)を横軸に98,分散の近似値として残差の二乗を縦軸に99とって散布図を描いてみたら確認できるはずである。実行して得られるグラフから,平均と分散には正の相関関係はあるけれども,分散の方が大きな値をとることがわかる。応答変数がポアソン分布に従うというポアソン回帰の仮定が崩れているけれども,リンク関数と独立変数群の選択が間違っていないとしたら,各独立変数の係数は(結果の中でEstimateとなっているカラム)正しいが,標準誤差が間違った値になる。そうなると,どの独立変数が統計的に有意なのかということが,上記の結果からは決定できないことになってしまう。
halfnorm(residuals(res))
plot(log(fitted(res)), log((gala$Species-fitted(res))^2),
xlab=expression(hat(mu)), ylab=expression((y-hat(mu))^2))この過拡散(overdispersion)という問題を解決するためのアプローチの1つとしては,ポアソン過程で発生する応答がそれ自体ガンマ分布に従う確率変数λで起こるとしてしまう手がある。λの期待値がポアソン分布の期待値μと同じ,分散がμ/ϕであると仮定することで,応答変数は負の二項分布に従うようになり,平均はポアソン分布と同じでμ,分散はμ(1 + ϕ)/ϕとなる。拡散パラメータϕの推定値は次の枠内のようにすればdpとして得られ,それを使ってsummary()を取り直せば標準誤差が正しく推定できる。ただし,この場合には正規分布を使った検定は信頼性が低いので,F検定を使うべきである(とFaraway (2006)は書いている)。
dp <- sum(residuals(res, type="pearson")^2 / res$df.res)
print(dp)
summary(res, dispersion=dp)
drop1(res, test="F")こうして得られた結果から,島の面積,最高地点の標高,隣接する島の面積の3つの変数がガラパゴス諸島の島ごとの植物種数を有意に説明しているといえた。表としては,以下のようにまとめられる。

多項ロジスティック回帰分析は,ロジスティック回帰分析の拡張である。通常のロジスティック回帰分析では応答変数が二項分布に従う2値変数だったが,多項ロジスティック回帰分析では多項分布に従う3水準以上のカテゴリ変数である。glm()ではなく,追加パッケージを使うのが普通である。EZRのメニュー上では「標準メニュー」として残っているRcmdrのオリジナルメニューの,「統計量」の「モデルへの適合」の「多項ロジットモデル」を使って実行可能である(なお,このメニューで使われている関数は,後述するnnetパッケージのmultinom()関数である)。モデルの当てはめ後に変数選択するとか,係数の信頼区間を求めるなどの手続きも,「標準メニュー」の「モデル」から可能である。
Faraway (2006)のChapter 5でもnnetパッケージのmultinom()関数を使う方法が解説されているが,ドイツのクリスティアン・アルブレヒト大学キールの心理学教室のサイトにある多項ロジスティック回帰分析のパッケージを比較した記事100を読む限りでは,nnetパッケージのmultinom()関数,mlogitパッケージのmlogit()関数101,VGAMパッケージのvglm()関数の中では,vglm()関数が多機能であるように思われた。また,RPubsに掲載されている多項ロジスティック回帰分析の記事(http://rpubs.com/kaz_yos/VGAM)が,VGAMパッケージのvglm()関数の使い方をわかりやすく説明してくれているので,これを参考にするとよいと思う。また,カリフォルニア大学ロサンゼルス校の記事102も参考になる。効果のビジュアル化については,John Foxによるhttps://core.ac.uk/download/pdf/6287961.pdfがわかりやすい。
Faraway (2006)のChapter 5の例を挙げておく。同書に含まれている関数やデータはfarawayというパッケージをインストールして呼び出せば使えるようになる。Faraway (2006)には同じ1996年の米国選挙における支持政党のデータを使って,民主党,どちらでもない,共和党をただのカテゴリと扱う場合と,順序付きカテゴリとして扱う場合のやり方が書かれているが,本稿では前者のみ示す。
なお,欠損値や「わからない」と答えた人や,ビル・クリントンとボブ・ドール以外の支持者はデータから予め除き,結果として944人についての10個の変数が含まれている。
変数は以下の通りで,元々水準が多い順序付き要因型変数であるPIDやincomeをそのまま分析すると結果が解釈しにくいので,PIDは3水準に再カテゴリ化した変数sPIDを作成し,incomeは所得の幅のほぼ中央値をとって数値化した変数nincomeを作成して分析する。
多項ロジスティック回帰分析をするコードは以下の通りである。
if (require(faraway)==FALSE) {
install.packages("faraway", dep=TRUE)
library(faraway)
}
library(nnet)
data(nes96)
sPID <- nes96$PID
levels(sPID) <- c("Democrat","Democrat","Independent","Independent",
"Independent","Republic","Republic") # reduce levels from 7 to 3
inca <- c(1.5, 0:2*2+4, 9:14+0.5, 0:3*2.5+16, 0:4*5+27.5, 55, 67.5, 82.5, 97.5, 115)
nincome <- inca[unclass(nes96$income)] # conv ordered factor to numeric
res <- multinom(sPID ~ age + educ + nincome, data=nes96)
summary(res)下枠内の結果が得られる。
Call:
multinom(formula = sPID ~ age + educ + nincome, data = nes96)
Coefficients:
(Intercept) age educ.L educ.Q educ.C
Independent -1.197260 0.0001534525 0.06351451 -0.1217038 0.1119542
Republic -1.642656 0.0081943691 1.19413345 -1.2292869 0.1544575
educ^4 educ^5 educ^6 nincome
Independent -0.07657336 0.1360851 0.15427826 0.01623911
Republic -0.02827297 -0.1221176 -0.03741389 0.01724679
Std. Errors:
(Intercept) age educ.L educ.Q educ.C educ^4
Independent 0.3265951 0.005374592 0.4571884 0.4142859 0.3498491 0.2883031
Republic 0.3312877 0.004902668 0.6502670 0.6041924 0.4866432 0.3605620
educ^5 educ^6 nincome
Independent 0.2494706 0.2171578 0.003108585
Republic 0.2696036 0.2031859 0.002881745
Residual Deviance: 1968.333
AIC: 2004.333 同じデータをVGAMパッケージのvglm()関数で分析するコードは以下の通り。
library(VGAM) # to use vglm()
res <- vglm(sPID ~ age + educ + nincome, data=nes96, family=multinomial)
summary(res)下枠内の結果が得られる。Faraway (2006)には各係数についてカイ二乗検定する方法が書かれているが,vglm()関数ではp値も自動的に表示される。応答変数のリファレンスカテゴリは3番目の水準と書かれているので,これらの係数は共和党支持よりも民主党支持(1)かどちらでもない(2)へのなりやすさを示す。ageやnincomeは係数が負なので,年齢や所得が高いほど共和党支持になりやすいことを意味する(年齢は5%水準で有意でないが)。応答変数のリファレンスカテゴリが違うだけで,結果としてはnnetパッケージを使った場合と同様である。
Call:
vglm(formula = sPID ~ age + educ + nincome, family = multinomial,
data = nes96)
Pearson residuals:
Min 1Q Median 3Q Max
log(mu[,1]/mu[,3]) -2.986 -0.8454 -0.3919 1.000 2.267
log(mu[,2]/mu[,3]) -2.318 -0.7826 -0.2850 1.198 2.283
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept):1 1.642650 0.331255 4.959 7.09e-07 ***
(Intercept):2 0.445389 0.372285 1.196 0.2316
age:1 -0.008194 0.004903 -1.671 0.0946 .
age:2 -0.008041 0.005619 -1.431 0.1524
educ.L:1 -1.194114 0.650009 -1.837 0.0662 .
educ.L:2 -1.130593 0.713072 -1.586 0.1128
educ.Q:1 1.229265 0.603936 2.035 0.0418 *
educ.Q:2 1.107555 0.660372 1.677 0.0935 .
educ.C:1 -0.154448 0.486465 -0.317 0.7509
educ.C:2 -0.042485 0.531864 -0.080 0.9363
educ^4:1 0.028269 0.360477 0.078 0.9375
educ^4:2 -0.048311 0.397628 -0.121 0.9033
educ^5:1 0.122118 0.269581 0.453 0.6506
educ^5:2 0.258208 0.296246 0.872 0.3834
educ^6:1 0.037413 0.203183 0.184 0.8539
educ^6:2 0.191694 0.226809 0.845 0.3980
nincome:1 -0.017247 0.002882 -5.985 2.17e-09 ***
nincome:2 -0.001008 0.002917 -0.345 0.7297
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Names of linear predictors: log(mu[,1]/mu[,3]), log(mu[,2]/mu[,3])
Residual deviance: 1968.332 on 1870 degrees of freedom
Log-likelihood: -984.1663 on 1870 degrees of freedom
Number of Fisher scoring iterations: 4
No Hauck-Donner effect found in any of the estimates
Reference group is level 3 of the response次にMASSパッケージに含まれているminn38というデータを使って説明する。このデータは,1938年のミネソタ州における高校の卒業生の進路についての集計値である。変数は以下の通り。
高校卒業後の進路が性別,高校のランク,父親の職業水準によって説明されるというモデルを当てはめるには,下のコードを打てば良い。
library(MASS)
minn38$hs <- as.ordered(minn38$hs)
minn38$fol <- as.ordered(minn38$fol)
res <- multinom(phs ~ hs + fol + sex, weights=f, data=minn38)
summary(res)得られる結果は下枠内の通りである。
Call:
multinom(formula = phs ~ hs + fol + sex, data = minn38, weights = f)
Coefficients:
(Intercept) hs.L hs.Q fol.L fol.Q fol.C fol^4
E -0.6546827 -0.2624524 -0.04730188 0.8747934 -0.7402795 0.4002617 -0.4295513
N -1.2038733 -0.4176488 -0.12268126 0.7545555 -0.6906311 0.5286980 -0.3284744
O 0.9958172 -1.1253635 -0.08545117 1.5057952 -0.6788387 0.4125037 -0.5293829
fol^5 fol^6 sexM
E -0.5471209 0.46682830 -0.9904394
N -0.2194172 0.04308761 -1.3272296
O -0.6055241 0.41878445 -0.2059234
Std. Errors:
(Intercept) hs.L hs.Q fol.L fol.Q fol.C fol^4
E 0.05077846 0.06746142 0.05795464 0.12210938 0.1127652 0.11361974 0.10893022
N 0.06306977 0.08679242 0.07356078 0.15800767 0.1446081 0.14894973 0.14095890
O 0.03463955 0.04207937 0.03619215 0.07511298 0.0682409 0.07199713 0.07019344
fol^5 fol^6 sexM
E 0.10451289 0.08968776 0.07255349
N 0.13940822 0.11562495 0.10183668
O 0.06869718 0.05738971 0.04328839
Residual Deviance: 26546.35
AIC: 26606.35 同じデータをVGAMパッケージのvglm()関数で分析するには,下のコードを打つ(上に示した順序付き要因型への変換を済ませた後で実行する)。
library(VGAM) # to use vglm()
res <- vglm(phs ~ hs + fol + sex, weights=f, data=minn38, family=multinomial)
summary(res)下枠内の結果が得られる。
Call:
vglm(formula = phs ~ hs + fol + sex, family = multinomial, data = minn38, weights = f)
Pearson residuals:
Min 1Q Median 3Q Max
log(mu[,1]/mu[,4]) -16.19 -4.109 -1.3042 1.285 33.33
log(mu[,2]/mu[,4]) -13.44 -2.489 -0.7190 1.651 33.00
log(mu[,3]/mu[,4]) -8.86 -1.615 -0.4686 1.161 33.33
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept):1 -0.99583 0.03464 -28.749 < 2e-16 ***
(Intercept):2 -1.65049 0.04489 -36.767 < 2e-16 ***
(Intercept):3 -2.19976 0.05841 -37.659 < 2e-16 ***
hs.L:1 1.12539 0.04208 26.745 < 2e-16 ***
hs.L:2 0.86296 0.06065 14.229 < 2e-16 ***
hs.L:3 0.70800 0.08186 8.649 < 2e-16 ***
hs.Q:1 0.08544 0.03619 2.361 0.018241 *
hs.Q:2 0.03818 0.05237 0.729 0.466038
hs.Q:3 -0.03738 0.06951 -0.538 0.590800
fol.L:1 -1.50581 0.07511 -20.047 < 2e-16 ***
fol.L:2 -0.63088 0.11306 -5.580 2.41e-08 ***
fol.L:3 -0.75116 0.15079 -4.982 6.31e-07 ***
fol.Q:1 0.67889 0.06824 9.949 < 2e-16 ***
fol.Q:2 -0.06142 0.10595 -0.580 0.562109
fol.Q:3 -0.01176 0.13904 -0.085 0.932570
fol.C:1 -0.41241 0.07200 -5.728 1.02e-08 ***
fol.C:2 -0.01218 0.10345 -0.118 0.906266
fol.C:3 0.11633 0.14101 0.825 0.409380
fol^4:1 0.52943 0.07019 7.542 4.61e-14 ***
fol^4:2 0.09981 0.09757 1.023 0.306298
fol^4:3 0.20084 0.13206 1.521 0.128294
fol^5:1 0.60551 0.06870 8.814 < 2e-16 ***
fol^5:2 0.05839 0.09298 0.628 0.530044
fol^5:3 0.38604 0.13067 2.954 0.003133 **
fol^6:1 -0.41882 0.05739 -7.298 2.93e-13 ***
fol^6:2 0.04804 0.08210 0.585 0.558451
fol^6:3 -0.37580 0.10956 -3.430 0.000604 ***
sexM:1 0.20593 0.04329 4.757 1.96e-06 ***
sexM:2 -0.78456 0.06805 -11.530 < 2e-16 ***
sexM:3 -1.12139 0.09880 -11.350 < 2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Names of linear predictors: log(mu[,1]/mu[,4]), log(mu[,2]/mu[,4]), log(mu[,3]/mu[,4])
Residual deviance: 26546.35 on 474 degrees of freedom
Log-likelihood: -13273.17 on 474 degrees of freedom
Number of Fisher scoring iterations: 5
No Hauck-Donner effect found in any of the estimates
Reference group is level 4 of the response結果の最下行に書かれている通り,リファレンスグループが応答変数の第4水準ということなので,例えば,sexM:1の係数が0.20593と正であることは,進路「その他」に比べて男性は大学進学しやすいということを意味すると解釈される。
順序のある多項ロジスティック回帰分析をしたい場合は,MASSパッケージのpolr()関数を使えば,比例オッズモデルを当てはめることができる。詳細は藤井(2010)のpp.98-100を参照されたいが,簡単に使い方だけ紹介しておく。MASSパッケージに含まれているhousingというデータフレームを使って説明されている。このデータフレームはデンマーク建造物研究所とデンマークメンタルヘルス研究所によって共同で実施された住宅調査の結果である。調査参加者はコペンハーゲンの12の地区の住民である。建物はすべて1960年から1968年の間に建てられたもので,12の地区は住民の社会的水準ができるだけばらつかないように選ばれた。各地区から1~6のセクションを選び,各セクションから約50人の住民を対象に調査した。含まれている変数は以下の通りである。
満足度が他の住民との接触の程度によって説明されるというモデルを考える。比例オッズモデルでは,満足度中と満足度高の合計に対する満足度低の比の対数が,他の住民との接触の程度の違いによって説明されるという線型モデルの係数が,満足度高に対する満足度中と満足度低の合計の比の対数が,他の住民との接触の程度の違いによって説明されるという線型モデルの係数と共通であると仮定して,係数を推定する。
library(MASS)
res <- polr(Sat ~ Cont, weight=Freq, data=housing)
summary(res)上枠内のコードを実行すると,下枠内の結果が得られる。
Call:
polr(formula = Sat ~ Cont, data = housing, weights = Freq)
Coefficients:
Value Std. Error t value
ContHigh 0.1651 0.09131 1.808
Intercepts:
Value Std. Error t value
Low|Medium -0.5804 0.0735 -7.8980
Medium|High 0.5131 0.0732 7.0119
Residual Deviance: 3645.608
AIC: 3651.608 ContHighの係数が0.165で正なので,他の住民との接触が多いと感じている方が住居への満足度が高くなることがわかる(但し統計的に5%有意ではない,と藤井(2010)に書かれている。p値の求め方は書かれていないが,t値が1.808で,サンプルサイズが1651なので,自由度1649と考えたらp値は0.07程度であろうと思われる)。
同じデータをVGAMパッケージのvglm()関数で分析するコードは以下の通り。
library(MASS) # to load housing data
library(VGAM) # to use vglm function
res <- vglm(Sat ~ Cont, weights=Freq, data=housing, family=propodds)
summary(res)で,実行すると下枠内の結果が得られる。これにはp値も示されていて,確かに0.07程度のようである。比例係数の指数をとった値も最後に示されていて,他の住民との接触が多いと満足度が1.18倍になると解釈される。
Call:
vglm(formula = Sat ~ Cont, family = propodds, data = housing,
weights = Freq)
Pearson residuals:
Min 1Q Median 3Q Max
logitlink(P[Y>=2]) -12.248 -3.759 1.740 3.451 7.511
logitlink(P[Y>=3]) -8.463 -3.613 -1.689 4.078 10.486
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept):1 0.58042 0.07305 7.946 1.93e-15 ***
(Intercept):2 -0.51307 0.07273 -7.055 1.73e-12 ***
ContHigh 0.16507 0.09114 1.811 0.0701 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Names of linear predictors: logitlink(P[Y>=2]), logitlink(P[Y>=3])
Residual deviance: 3645.608 on 141 degrees of freedom
Log-likelihood: -1822.804 on 141 degrees of freedom
Number of Fisher scoring iterations: 3
No Hauck-Donner effect found in any of the estimates
Exponentiated coefficients:
ContHigh
1.179476 3つ以上のグループの間で比較をするとき,それらが互いに独立で,位置母数を比較するためなら,一元配置分散分析またはクラスカル=ウォリスの検定を行うことは,既に示した。
それに対して,同じ対象者について3つ以上の測定値がある場合の,測定値間での比較は? というのが,この節での主題となる反復測定分散分析またはフリードマンの検定である。手作業でやるのは大変だが,EZRでは簡単に実行できる103。ただし,注意しなければならない点が2つある。
第一に,データが横長形式になっている必要がある(異なる時点の測定値は異なる変数とする。1行が1人を表す)ということである。
第二に,時間に依存する変数の名前をアルファベット順に与える必要がある(T2とT10ではT10が先と判定されるので,T02などと0を入れなくてはいけない)ということである。そうなっていない場合は,「アクティブデータセット」「変数の操作」「変数名を変更する」で名前を変える。
以上2点さえ注意すれば手順は簡単である。
大雑把に言えば,データ読み込み→グラフを描く→統計解析という流れになる。統計解析の内容は以下3つである。
EZRでの手順を示す。
calmness,despair,fear,happinessの4つを選ぶ(複数選ぶ時はキーボードのを押しながらクリック)。群別はしないので,そのまま「OK」ボタンをクリックすると,同じ人を線で結んだ,心理的刺激に対する皮膚電位ポテンシャルのグラフが表示される。個人差が大きく,どの心理刺激でも高い電位を示しがちな人が2人いることがわかるcalmness despair fear happiness
18.20 18.70 22.05 21.15
Friedman chi-squared = 6.45, df = 3, p-value = 0.09166データの出典は,B.エヴェリット(著),石田基宏他(訳)(2007)『RとS-PLUSによる多変量解析』シュプリンガー・ジャパンの第9章である。
T.0,T.0.5,…,T.5を選び(連続する複数の変数を選ぶには,まず1番上の変数のところでクリックし,キーを押しながら一番下の変数のところでクリックする),群別変数としてGROUPを選んでから「OK」ボタンをクリックする

GROUPは2つのカテゴリからなる因子型の変数で,“Control”が対照,“Obesity”が肥満である。T.0,T.0.5,…,T.5を選び,群別変数としてGROUPを選んで「OK」ボタンをクリックすると以下の結果が得られる。Univariate Type III Repeated-Measures ANOVA Assuming Sphericity
Sum Sq num Df Error SS den Df F value Pr(>F)
(Intercept) 3356.2 1 71.407 31 1457.0243 < 2.2e-16 ***
Factor1.GROUP 15.3 1 71.407 31 6.6592 0.01482 *
Time 39.2 7 38.098 217 31.9359 < 2.2e-16 ***
Factor1.GROUP:Time 7.7 7 38.098 217 6.2887 0.0000009947 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Mauchly Tests for Sphericity
Test statistic p-value
Time 0.051567 0.000000098002
Factor1.GROUP:Time 0.051567 0.000000098002
Greenhouse-Geisser and Huynh-Feldt Corrections
for Departure from Sphericity
GG eps Pr(>F[GG])
Time 0.55044 < 2.2e-16 ***
Factor1.GROUP:Time 0.55044 0.0001546 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
HF eps Pr(>F[HF])
Time 0.6383131 3.752241e-20
Factor1.GROUP:Time 0.6383131 5.710639e-05そもそも群の効果がp=0.015で有意だが,球面性検定の結果が時間の効果についても交互作用効果についても有意なので,これらについてはG-GまたはH-F補正後の数値を見て,どちらも5%水準で有意であることがわかる。このデータについても,ノンパラメトリックなフリードマンの検定をすることも可能である。
EZRは内部的にこの処理をcarパッケージのAnova()関数を使って行っている。EZRを使わずに実行するためのコードは以下の通り。
ogtt <- read.delim("https://minato.sip21c.org/ogtt02.txt")
times <- c(0, 0.5, 1, 1.5, 2:5)
control <- subset(ogtt, GROUP=="Control")
obesity <- subset(ogtt, GROUP=="Obesity")
layout(t(1:2))
matplot(times, t(control[, 3:10]), type="l", col=1, lty=1, ylim=c(1, 7),
main="control", xlab="hours after ogtt", ylab="plasma phosphate")
matplot(times, t(obesity[, 3:10]), type="l", col=1, lty=1, ylim=c(1, 7),
main="obesity", xlab="hours after ogtt", ylab="plasma phosphate")
library(car)
contrasts(ogtt$GROUP) <- "contr.sum" # To calculate type3 SS correctly
rma <- lm(cbind(T.0, T.0.5, T.1, T.1.5, T.2, T.3, T.4, T.5) ~ GROUP,
data=ogtt)
summary(rma)
inhour <- ordered(times)
idata <- data.frame(inhour)
res.anova <- Anova(rma, idata=idata, idesign=~inhour, type=3)
summary(res.anova, multivariate=FALSE) # Slightly different from EZRエヴェリット(2007)に掲載されているように,対照群と肥満群のグラフを別々に描くと以下のようになる(EZRでもオプション指定で可能である。ただしEZRは散布図でなく折れ線グラフなので間隔が30分でも1時間でも同じ幅でプロットされている)。
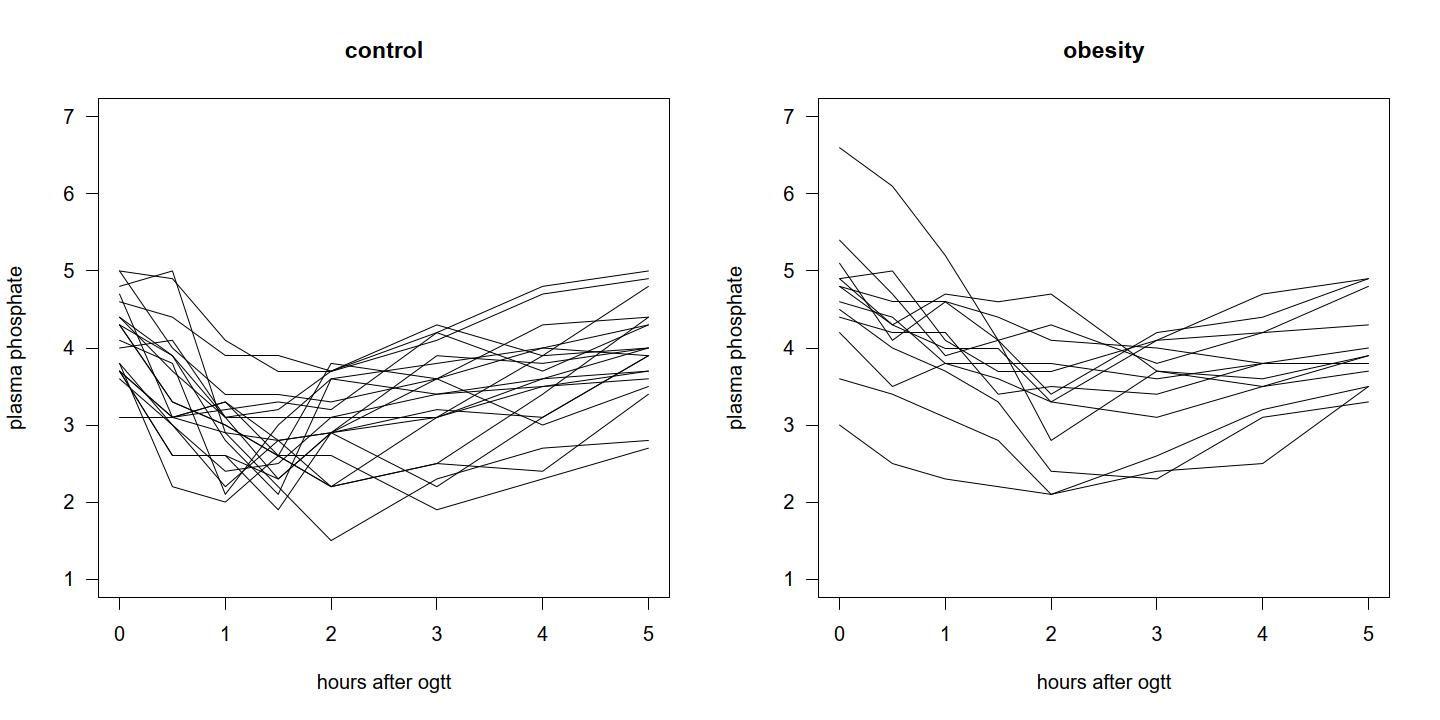
表示される解析結果は,おそらくoptions()のdigits=かscipen=の指定が違うせいで浮動小数点表示方法に違いがあるものの,基本的に同じものである。
Univariate Type III Repeated-Measures ANOVA Assuming Sphericity
Sum Sq num Df Error SS den Df F value Pr(>F)
(Intercept) 3356.2 1 71.407 31 1457.0243 < 2.2e-16 ***
GROUP 15.3 1 71.407 31 6.6592 0.01482 *
inhour 39.2 7 38.098 217 31.9359 < 2.2e-16 ***
GROUP:inhour 7.7 7 38.098 217 6.2887 9.947e-07 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Mauchly Tests for Sphericity
Test statistic p-value
inhour 0.051567 9.8002e-08
GROUP:inhour 0.051567 9.8002e-08
Greenhouse-Geisser and Huynh-Feldt Corrections
for Departure from Sphericity
GG eps Pr(>F[GG])
inhour 0.55044 < 2.2e-16 ***
GROUP:inhour 0.55044 0.0001546 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
HF eps Pr(>F[HF])
inhour 0.6383131 3.752241e-20
GROUP:inhour 0.6383131 5.710639e-05エヴェリット(2007)は,この解析をcarパッケージのAnova()ではなく,混合効果モデルを使って実行するため,nlmeパッケージのlme()関数を用いる方法を紹介している。個人をグループ変数と考えれば,個人差を切片の差,あるいは傾きと切片の両方の違いという形で混合効果モデルに吸収させることが可能である。現在では混合効果モデルならばlmerTestパッケージのlmer()関数を使うのが便利である。ただし混合効果モデルを当てはめるには,まずデータを縦長形式に変換する必要があることに注意が必要である。縦長形式への変換にはreshape()関数を使うと便利である(ただし,おそらく最近はtidyverse系の機能を使う方が普通であろう)。コードと結果を以下に示す。
# Reading data from internet
ogtt <- read.delim("https://minato.sip21c.org/ogtt02.txt")
# define times when data were obtained
times <- c(0:3*0.5, 2:5)
ogttlong <- reshape(ogtt, varying=sprintf("T.%g", times), v.names="pp",
timevar="hours", idvar="ID", direction="long")
ogttlong$hours <- times[ogttlong$hours]
# usual linear regression, with times-squared as an independent variable
resind <- lm(pp ~ hours + I(hours*hours) + GROUP, data=ogttlong)
summary(resind)
# mixed model
library(lmerTest)
reslme0A <- lmer(pp ~ hours + GROUP + (1|ID),
data=ogttlong, REML=FALSE)
reslme0B <- lmer(pp ~ hours + GROUP + hours:GROUP + (1|ID),
data=ogttlong, REML=FALSE)
summary(reslme0A)
summary(reslme0B)
anova(reslme0A, reslme0B)
reslme1 <- lmer(pp ~ hours + I(hours*hours) + GROUP + (1|ID),
data=ogttlong, REML=FALSE)
reslme2 <- lmer(pp ~ hours + I(hours*hours) + GROUP + hours:GROUP + (1|ID),
data=ogttlong, REML=FALSE)
summary(reslme1)
summary(reslme2)
anova(reslme1, reslme2)
reslme3 <- lmer(pp ~ hours + I(hours*hours) + GROUP + (hours|ID),
data=ogttlong, REML=FALSE)
reslme4 <- lmer(pp ~ hours + I(hours*hours) + GROUP + hours:GROUP + (hours|ID),
data=ogttlong, REML=FALSE)
summary(reslme3)
summary(reslme4)
anova(reslme3, reslme4)まず時刻の二乗を独立変数として含む線形重回帰分析の結果は以下の通りである(この結果はエヴェリット(2007)の表9.8と一致するはずだが,なぜか微妙に異なる)。個人差を無視しても,時刻,時刻の二乗,グループのすべてが血漿無機リン酸濃度に影響していると言える。なお,グラフから明らかにわかる通り,経時変化が単調でないため,二乗の項を入れないと時刻の効果も有意でなくなる。
Call:
lm(formula = pp ~ hours + I(hours * hours) + GROUP, data = ogttlong)
Residuals:
Min 1Q Median 3Q Max
-1.61076 -0.51352 0.02139 0.47504 2.11457
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.99211 0.09921 40.237 < 2e-16 ***
hours -0.83115 0.09520 -8.730 3.14e-16 ***
I(hours * hours) 0.16361 0.01842 8.881 < 2e-16 ***
GROUPObesity 0.49332 0.08647 5.705 3.16e-08 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.6865 on 260 degrees of freedom
Multiple R-squared: 0.3008, Adjusted R-squared: 0.2928
F-statistic: 37.29 on 3 and 260 DF, p-value: < 2.2e-16混合効果モデルの結果は以下の通りである。まずランダム切片モデルで見てみる。
> summary(reslme0A)
Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
method [lmerModLmerTest]
Formula: pp ~ hours + GROUP + (1 | ID)
Data: ogttlong
AIC BIC logLik deviance df.resid
562.5 580.4 -276.3 552.5 259
Scaled residuals:
Min 1Q Median 3Q Max
-2.33724 -0.68569 -0.08461 0.73489 2.99361
Random effects:
Groups Name Variance Std.Dev.
ID (Intercept) 0.2227 0.4719
Residual 0.3822 0.6183
Number of obs: 264, groups: ID, 33
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 3.43885 0.12638 45.80778 27.211 <2e-16 ***
hours -0.01740 0.02328 231.00000 -0.748 0.4555
GROUPObesity 0.49332 0.18528 33.00000 2.662 0.0119 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr) hours
hours -0.391
GROUPObesty -0.578 0.000個人差を考えても,時刻の二乗を説明変数に入れないと時刻の効果は有意でない。
> summary(reslme0B)
Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
method [lmerModLmerTest]
Formula: pp ~ hours + GROUP + hours:GROUP + (1 | ID)
Data: ogttlong
AIC BIC logLik deviance df.resid
552.4 573.8 -270.2 540.4 258
Scaled residuals:
Min 1Q Median 3Q Max
-2.33492 -0.63852 -0.06215 0.64658 2.70796
Random effects:
Groups Name Variance Std.Dev.
ID (Intercept) 0.2252 0.4745
Residual 0.3627 0.6022
Number of obs: 264, groups: ID, 33
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 3.30165 0.13174 53.72590 25.062 < 2e-16 ***
hours 0.04716 0.02913 231.00002 1.619 0.106744
GROUPObesity 0.84160 0.20989 53.72590 4.010 0.000189 ***
hours:GROUPObesity -0.16390 0.04640 231.00002 -3.532 0.000498 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr) hours GROUPO
hours -0.470
GROUPObesty -0.628 0.295
hrs:GROUPOb 0.295 -0.628 -0.470時刻とグループ(対照/肥満)の交互作用を考えると,グループの主効果と交互作用効果は有意なので,グループ間で血漿無機リン酸塩濃度に差があり,経時変化パタンもグループによって異なるといえる。これら2つの結果について尤度比検定を行うと,次に示す通り有意な差があるので,交互作用効果を加えた方が有意にあてはまりが良くなると言える。
> anova(reslme0A, reslme0B)
Data: ogttlong
Models:
reslme0A: pp ~ hours + GROUP + (1 | ID)
reslme0B: pp ~ hours + GROUP + hours:GROUP + (1 | ID)
Df AIC BIC logLik deviance Chisq Chi Df Pr(>Chisq)
reslme0A 5 562.51 580.39 -276.26 552.51
reslme0B 6 552.37 573.82 -270.18 540.37 12.149 1 0.0004911 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1次に時刻の二乗を説明変数群に加えてみると,時刻の二乗はもちろんだが,その影響を調整した時刻の効果も有意になる(係数はマイナスなので,時間が経って経口糖負荷の効果が消える部分が二乗の項で説明されると考えれば,この時刻の効果がマイナスなのも納得がいく)。
> summary(reslme1)
Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
method [lmerModLmerTest]
Formula: pp ~ hours + I(hours * hours) + GROUP + (1 | ID)
Data: ogttlong
AIC BIC logLik deviance df.resid
438.3 459.8 -213.1 426.3 258
Scaled residuals:
Min 1Q Median 3Q Max
-2.62326 -0.67286 0.00958 0.54806 2.77540
Random effects:
Groups Name Variance Std.Dev.
ID (Intercept) 0.2428 0.4928
Residual 0.2213 0.4705
Number of obs: 264, groups: ID, 33
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 3.99211 0.12947 50.29035 30.833 <2e-16 ***
hours -0.83115 0.06524 231.00000 -12.739 <2e-16 ***
I(hours * hours) 0.16361 0.01262 231.00000 12.959 <2e-16 ***
GROUPObesity 0.49332 0.18528 33.00000 2.662 0.0119 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr) hours I(*hr)
hours -0.396
I(hors*hrs) 0.330 -0.962
GROUPObesty -0.564 0.000 0.000交互作用を加えても各説明変数の血漿無機リン酸塩濃度への効果はそれほど変化しないが,交互作用効果も有意である。
> summary(reslme2)
Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
method [lmerModLmerTest]
Formula: pp ~ hours + I(hours * hours) + GROUP + hours:GROUP + (1 | ID)
Data: ogttlong
AIC BIC logLik deviance df.resid
418.9 443.9 -202.4 404.9 257
Scaled residuals:
Min 1Q Median 3Q Max
-2.58613 -0.61469 -0.01583 0.61708 3.13886
Random effects:
Groups Name Variance Std.Dev.
ID (Intercept) 0.2453 0.4952
Residual 0.2017 0.4492
Number of obs: 264, groups: ID, 33
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 3.85491 0.13159 53.50053 29.294 < 2e-16 ***
hours -0.76658 0.06376 231.00006 -12.022 < 2e-16 ***
I(hours * hours) 0.16361 0.01205 231.00006 13.574 < 2e-16 ***
GROUPObesity 0.84160 0.19935 44.06226 4.222 0.000119 ***
hours:GROUPObesity -0.16390 0.03461 231.00006 -4.735 3.81e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr) hours I(*hr) GROUPO
hours -0.411
I(hors*hrs) 0.310 -0.940
GROUPObesty -0.597 0.079 0.000
hrs:GROUPOb 0.220 -0.214 0.000 -0.369尤度比検定をすると交互作用を加えたモデルの方が有意に当てはまりが改善しているといえる。
> anova(reslme1, reslme2)
Data: ogttlong
Models:
reslme1: pp ~ hours + I(hours * hours) + GROUP + (1 | ID)
reslme2: pp ~ hours + I(hours * hours) + GROUP + hours:GROUP + (1 | ID)
Df AIC BIC logLik deviance Chisq Chi Df Pr(>Chisq)
reslme1 6 438.29 459.75 -213.15 426.29
reslme2 7 418.89 443.92 -202.45 404.89 21.402 1 3.725e-06 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1最後に切片だけでなく傾きにも個人差があるモデルを当てはめてみる。この結果はエヴェリット(2007)の表9.7と一致するはずだが,やはり微妙に合わない。
> summary(reslme3)
Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
method [lmerModLmerTest]
Formula: pp ~ hours + I(hours * hours) + GROUP + (hours | ID)
Data: ogttlong
AIC BIC logLik deviance df.resid
422.2 450.8 -203.1 406.2 256
Scaled residuals:
Min 1Q Median 3Q Max
-2.85820 -0.57655 -0.01046 0.56493 2.73302
Random effects:
Groups Name Variance Std.Dev. Corr
ID (Intercept) 0.35528 0.5961
hours 0.01523 0.1234 -0.56
Residual 0.17481 0.4181
Number of obs: 264, groups: ID, 33
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 4.01613 0.13881 41.02529 28.933 <2e-16 ***
hours -0.83115 0.06184 227.61654 -13.441 <2e-16 ***
I(hours * hours) 0.16361 0.01122 197.99322 14.582 <2e-16 ***
GROUPObesity 0.43236 0.18448 32.99979 2.344 0.0253 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr) hours I(*hr)
hours -0.453
I(hors*hrs) 0.273 -0.902
GROUPObesty -0.524 0.000 0.000
convergence code: 0
Model failed to converge with max|grad| = 0.00202844 (tol = 0.002, component 1)最終行に示されているように,微妙に収束していないが,この程度なら許容可能であろう。この結果も時刻,時刻の二乗,グループのすべてが血漿無機リン酸塩濃度に有意に影響していることを示している。個人ごとの傾きの推定値は − 0.56であり,固定効果より絶対値が小さいが負の関係が示されている。さらに交互作用効果を見たのが次の結果である。エヴェリット(2007)の表9.9と一致するはずだが微妙にずれている。
> summary(reslme4)
Linear mixed model fit by maximum likelihood . t-tests use Satterthwaite's
method [lmerModLmerTest]
Formula: pp ~ hours + I(hours * hours) + GROUP + hours:GROUP + (hours |
ID)
Data: ogttlong
AIC BIC logLik deviance df.resid
413.6 445.8 -197.8 395.6 255
Scaled residuals:
Min 1Q Median 3Q Max
-2.79396 -0.57037 -0.03002 0.56644 2.88139
Random effects:
Groups Name Variance Std.Dev. Corr
ID (Intercept) 0.315351 0.56156
hours 0.008822 0.09393 -0.48
Residual 0.174800 0.41809
Number of obs: 264, groups: ID, 33
Fixed effects:
Estimate Std. Error df t value Pr(>|t|)
(Intercept) 3.85491 0.14194 38.22608 27.159 < 2e-16 ***
hours -0.76658 0.06296 221.72055 -12.176 < 2e-16 ***
I(hours * hours) 0.16361 0.01122 198.00548 14.582 < 2e-16 ***
GROUPObesity 0.84160 0.21791 32.99104 3.862 0.000497 ***
hours:GROUPObesity -0.16390 0.04645 32.99590 -3.528 0.001254 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Correlation of Fixed Effects:
(Intr) hours I(*hr) GROUPO
hours -0.474
I(hors*hrs) 0.267 -0.886
GROUPObesty -0.605 0.155 0.000
hrs:GROUPOb 0.322 -0.291 0.000 -0.532次に示すように,この場合も,尤度比検定の結果,交互作用効果を含めた方が,有意に当てはまりが良くなっているといえる。
> anova(reslme3, reslme4)
Data: ogttlong
Models:
reslme3: pp ~ hours + I(hours * hours) + GROUP + (hours | ID)
reslme4: pp ~ hours + I(hours * hours) + GROUP + hours:GROUP + (hours |
reslme4: ID)
Df AIC BIC logLik deviance Chisq Chi Df Pr(>Chisq)
reslme3 8 422.21 450.82 -203.11 406.21
reslme4 9 413.65 445.83 -197.82 395.65 10.564 1 0.001153 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1https://minato.sip21c.org/sbp01.txtは,降圧剤投与後の収縮期血圧の変化を示すデータである。有意な経時変化があるかどうかを検討する。
subj T.1 T0 T1 T2 T3 T4 T5 T6 T7 T8
1 112 119 113 105 114 110 115 114 110 111
2 116 110 115 110 112 107 116 115 120 118
3 122 123 126 114 111 113 119 123 119 124
4 124 130 127 110 100 127 130 134 120 124
5 126 121 115 122 124 117 124 132 128 120
6 129 135 125 122 115 110 114 124 133 131まず,これを読み込む。EZRでは,「ファイル」「データのインポート」「ファイル,クリップボード,またはURLからテキストデータを読み込む」を選んで,データセット名をsbp01とし,データファイルの場所をインターネットURLからとし,フィールド区切りをタブとして「OK」ボタンをクリックすると,URL入力画面になるので,URLとして,https://minato.sip21c.org/sbp01.txtと入力する。
次に,変数名T.1をS1に変更する(EZRでは,「アクティブデータセット」「変数の操作」「変数名を変更」で可能)。次に生データの折れ線グラフを描く。「グラフと表」「反復測定データの折れ線グラフ」を選び,出てくるウィンドウで,データを示す変数として,S1, T0, ..., T8を選んでOKすると6本の折れ線グラフが重ね描きされる。
反復測定分散分析は,すべての時点を使うと人数より時点数が多いため解が得られない。敢えてやるなら,時点を絞る必要がある。例えば,「統計解析」「連続変数の解析」「反復測定分散分析」と選び,反復測定データとして,変数T0, T1, ..., T5を指定すれば結果が得られる。
ノンパラメトリックなフリードマンの検定は全データを使っても可能である。「統計解析」「ノンパラメトリック検定」「対応のある3群以上のデータの比較(Friedman検定)」と選び,変数としてS1, T0, ..., T8を選んでOKすると,検定結果としてp=0.029が得られる。従って,降圧剤投与後の時間経過に伴い,収縮期血圧は有意水準5%で統計学的に有意に変化したといえる。
順序変数またはカテゴリ変数について,各個人の同じ変数で2時点での値があるか,あるいは複数の評価者による評価値がある場合,その結果は2次元クロス集計表としてまとめることができ,この表は検査=再検査信頼性,あるいは評価者間信頼性を調べるのに使うことができる。しかし,この目的ではカイ二乗検定もフィッシャーの正確確率も不適切である。なぜなら,各個人の2時点の値や,複数の評価者により同じ人を評価した値は,明らかに独立ではないからである。知りたいのは,偶然の一致とは考えられないほど良く一致しているかどうかといったことになる。
2つの測定値の一致を知りたい場合は,カッパ統計量(κ)を使うことができる。この場合,帰無仮説は,2つの測定値の一致が偶然の一致と同じということであり,対立仮説は,偶然の一致よりも有意に大きい一致になる。
逆に介入効果を知りたい場合など,2時点での測定値があっても,偶然よりも違いがあることを明らかにしたい場合もある。この場合は帰無仮説はカッパ統計量と同じだが,対立仮説が2つの測定値が偶然の一致よりも違っていることになる。この場合はマクネマー(McNemar)の検定が使える。ただし,変数が単なるカテゴリではなく順序変数の場合で,カテゴリ数が3以上なら,ウィルコクソンの符号付き順位検定を使うこともできるし,その方が適切である場合が多い。
検査再検査信頼性を評価するために次の表が得られたとしよう。
| 再検査陽性 | 再検査陰性 | |
|---|---|---|
| 検査結果陽性 | a | b |
| 検査結果陰性 | c | d |
もし2回の検査結果が完璧に一致していたらb = c = 0となるが,通常はb ≠ 0かつ/またはc ≠ 0である。ここで,2回の検査結果の一致確率は,Po = (a + d)/(a + b + c + d)と定義できる。完全な一致の場合,b = c = 0からPo = (a + d)/(a + d) = 1となる。逆に完全な不一致の場合,a = d = 0からPo = 0となる。一致の程度が偶然と同じならば,期待される一致確率Peは,次の式で計算できる。 Pe = {(a + c)(a + b)/(a + b + c + d) + (b + d)(c + d)/(a + b + c + d)}/(a + b + c + d)
ここで,κをκ = (Po − Pe)/(1 − Pe)と定義すると,完全な一致のときκ = 1,偶然と同程度の一致のときκ = 0,偶然の一致より悪い一致のときκ < 0となる。κの分散V(κ)はV(κ) = Pe/{(a + b + c + d) × (1 − Pe)}となるので,κ / √(V(κ))として標準化した統計量は標準正規分布に従う。そこで,κ = 0という帰無仮説を検定したり,κの95%信頼区間を計算することが可能になる。
追加パッケージvcdには,Kappa()という関数があって,κの点推定量を計算できるし,confint()関数を適用すれば95%信頼区間も計算できる。また,筆者もκを計算する関数Kappa.testを開発し公開している。この関数はfmsbパッケージに含まれている。
EZRでは,分割表のすべての組合せの度数がわかっていれば,「統計解析」「検査の正確度の評価」「2つの定性検査の一致度の評価(Kappa係数)」から入力することで,点推定量と95%信頼区間を求めることができるが,Kappa.test()とは異なり一致性の目安は表示されない。
数値計算をしてみよう。次の表を考える。
| 再検査陽性 | 再検査陰性 | |
|---|---|---|
| 検査結果陽性 | 12 | 4 |
| 検査結果陰性 | 2 | 10 |
Rコンソールでは,fmsbパッケージをインストールしてあれば,次の2行を打つだけで,次の枠内に示す結果がすべて得られる。
require(fmsb)
Kappa.test(matrix(c(12,2,4,10),2,2))$Result
Estimate Cohen's kappa statistics and test the null
hypothesis that the extent of agreement is same as random
(kappa=0)
data: matrix(c(12, 2, 4, 10), 2, 2)
Z = 3.0237, p-value = 0.001248
95 percent confidence interval:
0.2674605 0.8753967
sample estimates:
[1] 0.5714286
$Judgement
[1] "Moderate agreement"ここで“Judgement”(一致度の判定)は,下表のLandis JR, Koch GG (1977) Biometrics, 33: 159-174の基準によっている。
| κの値 | 一致度の判定 |
|---|---|
| 負 | "No agreement"(不一致) |
| 0-0.2 | "Slignt agreement"(微かな一致) |
| 0.2-0.4 | "Fair agreement"(多少の一致) |
| 0.4-0.6 | "Moderate agreement"(中程度の一致) |
| 0.6-0.8 | "Substantial agreement"(かなりの一致) |
| 0.8-1.0 | "Almost perfect agreement"(ほぼ完全な一致) |
大雑把なガイドラインに過ぎないが,実用的な基準である。
マクネマーの検定は,元々は2×2クロス集計表について開発された。次の表を考えてみよう。
| 介入後あり | 介入後なし | |
|---|---|---|
| 介入前 あり | a | b |
| 介入前 なし | c | d |
マクネマーの検定では,次のように定義するχ02を計算する。このχ02統計量は,帰無仮説(2回の測定結果の一致の程度が偶然と差が無い)の下で自由度1のカイ二乗分布に従う。 χ02 = {(b-c)2 / (b+c)} 連続性の補正をする場合は次の式になる(ただしbとcが等しいときはχ02 = 0とする)。 χ02 = {(|b-c|-1)2 / (b+c)}
拡張マクネマー検定は,M×Mクロス集計に適用できるようにしたものである(同じ測定を繰り返したときの変化をみるので,必ず行と列のカテゴリ数は一致する)。 セル[i,j] に入る人数をnij(i, j = 1, 2, ..., M)とすると,次の式でχ02を計算することができ,このχ02統計量は帰無仮説([i,j]に入る確率と[j,i]に入る確率が同じ)の下で自由度M(M-1)/2のカイ二乗分布に従う。
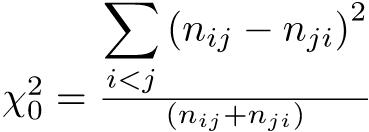
Rコンソールでは,既に関数が提供されていて,対応する2変数間の分割表をTABLEと書くことにすると,マクネマーの検定は,mcnemar.test(TABLE)とするだけでできる。
EZRでは,2×2で度数を直接入力する場合は,前述の方法でκ係数の計算と同時に実行可能である。生データから計算するには,「統計解析」「名義変数の解析」「対応のある比率の比較(二分割表の対称性の検定,McNemar検定)」を選ぶ。
なお,通常の2x2のMcNemarの検定の場合は,N12(1回目はカテゴリ1で2回目はカテゴリ2に変化した人数;以下同様)とN21の両方がゼロだったら2回の間でまったく変化していないということだから,検定する必要がなくなり問題はないが,カテゴリ3つ以上の場合は,例えば,N13はゼロでないがN23とN32がゼロ,という状態だと,(N23+N32)が分母になる項で“Division by zero”エラーがでてしまって,カイ二乗値の計算結果自体がNaNになってしまう。この問題への対処としては,その項をスキップするか(カイ二乗検定をするときにスキップした項数だけ自由度を減らせば良いはず),あるいは全部のセルに極めて小さい数字を足すかすれば計算できるし,実際に"Division by zero"を避けるために全部のセルに0.01を足したと書いてある文献が少なくとも1つは存在する。
共立出版「Rで学ぶデータサイエンス」シリーズの藤井良宜『カテゴリカルデータ解析』には,丁寧に拡張マクネマーの考え方が書かれているけれども分母がゼロの項をどうすべきかについては触れられていないし,「Wonderful R」シリーズの奥村晴彦『Rで楽しむ統計』では,拡張マクネマーについては触れられておらず,そもそも連続量をカットオフで二値化したものならば連続量のままt検定した方が良いという説明がされている。もちろんその通りなのだけれども,最初から3水準以上の名義尺度の変数だと不可能である。カテゴリを併合して2x2にできれば問題解決するが,併合しがたい場合もある。
全部のセルに0.01を足すのは,検定したい行列オブジェクトをxとして,mcnemar.test(x+0.01)で済む。分母がゼロになる組合せをスキップする最低限の関数定義も難しくはないので以下示しておく。使い方はmct(x)とするだけである。
mct()
mct <- function(x) {
L <- NROW(x)
X <- 0
N <-0
for (i in 1:(L-1)) {
for (j in (i+1):L) {
s <- (x[i,j]+x[j,i])
if (s>0) {
N <- N+1
X <- X + (x[i,j]-x[j,i])^2/s }}}
return(list(X2=X, df=N, p=(1-pchisq(X, N))))
}もう少し深く考えると,拡張マクネマー検定の帰無仮説が,本質的に,周辺度数の均質性(というか変化の対称性)であると考えれば,別のアプローチが可能になる。これについては,さまざまな方法が提案されていて,Sun and Yang (2008)によってSASのフォーラムで発表された文書104によると,SASではその1つであるBhapkar’s testがCATMODプロシージャのREPEATEDステートメントに実装されていると書かれている。一般論としてはStuart-MaxwellよりもBhapkarの方が検出力が高いとのことである。
Rではirrパッケージにbhapkar()という関数として実装されている。典拠となる論文はBhapkar (1966)105である。bhapkar()の引数は集計後の正方行列ではなく,集計前の2つの変数(本質的には順序付きカテゴリ変数であるべきと思われるが,ファクター型でも整数型も構わない)からなるデータフレームか行列でなければならない点に注意が必要だが,これを使えば,対称の位置にある変化の和がゼロである場合が含まれていても,問題なく計算できる。
Sun and Yang (2008)の表4に示されているデータを使って分析してみる。元の出典はWalker (2002)の例18.2とのことである。ある種の高脂肪食品への渇望を感じる頻度を3段階(まったく,時々,頻繁に)で尋ね,2週間の試験食治療を行う前後で比較した結果である。
| まったく(後) | 時々(後) | 頻繁に(後) | |
|---|---|---|---|
| まったく(前) | 14 | 6 | 4 |
| 時々(前) | 9 | 17 | 2 |
| 頻繁に(前) | 6 | 12 | 8 |
これを使って拡張McNemar検定やBhapkarの検定をするコードは以下である。
# https://works.bepress.com/zyang/17/download/
# (In Table 4, SAS's gMcNemar gives the results below)
# GMN=6, DF=2, PROBCHI=0.0497871, QCHI95=5.9914645, QCHI99=9.2103404
# (Bhapkar's test in CATMOD give the results below)
# Intercept: DF=2, Chi-Sq=379.45, Pr>Chisq=<.0001
# symp: DF=2, Chi-Sq=6.50, Pr>Chisq=0.0388
# http://www.people.vcu.edu/~dbandyop/BIOS625/GenMcNemar.pdf
# in http://www.people.vcu.edu/~dbandyop/BIOS625.18.html (Lecture 17)
dat <- matrix(c(14, 9, 6, 6, 17, 12, 4, 2, 8), 3, 3)
rownames(dat) <- c("Never", "Occasional", "Frequent")
colnames(dat) <- c("Never", "Occasional", "Frequent")
mcnemar.test(dat)
# Bhapkar's test can be done for raw data.
if (require(irr)==FALSE) {
install.packages("irr", dep=TRUE)
library(irr)
}
BEFORE <- rep(1:NCOL(dat), dat[,1])
for (i in 2:NCOL(dat)) {
BEFORE <- c(BEFORE, rep(1:NCOL(dat), dat[, i]))
}
dx <- data.frame(
after = factor(rep(1:NROW(dat), colSums(dat)), labels=colnames(dat)),
before = factor(BEFORE, labels=rownames(dat))
)
bhapkar(dx)結果は下枠内の通りに得られる。
> mcnemar.test(dat)
McNemar's Chi-squared test
data: dat
McNemar's chi-squared = 8.1429, df = 3, p-value = 0.04315
> bhapkar(dx)
Bhapkar marginal homogeneity
Subjects = 78
Raters = 2
Chisq = 6.5
Chisq(2) = 6.5
p-value = 0.0388 マクネマー検定の結果がSASと違うのは,Rのmcnemar.test()関数がデフォルトで連続性の補正をしているためである。SASと同じ結果を得るにはcorrect=FALSEオプションを付ければ良い。Bhapkarの検定結果はSASと一致している。
ここで,仮に「頻繁に→まったく」と「まったく→頻繁に」がともにゼロであった場合を考えてみる。コードは以下。
# if Both Frequent -> Never and Never -> Frequent were 0
dat[3,1] <- dat[1,3] <- 0
mcnemar.test(dat)
mcnemar.test(dat+0.01)
mct(dat)
BEFORE <- rep(1:NCOL(dat), dat[,1])
for (i in 2:NCOL(dat)) {
BEFORE <- c(BEFORE, rep(1:NCOL(dat), dat[, i]))
}
dx <- data.frame(
after = factor(rep(1:NROW(dat), colSums(dat)), labels=colnames(dat)),
before = factor(BEFORE, labels=rownames(dat))
)
bhapkar(dx)対角成分の和がゼロになる組み合わせが存在するため,マクネマー検定のカイ二乗値はNaNとなり,p値が計算できないが,Bhapkarの検定は普通にできる。なお,すべてのセルに0.01を加えてマクネマー検定を実行するとp値が0.05よりわずかに大きくなるが,ゼロになる組み合わせをスキップするmct()関数ではp値が0.02前後であり,Bhapkarの検定結果に近い。この結果を踏まえれば,全セルに小さな定数を加える方法は妥当でない可能性があり,スキップするかBhapkarの検定を使うべきと考えられる。
> mcnemar.test(dat)
McNemar's Chi-squared test
data: dat
McNemar's chi-squared = NaN, df = 3, p-value = NA
> mcnemar.test(dat+0.01)
McNemar's Chi-squared test
data: dat + 0.01
McNemar's chi-squared = 7.7319, df = 3, p-value = 0.05189
> mct(dat)
$X2
[1] 7.742857
$df
[1] 2
$p
[1] 0.02082859
> bhapkar(dx)
Bhapkar marginal homogeneity
Subjects = 68
Raters = 2
Chisq = 8.74
Chisq(2) = 8.74
p-value = 0.0127 新しい検査方法を開発する際は,感度(sensitivity)と特異度(specificity)が優れていることが必要である。
感度と特異度の計算に必要なデータは,元々カテゴリデータの場合は,その検査で陽性か陰性かと,信頼性が確立した標準的な方法(gold standard)による確定診断として真にその病気かどうかである。
データさえあれば、感度や特異度、診断正確度(Diagnostic Accuracy)などの計算は簡単で、下記の定義により、割り算するだけで求められる。また、陽性的中率(Positive Predictive Value: PPV)、陰性的中率(Negative Predictive Value: NPV)は、純粋な検査性能の指標ではなく、実際のスクリーニングをしたとき(つまり、真の疾病の有無が未知であるとき)に、陽性あるいは陰性という判定結果がどれくらい当たっているかを意味するため、有病割合に依存して変わる、検査実施の有効性の指標といえる。
| 確定診断による病気の有無 | |||
|---|---|---|---|
| 病気 | 健康 | ||
| 検査結果 | 陽性 | a人 | b人 |
| 陰性 | c人 | d人 | |
感度や特異度の点推定は母比率の推定そのものなので、信頼区間の推定も正規近似や二項分布を使った正確な推定が可能である。手計算では面倒だが、EZRでは「定性検査の診断への正確度の評価」メニューから、分割表に直接入力すれば計算してくれる。epiRパッケージのepi.tests()関数を使っているので、正規近似でなくClopper-Pearson法による正確な95%信頼区間が自動的に表示される。
数式を示しておくと、サイズNのうち事象ありの数をXとすると、母比率の点推定値pˆはpˆ=X/Nであり、その(1-α)信頼区間(例えばαが0.05であれば95%信頼区間)は、正規近似では(注:初等統計のテキストで示されているこの式は、DescToolsパッケージのBinomCI()関数のmethod="wald"、あるいはepitoolsパッケージのbinom.approx()関数に実装されているWaldの方法であり、prop.test()関数のcorrect=FALSEで得られる信頼区間は、正規近似とはいえ、epitoolsパッケージのbinom.wilson()、またはBinomCI()関数のデフォルトでありmethod="wilson"で明示的に指定できる結果とも一致する通りWilsonの方法によっているので結果が異なる)、正規分布のaパーセント点をZaと書くことにすれば、
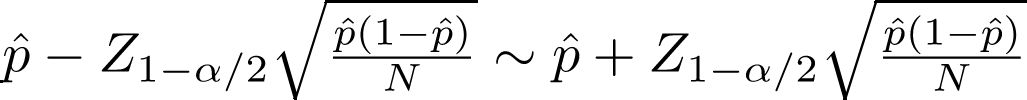
となり、Clopper-Pearson法による正確な信頼区間は、第1自由度d1、第2自由度d2のF分布のaパーセント点をFa(d1, d2)と書くことにすれば、
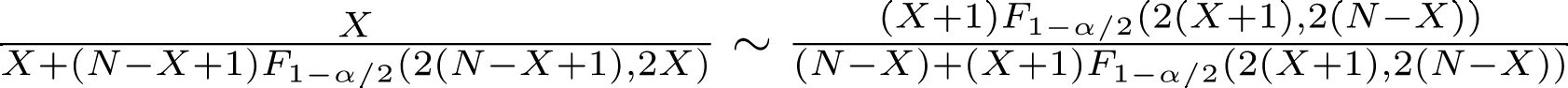
となる。Rで関数定義をすれば以下の通り。
ss <- function(X, N, .Exact=FALSE, .CI=0.95) {
pp <- X/N
ppl <- ifelse(.Exact, X / (X+(N-X+1)*qf(1-(1-.CI)/2, 2*(N-X+1), 2*X)),
pp-qnorm(1-(1-.CI)/2)*sqrt(pp*(1-pp)/N) )
ppu <- ifelse(.Exact, (X+1)*qf(1-(1-.CI)/2, 2*(X+1), 2*(N-X)) /
((N-X)+(X+1)*qf(1-(1-.CI)/2, 2*(X+1), 2*(N-X))),
pp+qnorm(1-(1-.CI)/2)*sqrt(pp*(1-pp)/N) )
return(sprintf("%4.3f (%4.3f-%4.3f)", pp, ppl, ppu))
}近年、2つの定性検査の性能を比較する論文(例えばこれ)がいくつか出ていて、感度、特異度、診断正確度についての比較をマクネマーの検定、陽性的中率と陰性的中率についての比較をフィッシャーの正確な検定でしているものが多い。手順を工夫すればEZRでもできるが、コードを書いてしまう方が楽であろう(https://minato.sip21c.org/t2ct.Rとして開発中}。
データが元々連続量の場合に必要なのは,検査値とgold standardで真にその病気かどうかという情報の2つである。しかし,通常,連続量である検査値がいくつだったら陽性と判定したら良いのかはわからない。そこで,その閾値を統計学的に根拠のある決め方をするために使える方法がROC分析である。
ROC (Receiver Operating Characteristic)分析とは,検査で陽性/陰性を判別する閾値を段階的に変え,感度が1に,(1-特異度)が0に最も近い結果を与える値を最適閾値として求めるものである。通常,(1ー特異度)を横軸,感度を縦軸にとって閾値を変えて得られる値を曲線で結ぶ(ROC曲線と呼ばれる)。
複数の検査方法をROC分析で比較することもでき,ROC曲線の下の面積(AUC; Area Under the Curve)が最も大きい方法が,最も性能が良い方法と判定される。実際にその方法を採用するかどうかは,性能が優れているだけでは不十分で,コストや実施のしやすさなども考慮される
マラリアには何種類もRDT(迅速診断キット)がある。元々,マラリア患者の他の熱病患者と区別するために開発されたもので,熱のある患者は血中の原虫感染強度が強いことから,特異度が高いことが重要であり,感度は中程度で良かった。
しかし近年では,原虫感染強度が弱いときの積極的疫学調査(症状がない一般住民を対象とした検査)にも用いられるようになってきた。例えば,ソロモン諸島での三日熱マラリアについてPan-R malariaを使った検査結果は,以下のように得られた(指先穿刺で得た同じ血液サンプルをギムザ染色で確定診断した結果、三日熱マラリア原虫が検出された23人のうちPan-R陽性が7人、検出されなかった159人のうちPan-R陽性が3人)ので,感度が不十分であることがわかった。
EZRで実施するには,「統計解析」「検査の正確度の評価」「定性検査の診断への正確度の評価」を選び,表示される分割表に該当する数値を入力すればよい。
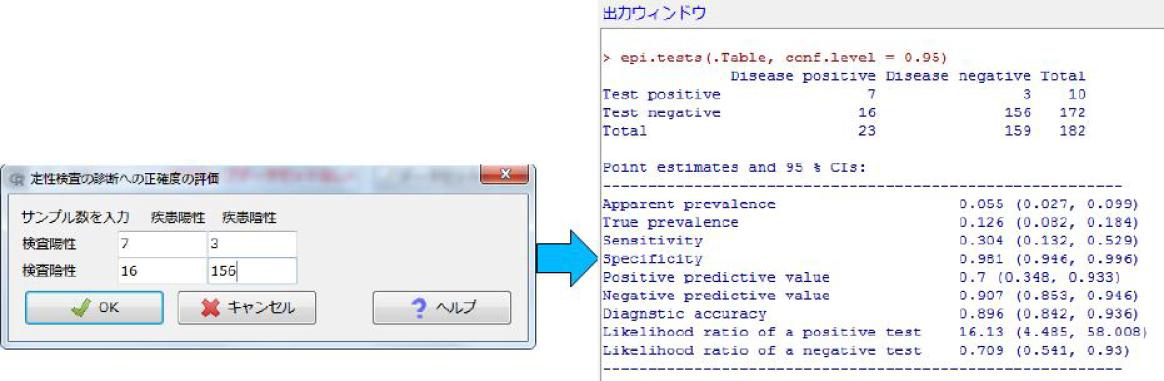
質問紙に基づいたうつ得点により,うつ病のスクリーニングを行う際に必要なことは,臨床診断でうつ病とわかっている患者と,うつ病でないとわかっている患者(または健康なボランティア)の両方を対象にし,対象者全員について,同じ質問紙によって,尺度得点の合計としての「うつ得点」を得て,ROC分析を実行することである。
| ID | うつ得点 | 臨床診断 |
|---|---|---|
| 1 | 20 | うつ |
| 2 | 13 | 非うつ |
| 3 | 19 | 非うつ |
| 4 | 21 | 非うつ |
| 5 | 22 | うつ |
| 6 | 28 | うつ |
| 7 | 11 | 非うつ |
| 8 | 25 | 非うつ |
| 9 | 16 | 非うつ |
| 10 | 19 | 非うつ |
この質問紙得点におけるうつの診断基準が,「18点以上を陽性と判定する」とすると,診断のためのクロス集計表は以下のようになり,感度は1 (3/3)で,特異度は約0.43 (3/7)となることがわかる。
| うつ | 非うつ | |
|---|---|---|
| 陽性 | 3 | 4 |
| 陰性 | 0 | 3 |
この基準値では感度は高いが,特異度が低いことがわかる。基準値を変えることにより,感度と特異度がどちらも高くなるような点を探索することができるというのがROC分析の考え方である。
EZRで実行するには,まず「ファイル」「新しいデータセットを作成する(直接入力)」から下図のようにデータを入力する106。アルファベット順で先に出現する方が陰性になるため,[Dep]と[Norm]だと[Dep]が陰性扱いになってしまう。そのため,ここでは[1.Dep]と[0.Norm]入力として[Norm]が陰性として扱われるようにした。
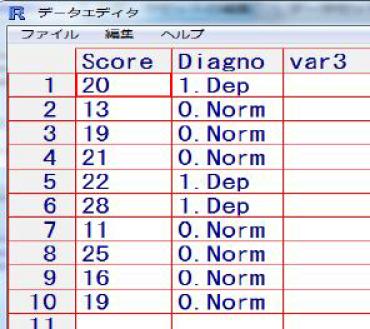
「統計解析」[検査の正確度の評価」「定量検査の診断への正確度の評価(ROC曲線)」から変数を選んで[OK]をクリック 「20以上がうつ」という基準で最適な感度(1.0)と特異度(0.714)が得られた。曲線下面積(AUC)は0.8571,95%CIが 0.6044から1まで (DeLong法) とわかる。
同じモノを評価するための2つの異なった検査の結果は異なりうる。ROC分析の結果として計算されるAUCにより,性能を比較することが可能である(AUCが大きいほど高性能といえる)。
EZRが内部で使っているpROCパッケージのマニュアルに書かれているように、pROCパッケージのroc.test()関数では、method=オプションを"delong"、"bootstrap"、"venkatraman"のいずれか指定することで比較方法を指定でき、method=オプションが省略された場合は自動的に適切な方法が使われる。"delong"と"bootstrap"がAUCを比較しているのに対して、"venkatraman"はROC自体を比較する方法と書かれている。EZRはmethod=を指定していないが、この例では"delong"が適用されている。
EZRでは,「ファイル」「データのインポート」「ファイルまたはクリップボード,URLからテキストデータを読み込む」で,データセット名をcomptwo,データファイルの場所をインターネットのURL,フィールド区切りをタブにしてOKし,URLとしてhttps://minato.sip21c.org/ROC1.txtを指定する。
注意すべき点は,データセット名としてROC1とROC2は使ってはいけないということである(ファイル名はOK)。もし使うと計算途中でデータセットが上書きされてエラーになる。
「統計解析」「検査の正確度の評価」「2つのROC曲線のAUCの比較」を選び,Marker1とMarker2を選んでOKボタンをクリックすると,以下の結果が得られる。5%水準で統計学的に有意な差があるとはいえない。
Z = -0.0981, p-value = 0.9218
AUC of roc1 AUC of roc2
0.8928571 0.9017857 新しく安価あるいは迅速な測定方法を開発したとき,その測定方法が信頼できるかどうかを検討するには,同じ対象者を,従来gold standardであると考えられてきた方法で測定し,一致しているかをみる。
3つの方法が可能である。
BAプロットをするには,「変数の操作」で,新しい変数として,検討したい2つの変数の差の変数Dと,2つの変数の平均値の変数Mを作成し,横軸にM,縦軸にDをとった散布図を描けば良いが,RにはBAプロットを実行する機能を関数として実装したパッケージがいくつもある。
MethCompパッケージのBA.plot()関数は便利である。MethCompパッケージに含まれているデータoxは,子供61人の血中酸素飽和度を血液ガス測定(CO)とパルスオキシメータ測定(pulse)で測定した結果である。用例は下記の通り。
> library(MethComp)
> data(ox)
> BA.plot(ox)MethComp以外のパッケージとしては,blandrがお薦めできる。GitHub上のhttps://github.com/deepankardatta/blandr/で開発されており,グラフィクスとしてbaseだけでなくgrid系もサポートされているようである(blandr.draw()関数では,plotter="rplot"オプションを指定しないとggplot2を使った描画になる)。
Bland自身が管理しているサイト108で公開されている,Bland and Altman (1986)にも使われているデータがいくつかあり,このパッケージにはそれらをダウンロードするための関数が含まれている。MethCompと同じく酸素飽和度のデータを読み込む関数はblandr.dataset.o2sats()であり,血中酸素飽和度をより簡便なパルスオキシメータと酸素飽和度計で測定した結果とあるが109,MethCompパッケージに入っているoxとは人数が異なる。
Bland-Altmanプロットを実行させる関数は,blandr.draw(method1, method2)という形で実行する。method1,method2は,それぞれの方法で測定した結果の数値ベクトルである。また,2つの方法の相関係数を計算し,対応のあるt検定の結果を求めると同時に散布図を描きx=yの直線と回帰直線を描く関数はblandr.method.comparison(method1, method2)である。また,blandr.output.text(method1, method2)関数を使うと,平均値やバイアスなどの情報を数値として表示させることができる。これらの関数をBlandの酸素飽和度データに適用するコードと結果を示す。
if (require(blandr)==FALSE) {
install.packages("blandr", dep=TRUE)
library(blandr)
}
o2 <- blandr.dataset.o2sats() # read data via internet
# draw Bland-Altman plot
blandr.draw(o2$pos, o2$osm, plotter="rplot")
# calculate correlation coefficient and paired t-test, draw scattergram
blandr.method.comparison(o2$pos, o2$osm)
# show the values of Bland-Altman plot
blandr.output.text(o2$pos, o2$osm)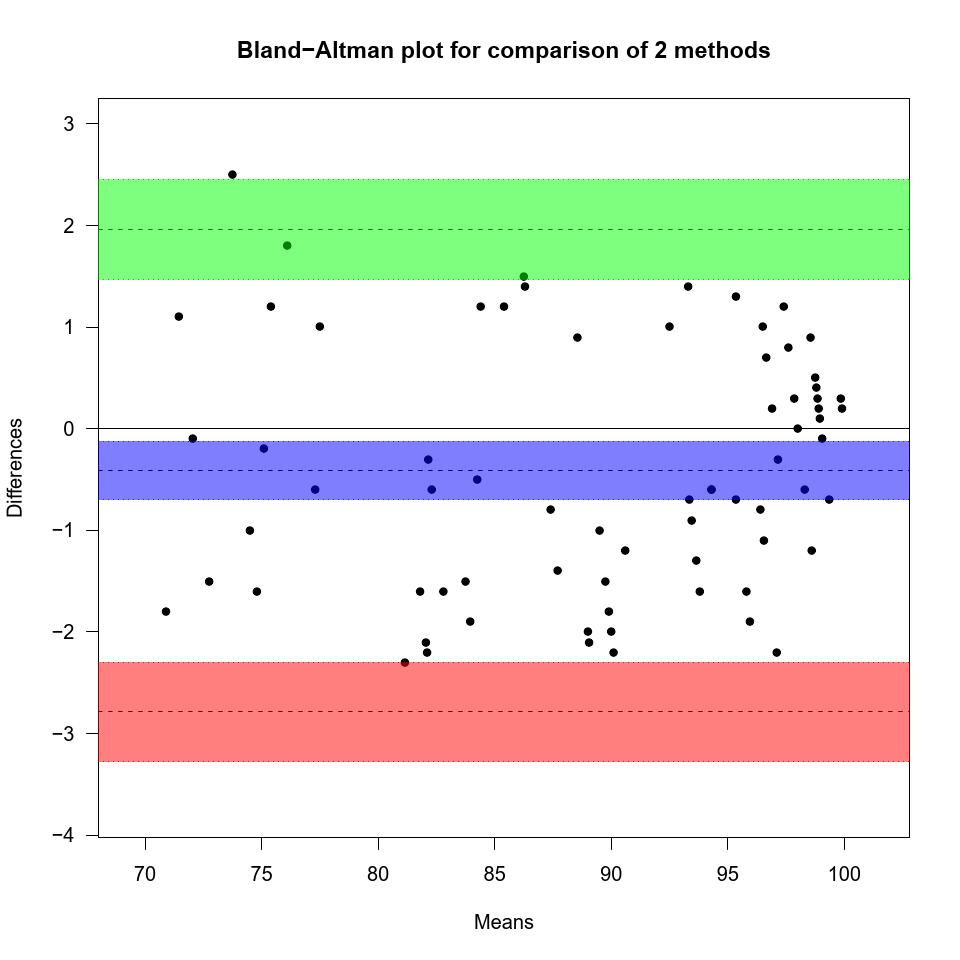
> blandr.method.comparison(ox$pos, ox$osm)
Note as per Bland and Altman 1986 linear correlation DOES NOT mean agreement.
Data which seem to be in poor agreement can produce quite high correlations.
Line of equality in dashed black, linear regression model in solid red.
Paired T-tests evaluate for significant differences between the means of two
sets of data. It does not test agreement, as the results of a T-test can be
hidden by the distribution of differences. See the references for further reading.
Paired T-test p-value: 0.005096854
Correlation coefficients only tell us the linear relationship between 2 variables
and nothing about agreement.
Correlation coefficient: 0.9904082
Linear regression models, are conceptually similar to correlation coefficients,
and again tell us nothing about agreement.
Using method 1 to predict the dependent method 2, using least squares regression.
Regression equation: method 2 = 0.9980026 x method 1 + -0.2337408 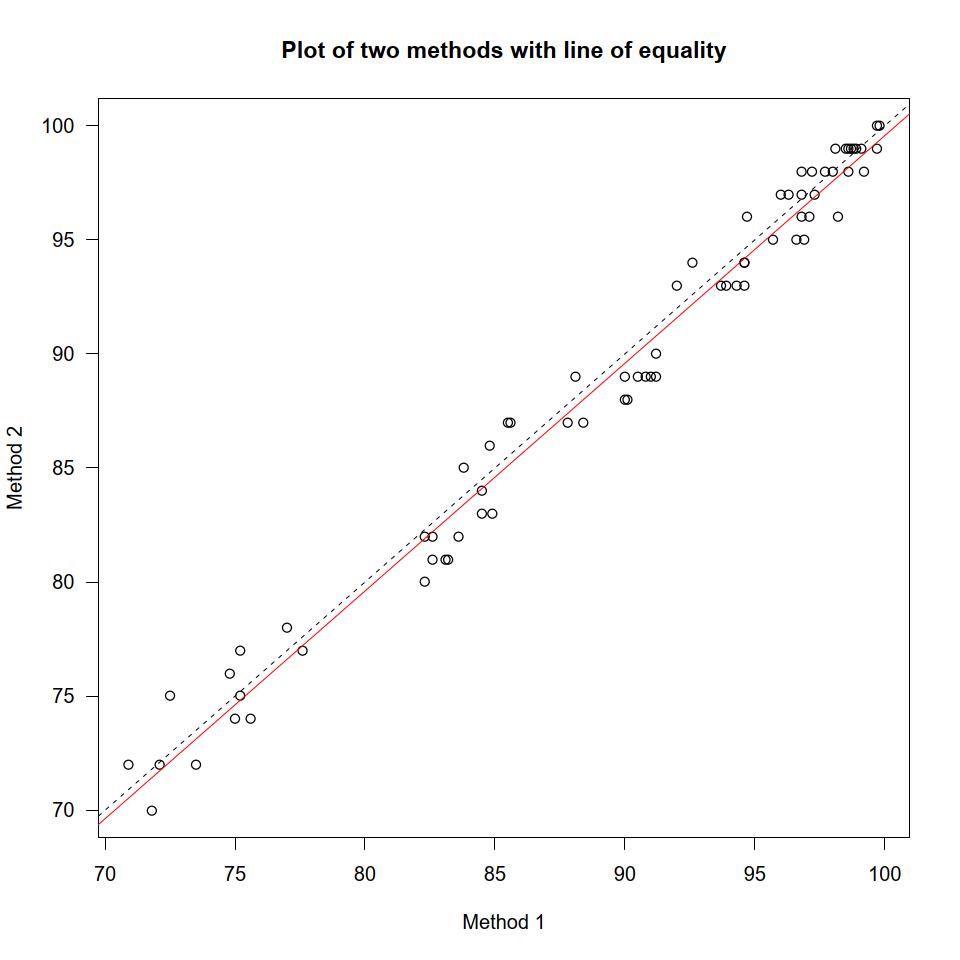
> blandr.output.text(ox$pos, ox$osm)
Number of comparisons: 72
Maximum value for average measures: 99.9
Minimum value for average measures: 70.9
Maximum value for difference in measures: 2.5
Minimum value for difference in measures: -2.3
Bias: -0.4125
Standard deviation of bias: 1.210859
Standard error of bias: 0.1427011
Standard error for limits of agreement: 0.245005
Bias: -0.4125
Bias- upper 95% CI: -0.1279621
Bias- lower 95% CI: -0.6970379
Upper limit of agreement: 1.960784
Upper LOA- upper 95% CI: 2.44931
Upper LOA- lower 95% CI: 1.472258
Lower limit of agreement: -2.785784
Lower LOA- upper 95% CI: -2.297258
Lower LOA- lower 95% CI: -3.27431
Derived measures:
Mean of differences/means: -0.4711187
Point estimate of bias as proportion of lowest average: -0.5818054
Point estimate of bias as proportion of highest average -0.4129129
Spread of data between lower and upper LoAs: 4.746567
Bias as proportion of LoA spread: -8.690491
Bias:
-0.4125 ( -0.6970379 to -0.1279621 )
ULoA:
1.960784 ( 1.472258 to 2.44931 )
LLoA:
-2.785784 ( -3.27431 to -2.297258 ) なお,BAプロットの詳細な解説としては,Bland JM, Altman DG: Measuring agreement in method comparison studies. Statistical Methods in Medical Research, 1999; 8 (2): 135-160.110がわかりやすい。
非常に難しい。統計学的な考え方の非常に洗練された理解を要する。修得するには,おそらくかなりの努力が必要であろう。
そのため,本テキストでは概要だけ説明するが,メタアナリシスの結果は,多くの研究で共通してみられる知見を明らかにするので,エビデンスベーストメディシン(EBM)で最高レベルのエビデンスを提供すると言われている。
教科書としては,丹後俊郎『メタアナリシス入門:エビデンスの統合を目指す統計手法』朝倉書店,2002年をお薦めするが,論文を書くには,PRISMAガイドラインに沿っていることが重要である。2009年版チェックリストは邦訳もあるが,最新の2020年版(チェックリスト,各項目の説明がついた拡張版チェックリスト)を英語で読むのが良いだろう。
まず,「メタ」は何を意味するか? について考えてみよう。言語としては,後で発生し,より包括的な何かで,オリジナルのものを批判的に取り扱う,新しいけれども関連した専門分野を名付けるときにしばしば使われるとされる(Eggerら, 1997)。コミュニケーションに対してメタコミュニケーション,文字に対してメタ文字,言語に対してメタ言語,マーケティングに対してメタマーケティング等は好例である。
統計解析において,メタアナリシスとは,多くの先行研究の結果を統合する手法の1つであり,概ね次のステップを踏む。
先行研究の結果を統合/総合しようという試み自体は新しくない。Wright卿 (1896) は,チフスに対する新しいワクチンを開発し,いくつかの異なる集団において同じワクチンの有効性を検査したが,Karl Pearson (1904) は,それまでに使われたワクチンの有効性をレビューして再評価した。これがメタアナリシスの先駆けと言われている。
| StudyName | RecovV | DiedV | TotalV | RecovNV | DiedNV | TotalNV |
|---|---|---|---|---|---|---|
| HospitalSA | 30 | 2 | 32 | 63 | 12 | 75 |
| GarrisonLadysmith | 27 | 8 | 35 | 1160 | 329 | 1489 |
| SpecialRegimenSA | 63 | 9 | 72 | 61 | 21 | 82 |
| SpecialHospitalSA | 1088 | 86 | 1174 | 4453 | 538 | 4991 |
| MilitaryHospitalSA | 701 | 63 | 764 | 2864 | 510 | 3374 |
| IndianArmy | 73 | 11 | 84 | 1052 | 423 | 1475 |
データは https://minato.sip21c.org/Pearson1.txtにアップロードしてある。各研究について,四分相関係数を計算する(注:EZRメニューにはないが,library(psych)のtetrachoric()か,library(polycor)のpolychor()を使用すれば可能)。
> tetrachoric(matrix(c(30,2,63,12),2,2)) # 結果は 0.31
> polychor(matrix(c(30,2,63,12),2,2)) # 結果は0.30697276つの研究の四分相関係数の平均を計算すると,0.193となる
mean(c(0.307, -0.010, 0.300, 0.119, 0.194, 0.248))
Pearsonの結論「この効果はワクチンとして推奨するには小さすぎ」
通常,相関係数をまとめるには単純平均ではなく,フィッシャーのZ変換とサンプルサイズによる重み付けをする111。この事例は普通の相関係数ではなく四分相関係数なので,Z変換で良いのかは定かでないが,以下方法を示す。
固定効果モデル,即ち相関係数の母数はすべての研究に共通で,研究間の差はランダムエラーであると仮定するモデルでは, Z = 0.5 ln{(1+r) / (1-r)} で変換すると,Z相関係数の分散が1/(n − 3)となる。分散の逆数を重みとしたZ相関係数の重み付き平均Mを求め,その標準誤差SEmが分散の逆数の和の逆数の平方根として得られることから,95%信頼区間の上限と下限をM ± 1.96 SEmとして求め,これらをZ変換の逆変換 R = {exp(2Z)-1} / {exp(2Z)+1} を使って元に戻す。
https://minato.sip21c.org/ebhc/pooledr.R
pooledr <- function(rs, Ns, pCI=0.975) {
Zconv <- function(r) { 0.5*log((1+r)/(1-r)) }
revZ <- function(Z) { (exp(2*Z)-1)/(exp(2*Z)+1) }
R <- Zconv(rs)
W <- Ns-3
M <- sum(R*W)/sum(W)
SE <- sqrt(1/sum(W))
LLM <- M-qnorm(pCI)*SE
ULM <- M+qnorm(pCI)*SE
R <- revZ(M)
LLR <- revZ(LLM)
ULR <- revZ(ULM)
return(list(R=R, pCI=pCI, CI=c(LLR, ULR)))
}
r <- c(0.307, -0.010, 0.300, 0.119, 0.194, 0.248)
N <- c(32+75, 35+1489, 72+82, 1174+4991, 764+3374, 84+1475)
pooledr(r, N)結果として得られる値は以下の通りであり,相関は0ではないがごく弱いと考えられる。ただ,この事例では四分相関係数がマイナスの研究も含まれており,おそらく固定効果モデルは正しくない。
> pooledr(r, N)
$R
[1] 0.1462674
$pCI
[1] 0.975
$CI
[1] 0.1297990 0.1626551変量効果モデルでは,研究間の分散にランダムエラーでは説明できない分散を仮定して計算する。理論も計算式もかなり面倒なので省略するが,Rではmetaforパッケージを使えば計算できると前掲書(岡田・小野寺, 2018)に書かれている。
それぞれの研究結果は,オッズ比を用いても評価可能である。例えば,(30/2)/(63/12)は2.86となる。これは,最初の研究ではワクチン接種の結果生存可能性が2.86倍になったことを意味する。なお,fisher.test(matrix(c(30, 2, 63, 12), 2, 2)) の出力するオッズ比は2.83だが,これは計算が最尤推定によるためである。
6つの研究結果からマンテル=ヘンツェルの要約オッズ比を計算するには,metaパッケージを使うのが簡単である。コードは下記の通り(実行するとカレントディレクトリにグラフを含むpdfファイルができてしまうので注意)。
dat <- read.delim("https://minato.sip21c.org/Pearson1.txt")
library(meta)
print(res <- metabin(RecovV, TotalV, RecovNV, TotalNV, studlab=StudyName, data=dat, sm="OR"))
pdf("meta-analysis-vaccine.pdf", width=12, height=8)
forest(res)
drapery(res, type="pval")
dev.off()metaパッケージのmetabin()関数により,以下の結果が得られる。固定効果モデルによるマンテル=ヘンツェルの要約オッズ比は1.77(95%信頼区間は1.50-2.08)で,I2が26.4%,コクランのQ検定の結果のp値が0.24と有意でないので,研究間の有意な異質性はなく,固定効果モデルで解析しても良いことになる。先にフィッシャーのZ変換を使って四分相関係数をサンプルサイズで重み付けしたときは,固定効果モデルはおそらく正しくないと議論したが,オッズ比で考えると,偶然のばらつきと考えても良いレベルの異質性であったと考えられる。なお,このコードではフォレストプロットの補足的に使って良いとされるDraperyプロットも描画される。各研究のp値関数が灰色で,要約オッズ比のp値関数が青(固定効果モデル)または赤(変量効果モデル)で示されている。
Number of studies combined: k = 6
Number of observations: o = 13647
Number of events: e = 11635
OR 95%-CI z p-value
Common effect model 1.7659 [1.4979; 2.0820] 6.77 < 0.0001
Random effects model 1.7854 [1.4258; 2.2356] 5.05 < 0.0001
Quantifying heterogeneity:
tau^2 = 0.0186 [0.0000; 0.8188]; tau = 0.1362 [0.0000; 0.9049]
I^2 = 26.4% [0.0%; 69.4%]; H = 1.17 [1.00; 1.81]
Test of heterogeneity:
Q d.f. p-value
6.80 5 0.2362
Details on meta-analytical method:
- Mantel-Haenszel method
- Restricted maximum-likelihood estimator for tau^2
- Q-profile method for confidence interval of tau^2 and tau要約統計量としてマンテル=ヘンツェルの要約オッズ比だけなら,fmsbパッケージのORMH()関数でも計算できるが,metaパッケージのmetabin()は,sm="OR"で要約オッズ比を計算するだけでなく,sm="RR"と指定すれば要約リスク比を,sm="RD"とすれば要約リスク差を計算できる(もちろん元データがコホート研究かRCTでなくては無意味だが)。
プール化の方法も,ORMH()はマンテル=ヘンツェルの方法だけだが,metabin()ではmethod="Inverse"オプションにより逆分散重み付け法(Fleiss, 1993),method="Peto"でPetoの方法(Yussuf et al., 1985),method="SSW"でサンプルサイズ法(Bakbergenuly et al., 2020)が適用される。
なお,Huedo-Medina T et al. (2006)によると,コクランのQ統計量を使ったQ検定でもI2指標を使っても,研究数が少ない場合の欠点である異質性の検出力の小ささは解決できないとのことである。
EZRでは「ファイル」「データのインポート」からURLとしてhttps://minato.sip21c.org/Pearson1.txtを入力してデータを読み込んでおき,「統計解析」「メタアナリシスとメタ回帰」「比率の比較のメタアナリシスとメタ回帰」から「研究の名前を示す変数」としてStudyName,「テスト群のイベント発生数を示す変数」としてRecovV,「テスト群の総サンプル数を示す変数」としてTotalV,「コントロール群のイベント発生数を示す変数」としてRecovNV,「コントロール群の総サンプル数を示す変数」としてTotalNVを選び,統合する項目の指定を「オッズ比」にして「OK」をクリックすると,フォレストプロットとともに6つの研究結果を統合したオッズ比や異質性指標がグラフィックウィンドウに表示される。固定効果モデルで1.77,ランダム効果モデルで1.79とわかる(ともに有意水準5%で統計学的に有意に1より大きい)。
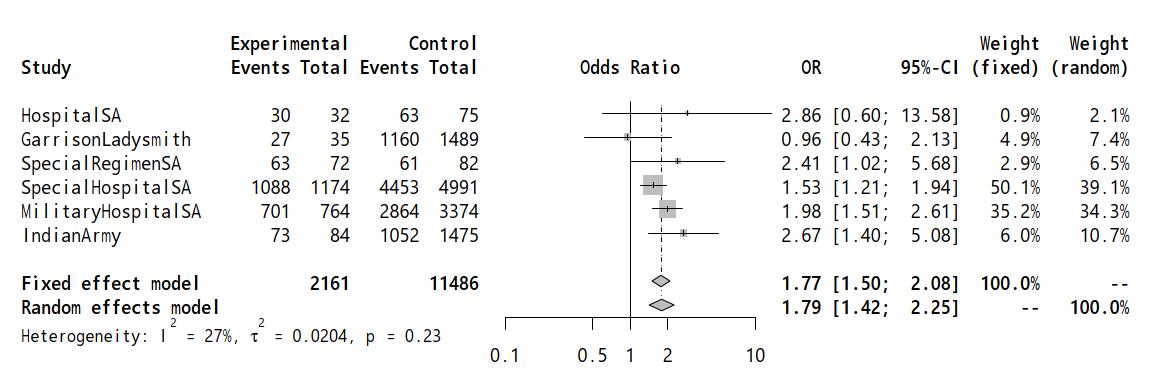
フォレストプロットは,結果を一覧するのに便利であり,論文投稿にも含めるのが普通である。また,EZRでは,「比率の比較のメタアナリシスとメタ回帰」の他,「平均値の比較のメタアナリシスとメタ回帰」と「ハザード比のメタアナリシスとメタ回帰」メニューが提供されている。
生存時間解析はRcmdr本体には入っていない。しかし,プラグインが2種類発表されているし,EZRには入っている。プラグインの1つはJohn Fox教授自身が開発したRcmdrPlugin.survivalであり,もう1つはDr. Daniel C. Leucutaというルーマニアの研究者が開発したRcmdrPlugin.SurvivalTである112。いずれも,survivalパッケージの機能の基本的なものに対して,グラフィカルなユーザーインターフェースを提供するものである。ここでは,Rコンソールで次のように打ち,前者をインストールしたものとする。
install.package(RcmdrPlugin.survival)生存時間解析を十分説明するには,それだけで1冊の本が必要だが,Rのsurvivalパッケージでは,生存時間解析を実行するための多くの関数が提供されており,かなり高度な解析まで実行できる。
Rcmdrの[ツール]から[プラグインのロード]を選んでRcmdrPlugin.survivalを選んで[OK]をクリックすると,Rcmdrを再起動するかどうか聞いてくるので,[はい]をクリックすると,次のような生存時間解析関係のメニューがRcmdrに追加された状態になる(以下,この状態を“Rcmdr+RcmdrPlugin.survival”と表記する):「データ」の「Survival data」,「統計量」の「Survival analysis」,「モデルへの適合」のいくつかの項目,「モデル」の「グラフ」のいくつかの項目,「モデル」の「数値による診断」の「Test proportional hazards」である。
EZRには生存時間解析が含まれていて,「統計解析」の「生存期間の解析」から様々な分析が実行できる。
実験においては,化学物質などへの1回の曝露の影響を時間を追ってみていくことが良く行われる。時間ごとに何らかの量の変化を追うほかに,エンドポイントを死亡とした場合,死ぬまでの時間を分析することで毒性の強さを評価することができる。このような期間データを扱う方法としては,一般に生存時間解析(Survival AnalysisまたはEvent History Analysis)と呼ばれるものがある。なかでもよく知られているものがKaplan-Meierの積・極限推定量である(現在では一般に,カプラン=マイヤ推定量と呼ばれている)。カプラン=マイヤ推定量は,イベントが起こった各時点での,イベントが起こる可能性がある人口(リスク集合)あたりのイベント発生数を1から引いたものを掛け合わせて得られる,ノンパラメトリックな最尤推定量である。また,複数の期間データ列があったときに,それらの差を検定したい場合は,ログランク検定や一般化ウィルコクソン検定が使われる。
それらのノンパラメトリックな方法とは別に,イベントが起こるまでの時間が何らかのパラメトリックな分布に当てはまるかどうかを調べる方法もある。当てはめる分布としては指数分布やワイブル分布がある。中間的なものとして,イベントが起こるまでの期間に対して,何らかの別の要因群が与える効果を調べたいときに,それらが基準となる個体のハザードに対してexp (∑βzi)という比例定数の形で掛かるとする比例ハザード性だけを仮定し,分布の形は仮定しないコックス回帰(比例ハザードモデルとも呼ばれる)は,セミパラメトリックな方法といえる。別の要因群の効果は,パラメトリックなモデルに対数線形モデルの独立変数項として入れてしまう加速モデルによって調べることもできる。
Rでは生存時間解析をするための関数はsurvivalパッケージで提供されており,Rコンソールでlibrary(survival)またはrequire(survival)とタイプしてsurvivalパッケージをメモリにロードした後では,Surv()で生存時間クラスをもつオブジェクトの生成,survfit()でカプラン=マイヤ法,survdiff()でログランク検定,coxph()でコックス回帰,survreg()で加速モデルの当てはめを実行できる。なお,生存時間解析について,より詳しく知りたい方は,大橋,浜田(1995)などを参照されたい。
まず,カプラン=マイヤ推定量についての一般論を示す。イベントが起こる可能性がある状態になってから,イベントが起こった時点をt1, t2, ...とし,t1時点でのイベント発生数をd1,t2時点でのイベント発生数をd2,以下同様であるとする。また,時点t1, t2, ...の直前でのリスク集合の大きさをn1, n2, ...で示す。リスク集合の大きさとは,その直前でまだイベントが起きていない個体数である。
観察途中で死亡や転居などによって打ち切りが生じるために,リスク集合の大きさはイベント発生によってだけではなく,打ち切りによっても減少する。従ってniは,時点tiより前にイベント発生または打ち切りを起こした個体数をn1から除いた残りの数となる(実際は,ti − 1からtiの間に起こった打ち切り数をni − 1 − di − 1から除いたものがniとなり,それを順次繰り返す)。なお,イベント発生と打ち切りが同時点で起きている場合は,打ち切りをイベント発生直後に起きたと見なして処理するのが慣例である。
このとき,カプラン=マイヤ推定量Ŝ(t)は, Ŝ(t) = (1 − d1/n1)(1 − d2/n2)... = ∏i < t(1 − di/ni) として得られる。その標準誤差はグリーンウッドの公式により次の式で分散が得られるので,その平方根となる。 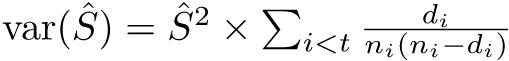
なお,カプラン=マイヤ推定量を計算するときは,階段状のプロットを同時に行うのが普通である。
Rコンソールでは,library(survival)としてパッケージを呼び出し,生存時間を示す数値型変数をTime、1がイベント発生、0が打ち切りである(ただし区間打ち切りの場合は2とか3も使う)整数型の打ち切りフラグを示す変数をFlagとすると、dat <- Surv(Time, Flag)のようにSurv()関数で生存時間データを作り、res <- survfit(dat ~ 1)でカプラン=マイヤ法によるメディアン生存時間が得られる。群分け変数Cによって群ごとにカプラン=マイヤ推定をしたい場合は,res <- survfit(dat ~ C)とすればよい。plot(res)とすれば階段状の生存曲線が描かれる。イベント発生時点ごとの値を見るには,summary(res)とすればよい。
参考までに書いておくと,生データがイベント発生の日付を示している場合,間隔を計算するにはdifftime()関数やISOdate()関数を使う。例えば1964年8月21日生まれの人の今日の年齢はinteger(difftime(ISOdate(2007,6,13),ISOdate(1964,8,21)))/365.24とすれば得られるし,さらに12を掛ければ月単位になる。
例題
survivalパッケージに含まれているデータleukemiaは,急性骨髄性白血病(acute myelogenous leukemia)患者が化学療法によって寛解した後,ランダムに2群に分けられ,1群は維持化学療法を受け(維持群),もう1群は維持化学療法を受けずに(非維持群),経過観察を続けて,維持化学療法が再発までの時間を延ばすかどうかを調べたデータである113。以下の3つの変数が含まれている。
薬物維持化学療法の維持群と非維持群で別々に,再発までの時間の中央値をカプラン=マイヤ推定し,生存曲線をプロットせよ。
Rコンソールでは以下のように実行する。
> library(survival)
> print(res <- survfit(Surv(time,status)~x, data=leukemia))
> plot(res, xlab="(Weeks)", lty=1:2,
+ main="Periods until remission of acute myelogenous leukaemia")
> legend("right", lty=1:2, legend=levels(leukemia$x))2行目でカプラン=マイヤ法での計算がなされ,下枠内が表示される。
records n.max n.start events median 0.95LCL 0.95UCL
x=Maintained 11 11 11 7 31 18 NA
x=Nonmaintained 12 12 12 11 23 8 NAこの表は,維持群が11人,非維持群が12人,そのうち再発が観察された人がそれぞれ7人と11人いて,維持群の再発までの時間の中央値が31週,非維持群の再発までの時間の中央値が23週で,95%信頼区間の下限はそれぞれ18週と8週,上限はどちらも無限大であると読む。
3行目で2群別々の再発していない人の割合の変化が生存曲線として描かれ,4行目で凡例が右端に描かれる。
Rcmdr+RcmdrPlugin.survivalでは,まずsurvivalパッケージ内のleukemiaをアクティブにする。「データ」の「アタッチされたパッケージからデータを読み込む」でleukemiaの方を選ぶだけで良い。EZRでも,ツールからsurvivalパッケージを読み込み,ファイルの「アタッチされたパッケージからデータを読み込む」でleukemiaを選べば良い。
Rcmdrでのカプラン=マイヤ推定は,「統計量」>「Survival analysis」>「Estimate survival function」と進み,“Time or start/end times”として[time]を選び,“Event indicator”として[status]を選ぶ。次にStrataだが,leukemiaデータでMaintained群とNon-maintained群別々にカプラン=マイヤ推定したいときは,ここに表示されている[x]をクリックする。全データを一括して推定したい場合は何もしない114。
このメニューは生存曲線も描いてくれる。“Confidence Intervals”として“Log”,“Log-log”,“plain”,“none”を指定できる。デフォルトは“Log”である(つまり,survfit()関数で,conf.type=オプションを指定しない場合は,summary()で出力される各イベント発生時点の信頼区間は,conf.type="log"として計算される)。大橋・浜田(1995)のp.68の出力を見ると,SASバージョン6 の計算は,conf.type="plain"とした場合と一致していたし,Statistics in Medicineに 1997年に掲載されていたチュートリアル論文での計算(https://minato.sip21c.org/swtips/survival.htmlを参照のこと)は,conf.type="log-log"とした場合と一致した。“Plot confidence intervals”は,常に生存曲線に信頼区間をつけて描画する[Yes]と常に信頼区間は描画しない[No]の他に,[Default]が指定できる。[Default]は,Strataが指定されている場合は[No],Strataが無い場合は[Yes]が指定された場合と同じ動作をする(なお,描画しない場合でも,アウトプットウィンドウには,summary()の結果として,各イベント発生時点での生存確率の信頼区間の値は表示される)。“Confidence level”は信頼水準であり,デフォルトは.95,つまり95%である。ここを.99とすれば99%信頼区間が求められる。“Mark censoring times”にはデフォルトでチェックが入っており,生存曲線のグラフの打ち切り発生時点で短いティックマークがプロットされる。このチェックを外すと打ち切りレコードは描画されない。“Method”は[Kaplan-Meier]の他にも2つ選べ,“Variance Method”も[Greenwood]でない方法も選べるが,ここはデフォルトのままでいいと思う。“Quantiles to estimate”のボックスに[.25,.5,.75]と入っているが,アウトプットウィンドウで.5のところに表示される値が生存時間の中央値として推定されるカプラン=マイヤ推定量である。日本語環境で使う場合に重要なのは,一番下の"部分集合の表現"のボックスに表示されている[<全ての有効なケース>]という文字列を消してから[OK]ボタンをクリックすることである。おそらく,このプラグインパッケージのバグと思われるが,文字列を消さないで[OK]をクリックすると,[<全ての有効なケース>]という文字列そのものがオプションとして渡されてしまいエラーを生じる。
EZRでははデータをアクティブにした後(注:2022年7月現在、survivalパッケージにamlやleukemiaというデータフレームは入っているが、なぜかEZRではデータフレームとして認識されないので、スクリプトウィンドウの1行目にlibrary(survival)、2行目にaml2 <- as.data.frame(aml)と打ってから選んで実行ボタンをクリックすると、aml2というデータを選べるようになる)、メニューの「統計解析」「生存期間の解析」から「生存曲線の記述と群間の比較(ログランク検定)」を選び,「観察期間の変数」としてtime,「イベント,打ち切りの変数」としてstatus,「群別する変数」としてxを選ぶと,カプラン=マイヤ推定とログランク検定を両方やってくれて,生存期間の中央値が維持療法群31ヶ月(95%信頼区間13ヶ月~上限無限大),非維持療法群23ヶ月(95%信頼区間5ヶ月~33ヶ月),ログランク検定の結果はp値が0.0653で5%水準では有意な差があるとはいえない。
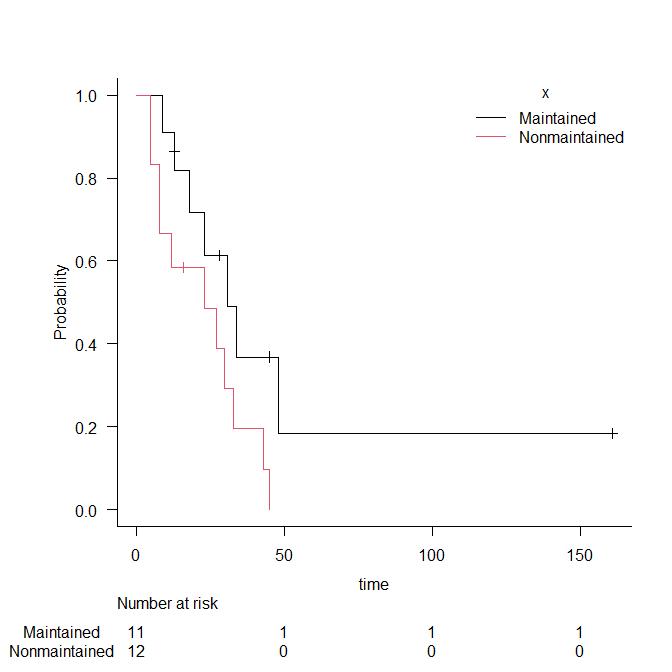
なお、2022年7月現在、survivalパッケージにはcancerという大きながん患者の生存時間データが含まれているが、statusという打ち切りフラグを示す変数が、打ち切りが1、死亡が2となっているので、EZRで解析するためには、予め変数の操作で新しい打ち切りフラグの変数flagを、例えばstatus - 1あるいはifelse(status==2, 1, 0)のようにして、イベント発生が1、打ち切りが0であるように変換しなくてはならない。
次に,ログランク検定を簡単な例で説明する。
8匹のラットを4匹ずつ2群に分け,第1群には毒物Aを投与し,第2群には毒物Bを投与して,生存期間を追跡したときに,第1群のラットが4,6,8,9日目に死亡し,第2群のラットが5,7,12,14日目に死亡したとする。この場合,観察期間内にすべてのラットが死亡し,正確な生存時間がわかっているので,観察打ち切りがないデータとなっていて計算しやすい。
ログランク検定の思想は,大雑把に言えば,死亡イベントが起こったすべての時点で,群と生存/死亡個体数の2×2クロス集計表を作り,それをコクラン=マンテル=ヘンツェル流のやり方で併合するということである。上記の例では,死亡イベントが起こった時点1~8において各群の期待死亡数を計算し,各群の実際の死亡数との差をとって,それに時点の重みを掛けたものを,各時点における各群のスコアとして,群ごとのスコアの合計を求める。2群しかないので,各時点において群1と群2のスコアの絶対値は同じで符号が反対になる。2群の生存時間に差がないという帰無仮説を検定するためには,群1のスコアの2乗を分散で割った値をカイ二乗統計量とし,帰無仮説の下でこれが自由度1のカイ二乗分布に従うことを使って検定する。なお,重みについては,ログランク検定ではすべて1である。一般化ウィルコクソン検定では,重みを,2群を合わせたリスク集合の大きさとする(そうした場合,もし打ち切りがなければ,検定結果は,ウィルコクソンの順位和検定の結果と一致する)。つまり,ログランク検定でも一般化ウィルコクソン検定でも,実は期間の情報はまったく使われず,死亡順位の情報だけが使われている。
記号で書けば次の通りである。第i時点の第j群の期待死亡数eijは,時点iにおける死亡数の合計をdi,時点iにおけるj群のリスク集合の大きさをnij,時点iにおける全体のリスク集合の大きさをniとすると,eij = di ⋅ nij/niと表される。上の例では,e11 = 1 ⋅ n11/n1 = 4/8 = 0.5となる。時点iにおける第j群の死亡数をdij,時点の重みをwiと表せば,時点iにおける群jのスコアuijは, uij = wi(dij − eij) となり,ログランク検定の場合(以下,重みは省略してログランク検定の場合のみ示す)の群1の合計スコアはu1 = ∑idi1 − ei1となる。上の例では,u1 = (1 − 4/8) + (0 − 3/7) + (1 − 3/6) + (0 − 2/5) + (1 − 2/4) + (1 − 1/3) + (0 − 0/2) + (0 − 0/1)である。これを計算すると約1.338となる。
分散は,分散共分散行列の対角成分を考えればいいので,
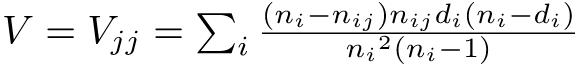 となる。この例の数値を当てはめると,
となる。この例の数値を当てはめると,
 となり,計算すると,約1.568となる。したがって,χ2 = 1.3382/1.568 = 1.14となり,この値は自由度1のカイ二乗分布の95%点である3.84よりずっと小さいので,有意水準5%で帰無仮説は棄却されない。つまりこれだけのデータでは,差があるとはいえないことになる(もちろん,サンプルサイズを大きくすれば違う結果になる可能性もある)。
となり,計算すると,約1.568となる。したがって,χ2 = 1.3382/1.568 = 1.14となり,この値は自由度1のカイ二乗分布の95%点である3.84よりずっと小さいので,有意水準5%で帰無仮説は棄却されない。つまりこれだけのデータでは,差があるとはいえないことになる(もちろん,サンプルサイズを大きくすれば違う結果になる可能性もある)。
Rでは,Surv(time, event)とgroup(注:ここでtimeは生存時間,eventは1がイベント観察,0が観察打ち切りを示すフラグ,groupがグループを示す)を,survdiff()関数に与えることによってログランク検定が実行できる。打ち切りレコードがない場合は,eventは省略できる。なお,生存時間解析の関数はすべてsurvivalパッケージに入っているので,まずlibrary(survival)とすることは必須である。
この例では,Rコンソールでは次のようになる。
> library(survival)
> time <- c(4,6,8,9,5,7,12,14)
> event <- c(1,1,1,1,1,1,1,1)
> group <- c(1,1,1,1,2,2,2,2)
> dat <- Surv(time,event)
> survfit(dat~group)
> survdiff(dat~group)得られる結果の一番下を見ると,χ2 = 1.2,自由度1,p = 0.268となっているので,有意水準5%で,2群には差がないことがわかる。
カプラン=マイヤ法の例題で使ったleukemiaデータで,維持群と非維持群の生存時間に差が無いという帰無仮説をログランク検定するには,Rコンソールでは以下のようにする。
> library(survival)
> survdiff(Surv(time,status)~x, data=leukemia)次の枠内の結果が得られる。p値が0.0653なので,有意水準5%で統計学的に有意な差があるとはいえない。
Call:
survdiff(formula = Surv(time, status) ~ x, data = leukemia )
N Observed Expected (O-E)^2/E (O-E)^2/V
x=Maintained 11 7 10.69 1.27 3.40
x=Nonmaintained 12 11 7.31 1.86 3.40
Chisq= 3.4 on 1 degrees of freedom, p= 0.0653
Rcmdr+RcmdrPlugin.survivalでログランク検定をしたい場合は,leukemiaデータをアクティブにしてから,統計量>Survival analysis>Compare Survival Functionsでできる。"Time or start/end times"を[time],"Event indicator"を[status],"Strata"を[x]にして(色が反転した選択された状態にして),"rho"を0のまま,"部分集合の表現"ボックスの中を削除して[OK]ボタンをクリックすると,ログランク検定の結果がアウトプットウィンドウに表示される("rho"を1にすると,Peto-Peto流の一般化ウィルコクソン検定の結果が得られる)。
EZRでは,これも「統計解析」「生存期間の解析」から「生存曲線の記述と群間の比較(ログランク検定)」を選べば実行できる。
コックス回帰も簡単に説明しておく。カプラン=マイヤ推定やログランク検定は,まったく母数の分布を仮定しない方法だった。コックス回帰は,「比例ハザード性」を仮定するため,比例ハザードモデルと呼ばれる。コックス回帰の基本的な考え方は,イベント発生に影響する共変量ベクトルzi = (zi1, zi2, ..., zip)をもつ個体iの,時点tにおける瞬間イベント発生率h(zi, t)(これをハザード関数と呼ぶ)として,
h(zi, t) = h0(t) ⋅ exp (β1zi1 + β2zi2 + ... + βpzip)
を想定するものである。h0(t)は基準ハザード関数と呼ばれ,すべての共変量のイベント発生への影響がゼロである「基準人」の,時点tにおける瞬間イベント発生率を意味する。β1, β2, ..., βpが推定すべき未知パラメータであり,共変量がexp (βxzix)という比例定数の形でイベント発生に影響するので,このことを「比例ハザード性」と呼ぶのである。なお,Coxが立てたオリジナルのモデルでは,ziが時間とともに変わる,時間依存性共変量の場合も考慮されていたが,現在,通常行われるコックス回帰では,共変量の影響は時間に依存しないもの(時間が経過しても増えたり減ったりせず一定)として扱うことが多い。そのため,個体間のハザード比は時点によらず一定になるという特徴をもつ。つまり,個体1と個体2で時点tのハザードの比をとると,基準ハザード関数h0(t)が分母分子からキャンセルされるので,ハザード比は常に,
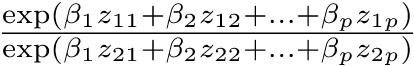
となる。このため,比例ハザード性を仮定できれば,基準ハザード関数の形について(つまり,生存時間分布について)特定のパラメトリックモデルを仮定する必要がなくなる。この意味で,比例ハザードモデルはセミパラメトリックであるといわれる。
生存関数とハザード関数の関係について整理しておく。Tをイベント発生までの時間を表す非負の確率変数とすると,生存関数S(t)は,T ≥ tとなる確率である。S(0) = 1となることは定義より自明である。ハザード関数h(t)は,ある瞬間tにイベントが発生する確率なので,
 である。累積ハザード関数H(t)は,H(t) = ∫0th(u)du = − log S(t)となり,式変形すると,S(t) = exp ( − H(t))とも書ける。共変量ベクトルがzである個体の累積ハザード関数をH(z, t),生存関数をS(z, t)と書けば,前者については,比例ハザード性が成立していれば, H(z, t) = ∫0th(z, u)du = ∫0th0(u)exp (βz)du = exp (βz)H0(t) が成り立ち,それを代入すると,後者について S(z, t) = exp ( − H(z, t)) = exp { − exp (βz)H0(t)} となる。両辺の対数を取って符号を逆にして再び両辺の対数を取ると,log ( − log S(z, t)) = βz + log H0(t)となる。この式から,共変量で層別して,横軸に生存時間をとり,縦軸に生存関数の対数の符号を逆にしてもう一度対数をとった値をとって散布図を描くと,層間でβzだけ平行移動したグラフが描かれることがわかる。これを二重対数プロットと呼ぶ。逆に考えれば,二重対数プロットを描いてみて,層ごとの散布図が平行になっていなければ,「比例ハザード性」の仮定が満たされないので,コックス回帰は不適切といえる。
である。累積ハザード関数H(t)は,H(t) = ∫0th(u)du = − log S(t)となり,式変形すると,S(t) = exp ( − H(t))とも書ける。共変量ベクトルがzである個体の累積ハザード関数をH(z, t),生存関数をS(z, t)と書けば,前者については,比例ハザード性が成立していれば, H(z, t) = ∫0th(z, u)du = ∫0th0(u)exp (βz)du = exp (βz)H0(t) が成り立ち,それを代入すると,後者について S(z, t) = exp ( − H(z, t)) = exp { − exp (βz)H0(t)} となる。両辺の対数を取って符号を逆にして再び両辺の対数を取ると,log ( − log S(z, t)) = βz + log H0(t)となる。この式から,共変量で層別して,横軸に生存時間をとり,縦軸に生存関数の対数の符号を逆にしてもう一度対数をとった値をとって散布図を描くと,層間でβzだけ平行移動したグラフが描かれることがわかる。これを二重対数プロットと呼ぶ。逆に考えれば,二重対数プロットを描いてみて,層ごとの散布図が平行になっていなければ,「比例ハザード性」の仮定が満たされないので,コックス回帰は不適切といえる。
パラメータβの推定には,部分尤度という考え方が用いられる。時点tにおいて個体iにイベントが発生する確率を,時点tにおいてイベントが1件起こる確率と,時点tでイベントが起きたという条件付きでそれが個体iである確率の積に分解すると,前者は生存時間分布についてパラメトリックなモデルを仮定しないと不明だが,後者はその時点でのリスク集合内の個体のハザードの総和を分母,個体iのハザードを分子として推定できる。すべてのイベント発生について,後者の確率だけをかけあわせた結果をLとおくと,Lは,全体の尤度から時点に関する尤度を除いたものになり,その意味で部分尤度あるいは偏尤度と呼ばれる。サンプルサイズを大きくすると真の値に収束し,分布が正規分布で近似でき,分散もその推定量としては最小になるという意味での,「良い」推定量として,パラメータβを推定するには,この部分尤度Lを最大にするようなパラメータを得ればよいことをCoxが予想したので(後にマルチンゲール理論によって証明された),比例ハザードモデルをコックス回帰という(なお,同時に発生したイベントが2つ以上ある場合は,その扱い方によって,Exact法とか,Breslow法,Efron法,離散法などがあるが,可能な場合はExact法を常に使うべきである。また,離散法は,離散ロジスティックモデルに対応する推定法となっていて,生存時間が連続量でなく,離散的にしか得られていない場合に適切である。Breslow法を使う統計ソフトが多いが,Rのcoxph()関数のデフォルトはEfron法である。Breslow法よりもEfron法の方がExact法に近い結果となる)。Rでのコックス回帰の基本は,coxph(Surv(time, cens)~grp+covar, data=dat)という形になる。
例題
leukemiaデータで維持の有無が生存時間に与える影響をコックス回帰せよ。
> require(survival)
> summary(res <- coxph(Surv(time,status)~x, data=leukemia))
> KM <- survfit(Surv(time,status)~x, data=leukemia)
> par(family="sans",las=1,mfrow=c(1,3))
> plot(KM, lty=1:2, main="leukemiaデータのカプラン=マイヤプロット")
> legend("topright", lty=1:2, legend=c("維持","非維持"))
> plot(survfit(res),
+ main="leukemiaデータで維持の有無を共変量とした\n基準生存曲線と95%信頼区間")
> plot(KM, fun=function(y) {log(-log(y))}, lty=1:2,
+ main="leukemiaデータの二重対数プロット")2行目で得られる結果は,下枠内の通りである。
Call:
coxph(formula = Surv(time, status) ~ x, data = leukemia)
n= 23
coef exp(coef) se(coef) z p
xNonmaintained 0.916 2.5 0.512 1.79 0.074
exp(coef) exp(-coef) lower .95 upper .95
xNonmaintained 2.5 0.4 0.916 6.81
Rsquare= 0.137 (max possible= 0.976 )
Likelihood ratio test= 3.38 on 1 df, p=0.0658
Wald test = 3.2 on 1 df, p=0.0737
Score (logrank) test = 3.42 on 1 df, p=0.0645p値が0.074なので,有意水準5%で「維持化学療法の有無が生存時間に与えた効果がない」という帰無仮説は棄却されない(ここで,最下行にScore (logrank) testとあるが,これはRaoのScore検定の結果であり,survdiff()により実行されるログランク検定の結果ではない)。exp(coef)の値2.5が,2群間のハザード比の推定値になるので,維持群に比べて非維持群では2.5倍死亡ハザードが高いと考えられるが,95%信頼区間が1を挟んでおり,有意水準5%では統計学的に有意な違いではない。
3行目以降により,左に2群別々に推定したカプラン=マイヤプロットが描かれ,中央に維持療法の有無を共変量としてコックス回帰したベースラインの生存曲線が描かれ,右に二重対数プロットが描かれる。コックス回帰をした場合のカプラン=マイヤプロットは,中央のグラフのように,比例ハザード性を前提として,群の違いを1つのパラメータに集約させ,生存関数の推定には2つの群の情報を両方用い,共変量の影響も調整して推定したベースラインの生存曲線を95%信頼区間つきで描かせるのが普通である。
どうしても共変量の影響を考えてコックス回帰したベースラインの生存曲線を2群別々に描きたい場合は,coxph()関数の中で,subset=(x=="Maintained")のように指定することによって,群ごとにパラメータ推定をさせることができるが,その場合は独立変数に群分け変数を入れてはいけない。2つ目のグラフを重ねてプロットするときはpar(new=T)をしてから色や線種を変えてプロットすればいいが,信頼区間まで重ね描きすると見にくいのでお薦めしない。
コックス回帰で共変量の影響をコントロールできることの意味をもう少し説明しておく。例えば,がん患者の生存時間を分析するとき,進行度のステージ別の影響は無視できないけれども,これを調整するには,大別して3つの戦略がありうる。
3番目の仮定ができれば,ステージも共変量としてイベント発生への影響を定量的に評価できるメリットがあるが,そのためには,ステージが違ってもベースラインハザード関数が同じでなければならず,やや非現実的である。また,ステージをどのように共変量としてコード化するかによって結果が変わってくる(通常はダミー変数化することが多い)。
2番目の仮定は,ステージによってベースラインハザード関数が異なることを意味する。Rのcoxph()関数で,層によって異なるベースラインハザードを想定したい場合は,strata()を使ってモデルを指定する。例えば,がん患者の生存時間データで,生存時間の変数がtime,打ち切りフラグがstatus,治療方法を示す群分け変数がxであるときに,がんの進行度を表す変数stageがあったとすると,進行度によってベースラインハザード関数が異なることを想定して,治療方法によって生存時間に差が出るかどうかコックス回帰で調べたければ,coxph(Surv(time,status)~x+strata(stage), data=leukemia)とすればよい(但しleukemiaデータにはstageは含まれていないので注意)。
なお,コックス回帰はモデルの当てはめなので,残差分析や尤度比検定,重相関係数の2乗などを用いて,よりよいモデル選択をすることができる。ただし,ベースラインハザード関数の型に特定の仮定を置かないとAICは計算できない。
Rcmdr+RcmdrPlugin.survivalでのコックス回帰は,統計量>モデルへの適合>Cox regression modelを選ぶ。まず“Time or start/end times”は[time],“Event indicator”は[status],“Strata”と“Clusters”は選択しない(“Strata”を指定すると,上述の通り,その層ごとにベースラインハザードが異なると仮定して推定してしまう)。次に,“Method for Ties”はデフォルトが[Efron]になっているが,[Breslow]や[Exact]も選べる。“Robust Standard Errors”は[Default],[Yes],[No]から選べる。“変数”としてハザード比を求めたいグループ変数や共変量を+でつないで指定するが,leukemiaデータでは“x [因子]”しか候補がないので,それをクリックすると,~の右側のボックスには[x]と入る。“部分集合の表現”の下のボックスの中を削除してから [OK]をクリックすれば,コックス回帰の結果が得られる。
EZRでは,統計解析>生存時間の解析>生存時間に対する多変量解析(Cox比例ハザード回帰)を選んで表示されるウィンドウで,変数(ダブルクリックして式に入れる)の枠にある変数名で,[time],[status],[x[因子]]と順にダブルクリックすれば,モデル式:の下の枠の「時間」のところに[time],「イベント」のところに[status],「説明変数」のところに[x]が入る。これで[OK]をクリックすればコックス回帰が実行できるが,[OK]をクリックする前に,「比例ハザード性の分析を行う」の左のボックスをチェックしておけばcox.zph()による比例ハザード性の仮定が満たされているかどうかの検定と図示もやってくれるし115,「ベースラインの生存曲線を示す」の左のボックスをチェックしておけばベースラインの生存曲線と共変量の影響を調整した95%信頼区間が描かれる。
参考
https://minato.sip21c.org/swtips/surv.txtは,Bull and Spiegelhalter (1997)116で生存時間解析の練習用に公開されているデータ(先天性心疾患である肺動脈閉鎖症の患者218人のデータから30人を抜き出したもの)をRで読み込みやすいように,欠損値をNAに変えて(元々は − 1)タブ区切りテキスト形式で保存したものである。
大雑把な日本語解説とRコードをhttps://minato.sip21c.org/swtips/survival.htmlで公開しているので,そこに掲載されている変数の説明やRによる解析方法を参照しながら試行錯誤すれば,生存時間解析の方法が身につくであろう。
変数名とその説明だけ採録しておく。
| 変数名 | 説明 |
|---|---|
agepres | 来院時日齢 |
agelast | 生存していれば最終来院時日齢,死亡した場合は死亡時日齢 |
ageopl | 最初に手術した日齢(未手術なら欠損) |
dead | 生存なら0,死亡していたら1 |
sex | 男性が0,女性が1 |
paanat | 来院時心膜内肺動脈が存在しないか小さければ0,正常かほぼ正常なら1 |
adfol | 適切な追跡かどうか。来院から1年以内に追跡終了したら0,1年以上追跡していたら1 |
followup | 追跡日数(agelast - agepres) |
opfpres | 来院から最初の手術までの間隔(日)(未手術なら欠損) |
unopage | 最初の手術までの追跡日数。手術した人はageopl - agepres,未手術ならlastage - agepres |
unopfpre | 来院から最初の手術または最終来院時までの間隔(手術を受けた人にはopfpresと同じ) |
preopded | 手術前に死亡していたら1,生存していたら0 |
hadop | 手術を受けていれば1,未手術なら0 |
dedlyrpp | 来院から1年以内に死亡していたら1,生存していたら0,適用できなければ2(adfolが0の人) |
agepresx | 来院時日齢のカテゴリ:365日未満なら0,365日以上なら1 |
参考2
Kartsonaki C (2016) Mini-Symposium: Medical Statistics: Survival analysis. Diagnostic Histopathology, 22(7): 263-270. https://doi.org/10.1016/j.mpdhp.2016.06.005も,コンパクトにまとめられた生存時間解析の説明になっている。
この説明では,survivalパッケージに入っているcolonという929人の大腸がん患者のデータが使われているので,EZRでも同じデータを使った解析ができる。
https://minato.sip21c.org/grad/worldfactbook2011.txtは,米国CIAのwebサイトでzip形式に圧縮して公開されている「The world factbook 2011」117から作ったタブ区切りテキスト形式のデータである。
このデータに含まれている変数は,次の通りである。
近年,社会疫学という研究分野において,健康が社会のありようによって影響を受けることが指摘されており,ゼロ歳平均余命や乳児死亡率といった健康指標が,所得の不平等度や国内総生産といった社会経済因子から受ける影響を調べることも行われている。このデータをその視点で統計解析せよ。
図示や記述統計を必ず実行してデータの性状を把握し,検討すべき作業仮説を立て,その仮説を検討するのに適した分析方法を選択し,結果を明記した上で健康指標と社会経済因子の関係について考察を展開すること。