群馬大学 | 医学部 | サイトトップ | 医学情報処理演習
http://phi.med.gunma-u.ac.jp/medstat/p05-2008.txtは,総務省の国勢調査結果から作成した,全国の市の平成12年国勢調査から平成17年国勢調査の間の人口増加率(変数名はH12H17R)のデータである。この人口増加率データが正規分布しているかどうか検定し,結果を考察せよ。なお,検定の有意水準は5%とする。学籍番号・氏名とともに,下のフォームにRのコードと考察を貼り付けて送信すること。
(注)なお,帰無仮説にデータが一致しすぎている場合もあって,そういう場合は捏造あるいは都合のいいデータだけを使った可能性を疑うべきである。有名な例はメンデルのエンドウマメであり,偶然のばらつきもあるはずなのに,それが極端に少なく,データが分離の法則に一致しすぎていたとフィッシャーが指摘している。他の例としては,第二水俣病発覚当時,昭和電工が出してきた上流域住民の毛髪中水銀濃度の分布が,対照地域の住民の毛髪中水銀濃度の分布と一致しすぎていたことが挙げられる。水銀汚染がないといいたいがために,差がなさ過ぎるデータを作ってしまったのであろうと言われている(出典:田栗正章・藤越康祝・柳井晴夫・C.R.ラオ『やさしい統計入門』講談社ブルーバックス)。
dat <- read.delim("http://phi.med.gunma-u.ac.jp/medstat/p05-2008.txt")
layout(1:2)
hist(dat$H12H17R)
qqnorm(dat$H12H17R)
qqline(dat$H12H17R,col="red",lty=2)
shapiro.test(dat$H12H17R)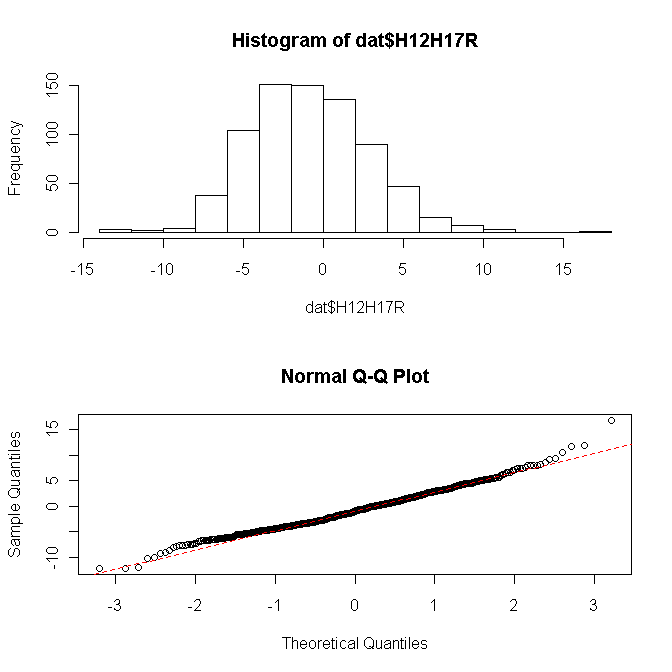
ヒストグラムや正規確率プロットをみると,正規分布にかなり近いが,両端でずれが見られる。Shapiro-Wilkの検定の結果は
W = 0.989, p-value = 2.037e-05
となるので(注:Rの結果の表示で2.037e-05はコンピュータの浮動小数点表示であり,意味は2.037×10-5,つまり0.00002037であって,0.05よりはずっと小さい),データの分布と正規分布に差がないという帰無仮説は有意水準5%で棄却される。つまり,全国の市の人口増加率の分布は正規分布と統計学的に有意な差があるといえる。
Gearyの検定を使うと以下の結果が得られ,差は有意ではない。このことはShapiro-Wilkの検定で有意差があったことと矛盾しない。なぜなら,Gearyの検定は分布の尖り具合が正規分布のそれと一致しているという帰無仮説の検定であり,これが棄却されないことは積極的な正規分布との一致を意味するわけではなく,あくまで尖り具合に差がないという仮説の下で偶然このデータが得られてもおかしくないと言っているだけだからである。実際,先の作図をみると,分布の中央付近ではデータと正規分布がほとんど重なっていて,両端で大きくずれていることがわかる。
> geary.test <- function(X) {
+ m.X <- mean(X)
+ l.X <- length(X)
+ G <- sum(abs(X-m.X))/sqrt(l.X*sum((X-m.X)^2))
+ p <- (1-pnorm((G-sqrt(2/pi))/sqrt(1-3/pi)*sqrt(l.X)))*2
+ cat("Geary's test for normality: G=",G," / p=",p,"\n")
+ }
> geary.test(dat$H12H17R)
Geary's test for normality: G= 0.7992586 / p= 0.8592207