群馬大学 | 医学部 | サイトトップ | 医学情報処理演習
p08-2008.txtは,ある途上国の男性において血液検査をした結果の,ヘモグロビン濃度(変数名hb,単位g/dL),血清鉄濃度(変数名iron,単位mg/L),血清総タンパク濃度(変数名protein,単位g/dL)からなるデータである。ヘモグロビン濃度と血清鉄濃度の相関について検討せよ。できれば,ヘモグロビン濃度が正常値(13 g/dL以上)の人だけのサブセットについても検討し,全体についての結果と比較して考察すること。
学籍番号・氏名とともに(注:絶対に忘れないこと!),下のフォームにRのコードと考察を貼り付けて送信せよ。
library(car)
dat <- read.delim("http://phi.med.gunma-u.ac.jp/medstat/p08-2008.txt")
layout(matrix(1:4,2,2))
attach(dat)
plot(iron,hb,main="ヘモグロビンと血清鉄の関係(全データ)")
data.ellipse(iron,hb,levels=0.8,xlim=c(0,2.5),ylim=c(5,20),
main="ヘモグロビンと血清鉄の関係(全データ)")
cor.test(iron,hb) # (1)
cor.test(iron,hb,method="spearman") # (2)
cor.test(iron,hb,method="kendall") # (3)
detach(dat)
normalhb <- subset(dat,hb>=13)
attach(normalhb)
plot(iron,hb,main="ヘモグロビンと血清鉄の関係(貧血でない人)")
data.ellipse(iron,hb,levels=0.8,xlim=c(0,3),ylim=c(5,20),
main="ヘモグロビンと血清鉄の関係(貧血でない人)")
cor.test(iron,hb) # (4)
cor.test(iron,hb,method="spearman") # (5)
cor.test(iron,hb,method="kendall") # (6)
detach(normalhb)上記コードを実行すると,以下の出力が得られる。
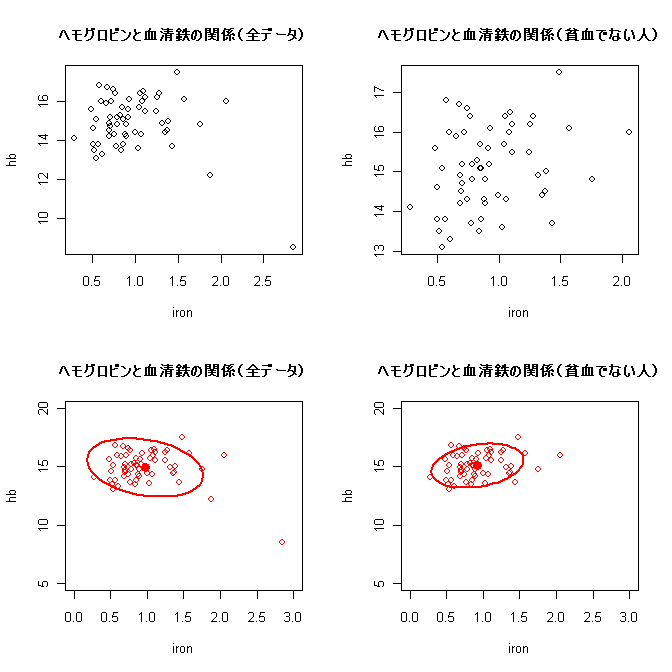
左側の2つのグラフが全員のデータ,右側の2つのグラフがsubset()関数によってヘモグロビン正常値(13 g/dL以上)の人だけからなる部分集団のデータフレームnormalhbについて,ヘモグロビンと血清鉄の関係を見るために描いた散布図である。全員のデータを使った図をみると,全体として負の相関関係があるようにみえるが,右下,つまりヘモグロビン低値で血清鉄高値の人の値が外れ値として全体の関係を歪めているようにもみえる。
(1)により全データを使った場合のピアソンの積率相関係数の推定値と95%信頼区間,相関係数の母数がゼロと差がないという帰無仮説の検定結果が得られる。
Pearson's product-moment correlation
data: iron and hb
t = -2.1374, df = 58, p-value = 0.03680
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.49048164 -0.01748543
sample estimates:
cor
-0.2702104これを見ると,相関係数の点推定量が-0.27と弱い負の相関を示している。有意確率(p-value)が0.037で0.05より小さいので,相関がないという帰無仮説は棄却され,この相関関係は統計的に有意である。
しかし,明らかに右下に外れ値があるので,ピアソンの相関係数はその影響を強く受けてしまい,適切でない可能性がある。そこで順位相関係数を求めてみる。(2)により以下が得られる。同順位があるので正確な有意確率を計算できないという警告メッセージが出ているが仕方ない。
Spearman's rank correlation rho
data: iron and hb
S = 30998.88, p-value = 0.2906
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
0.1386808
Warning message:
In cor.test.default(iron, hb, method = "spearman") :
Cannot compute exact p-values with ties(3)により以下が得られる。
Kendall's rank correlation tau
data: iron and hb
z = 1.1426, p-value = 0.2532
alternative hypothesis: true tau is not equal to 0
sample estimates:
tau
0.1021449(2),(3)のどちらにおいても,順位相関係数がゼロという帰無仮説の検定の有意確率は0.25を超えており,棄却されない。(1)(2)(3)の結果を合わせて考えるとわかることは,どうやらピアソンの積率相関係数として得られた-0.27という値は見かけの相関を示すものに過ぎない可能性が高いということである。
そこでヘモグロビン正常値の人だけの部分集団normalhbを作り,ヘモグロビンと鉄濃度の相関係数について検討しなおしてみる。
すると,まず(4)により以下が得られる。
data: iron and hb
t = 2.0772, df = 56, p-value = 0.04238
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.00984627 0.49178312
sample estimates:
cor
0.2674618ピアソンの相関係数は0.267と弱いが正の相関を示す。相関係数がゼロという帰無仮説の検定の有意確率も0.042と有意である。スピアマンの順位相関係数を計算するため,(5)により以下が得られる。順位相関係数の点推定量は0.258でピアソンの相関係数とほぼ同じである。ただし有意確率が0.05059と5%水準ではわずかに有意ではない。
Spearman's rank correlation rho
data: iron and hb
S = 24123.19, p-value = 0.05059
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
0.2579534(6)によりケンドールの順位相関係数が以下の通り得られる。点推定量は0.180と低めだが,有意確率は0.04838と5%水準で有意であった。即ち,ヘモグロビン濃度と血清鉄濃度の間には,弱いが統計学的に有意な正の相関がある可能性が高い。
Kendall's rank correlation tau
data: iron and hb
z = 1.974, p-value = 0.04838
alternative hypothesis: true tau is not equal to 0
sample estimates:
tau
0.1797718全体では負の相関があったのに,貧血の人を外れ値として除いたら正の相関になったということは,貧血の人が負の相関に寄与するような外れ値となっていたことを意味する。実はこの人たちはマラリアに罹って溶血性貧血を起こしている可能性が高く,赤血球中から血清に出てきたヘモグロビンが分解されて,血清鉄が異常な高値をとってしまって,ヘモグロビンと血清鉄の関係が歪み,見かけ上負の相関関係を示したと考えられる。その人たちを除いて解析し直すと,弱いが有意な正の相関があることがわかり,予想通りであった。