医学情報処理演習第13回「生存時間解析」課題の解答例

2009年2月2日

課題

p13-2008.txtは，1年間の調査期間があったとして，100日目まで参加受付をして，その後風邪を引くかどうかを観察したと仮定した，架空の生存時間データである。変数PIDがID番号，STARTが観察開始日，ENDが観察終了日，TYPEが観察終了の型（0が風邪を引かないまま観察最終日に達したか，あるいは調査期間が終了する前になんらかの理由で調査対象から外れてしまったことを示し，1が風邪を引いたことを示すとする）である。

このデータを読み込み，survivalライブラリを有効にしてから，観察開始から風邪を引くまでの日数を生存時間オブジェクトTIMEに付値するコードは下の枠内の通りである。コードを追加して，TIMEをカプラン＝マイヤ法によって分析し，生存曲線を描き，対象者が風邪を引くまでの日数の中央値（カプラン＝マイヤ推定量）を求めよ。

学籍番号・氏名とともに（注：絶対に忘れないこと！），下のフォームに適切なRのコードと出力結果（生存曲線以外）及び考察を貼り付けて送信せよ。

解答例

必要な関数を追加したRのコードは，以下のようになる。

library(survival)
dat <- read.delim("http://phi.med.gunma-u.ac.jp/medstat/p13-2008.txt")
TIME <- Surv(dat$END-dat$START,dat$TYPE)
res <- survfit(TIME)
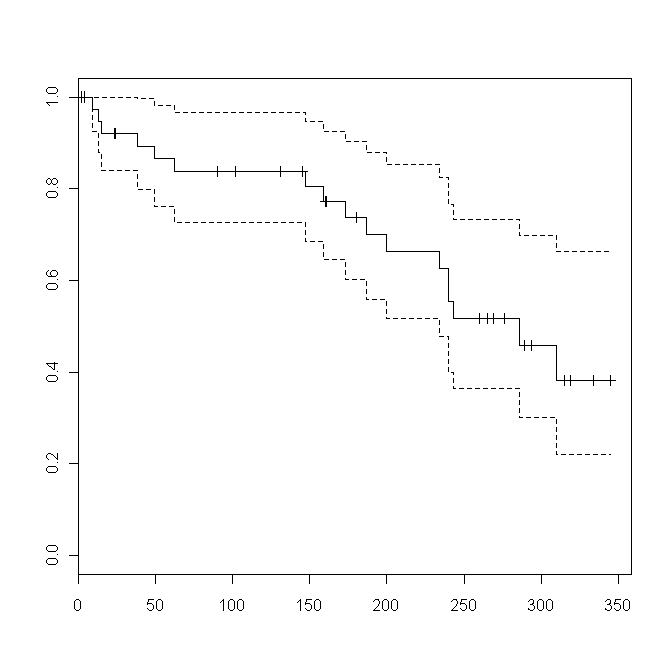
plot(res)
print(res)

出力結果は以下の通り。medianの値が286なので，このデータから風邪を引くまでの時間の中央値は286日（95％信頼区間は234日から無限大）とわかる。

Call: survfit(formula = TIME)

      n  events  median 0.95LCL 0.95UCL 
     40      17     286     234     Inf