群馬大学 | 医学部 | サイトトップ | 医学情報処理演習
survivalライブラリに入っているデータovarianは,卵巣がんに対する2種類の治療法を比較する無作為化臨床試験の結果である。Eastern Cooperative Oncology Groupの研究であり,含まれている変数は以下の通りである。
- futime
- 生存時間または観察打ち切りまでの時間
- fustat
- 打ち切りフラグ
- age
- 年齢
- resid.ds
- 残留疾病の有無(1がなし,2があり)
- rx
- 治療種類(処理群別を示す変数)
- ecog.ps
- ECOG能力状況(0が病気がないのとまったく同じく何の制限もなく活動できる,1が強い運動はできないが軽い家事労働やオフィスワークならできる,2が起きている時間の半分くらいは活動できる,3が半分以上ベッドか椅子にいる,4がセルフケア不能,5が死亡を意味する)
このデータから,治療種類の違いによって卵巣がんの生存時間に差が出たか,年齢を共変量として調整して分析せよ。
プログラムは下記の通り。
require(survival)
data(ovarian)
res <- coxph(Surv(futime,fustat)~age+rx,data=ovarian)
summary(res)
png("it13kadai.png",width=300,height=360)
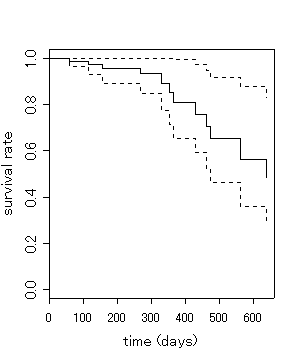
plot(survfit(res),xlab="time (days)",ylab="survival rate")
dev.off()
結果として,下記の出力と,右図が得られる。
Call:
coxph(formula = Surv(futime, fustat) ~ age + rx, data = ovarian)
n= 26
coef exp(coef) se(coef) z p
age 0.147 1.159 0.0461 3.19 0.0014
rx -0.804 0.448 0.6320 -1.27 0.2000
exp(coef) exp(-coef) lower .95 upper .95
age 1.159 0.863 1.059 1.27
rx 0.448 2.234 0.130 1.54
Rsquare= 0.457 (max possible= 0.932 )
Likelihood ratio test= 15.9 on 2 df, p=0.000355
Wald test = 13.5 on 2 df, p=0.00119
Score (logrank) test = 18.6 on 2 df, p=9.34e-05
この結果から,まずLikelihood ratio testの結果をみると,p=0.000355とゼロに近いので,このモデルはデータに適合しているといえる。Rsquareの値から,このモデル,即ち年齢(age)と治療種類(rx)を独立変数とするコックス回帰によって,生存時間の約46%が説明されると考えられる。
次に各独立変数の効果の有意性をみると,年齢(age)は共変量として5%水準で有意に影響している(ので調整するのは正しい)が,治療種類(rx)についてはexp(coef)の95%信頼区間が1を跨いでいるので,治療種類間で生存時間に有意な差はないと考えられる。