群馬大学 | 医学部 | サイトトップ | 医学情報処理演習
2009年12月8日
これまでの課題と同じく,sample02.txtを用いる。
変数SEXは性別を示し,"M"が男性,"F"が女性を意味する。変数BMIはBody Mass Indexを示し,肥満度の指標となる。SBPは収縮期血圧(mmHg)を意味する。これら3つの変数を用いて,男女別に,BMIとSBPの相関関係があるかどうか検討せよ。
なお,検定の有意水準は5%とし,検定を実行する前に図示もして,図と検定結果を参照して考察を書くものとする。学籍番号・氏名とともに,下のフォームにRのコードと考察を貼り付けて送信すること。
必要な解析を行うコードを次の枠内に示す。
dat <- read.delim("http://phi.med.gunma-u.ac.jp/medstat/sample02.txt")
males <- subset(dat,SEX=="M") # 男性だけのデータ
females <- subset(dat,SEX=="F") # 女性だけのデータ
library(car) # carライブラリを呼び出す
png("it2009-08.png",width=640,height=320) # png形式画像ファイルを開く
layout(t(1:2)) # 画面を横に2分割
data.ellipse(males$BMI,males$SBP,levels=0.8,main="男性のBMIと収縮期血圧の関係と\n80%集中楕円")
data.ellipse(females$BMI,females$SBP,levels=0.8,main="女性のBMIと収縮期血圧の関係と\n80%集中楕円")
dev.off() # pngファイルを閉じる
cor.test(males$BMI,males$SBP)
cor.test(females$BMI,females$SBP)これを実行すると,次のグラフができる。男性の方が楕円が真円に近いので,女性よりもBMIと収縮期血圧の関係は弱そうである。
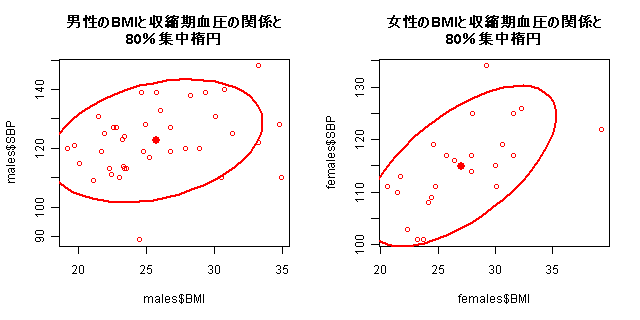
下から2行目のコードで,男性についてピアソンの相関係数を95%信頼区間とともに求め,母相関係数がゼロという帰無仮説の検定を行っている。結果は次の通り。p-valueが0.06307と5%より大きいので,有意水準5%で帰無仮説は棄却されず,相関は有意でない。
Pearson's product-moment correlation
data: males$BMI and males$SBP
t = 1.918, df = 36, p-value = 0.06307
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
-0.01683502 0.56880340
sample estimates:
cor
0.3044870 コードの最後の行で女性について同様に計算した結果は,次のようになる。p-valueは0.001227と5%より小さいので,母相関係数がゼロという帰無仮説は棄却され,有意な相関があるといえる。ピアソンの相関係数は,0.63(95%信頼区間は[0.29, 0.83])なので,絶対値0.2〜0.4が弱い相関,0.4〜0.7が中等度の相関,0.7〜1が強い相関という目安に従えば,中等度の正の相関があるといえる。
Pearson's product-moment correlation
data: females$BMI and females$SBP
t = 3.7334, df = 21, p-value = 0.001227
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.2966533 0.8281970
sample estimates:
cor
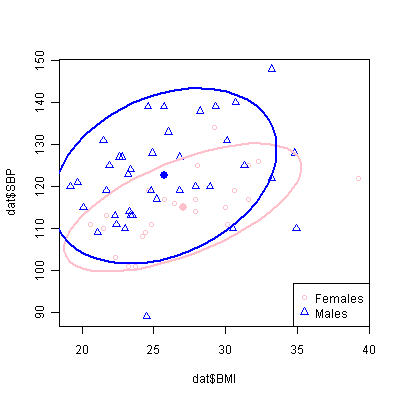
0.6316202 上の解答例では,先に男女を分けてしまったが,もちろん,プロットは男女を1つのグラフにして記号で塗り分けておき,相関係数の計算をするときに分けることも可能である。例えば下記。
dat <- read.delim("http://phi.med.gunma-u.ac.jp/medstat/sample02.txt")
library(car)
png("it2009-08a.png", width=400, height=400)
plot(dat$BMI,dat$SBP,pch=as.integer(dat$SEX),col=c("pink","blue")[as.integer(dat$SEX)])
data.ellipse(dat$BMI[dat$SEX=="F"],dat$SBP[dat$SEX=="F"],plot.points=F,levels=0.8,col="pink")
data.ellipse(dat$BMI[dat$SEX=="M"],dat$SBP[dat$SEX=="M"],plot.points=F,levels=0.8,col="blue")
legend("bottomright",pch=1:2,col=c("pink","blue"),c("Females","Males"))
dev.off()
cor.test(dat$BMI[dat$SEX=="F"],dat$SBP[dat$SEX=="F"])
cor.test(dat$BMI[dat$SEX=="M"],dat$SBP[dat$SEX=="M"])描かれる図は次のようになる。しかしこのデータでは,男女別々の図の方が見やすいであろう。cor.test()の結果は上の解答例とまったく同じになる。