群馬大学 | 医学部 | サイトトップ | 医学情報処理演習
2009年12月16日
これまでの課題と同じく,sample02.txtを用いる。下のフォームに最初から書かれているコードは,データを読み込んで,男性の人数をMalesTotalという変数に付値し,男性のうち「ほぼ毎日」蚊帳を使っている人数をMalesNetUserという変数に付値するコードである。ここで,変数SEXは性別を示し,"M"が男性,"F"が女性を意味する。変数BEDNETは蚊帳の使い方を示し,1が「ほぼ毎日」,2が「時々」,3が「ほとんど使わない」,4が「持っていない」を意味する。
必要なコードを追加し,男女間で,蚊帳を「ほぼ毎日使う」割合に差があるか検定せよ(2群間の比率の差の検定)。検定の有意水準は5%とし,検定を実行する前に図示もして,図と検定結果を参照して考察を書くものとする。学籍番号・氏名とともに,下のフォームにRのコードと考察を貼り付けて送信すること。
コードを以下に示す。
dat <- read.delim("http://phi.med.gunma-u.ac.jp/medstat/sample02.txt")
MalesTotal <- sum(dat$SEX=="M")
MalesNetUser <- sum(dat$BEDNET[dat$SEX=="M"]==1)
FemalesTotal <- sum(dat$SEX=="F")
FemalesNetUser <- sum(dat$BEDNET[dat$SEX=="F"]==1)
(NetUser <- c(MalesNetUser,FemalesNetUser))
(Total <- c(MalesTotal,FemalesTotal))
names(Total) <- c("Males","Females")
prop.test(NetUser,Total)
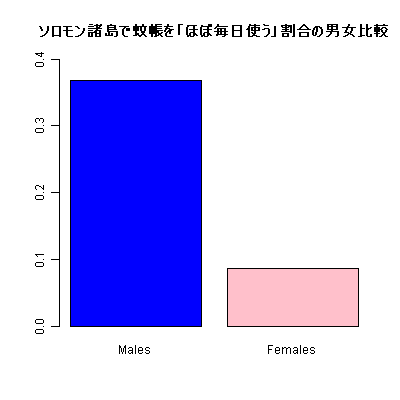
barplot(NetUser/Total,main="ソロモン諸島で蚊帳を「ほぼ毎日使う」割合の男女比較", col=c("blue","pink"),ylim=c(0,0.4))次の図が描かれ,枠内の結果が得られる。
2-sample test for equality of proportions with continuity correction
data: NetUser out of Total
X-squared = 4.5017, df = 1, p-value = 0.03386
alternative hypothesis: two.sided
95 percent confidence interval:
0.05477823 0.50815084
sample estimates:
prop 1 prop 2
0.36842105 0.08695652 蚊帳を「ほぼ毎日使う」割合は,男性で約37%女性で8.7%であり,その差の95%信頼区間は5.5ポイントから51ポイントであることがわかる。有意確率が0.03386なので,男女間で蚊帳を「ほぼ毎日使う」割合に差がないという帰無仮説は有意水準5%で棄却され,男女間で統計学的に有意な差があるといえる。
実は,"=="とsum()関数を使うよりも,カテゴリ別の人数を求めるにはtable()関数を使う方が遥かに簡単である。table()を使う場合のコードは以下の通り。
dat <- read.delim("http://phi.med.gunma-u.ac.jp/medstat/sample02.txt")
Total <- table(dat$SEX)
NetUser <- table(dat$SEX[dat$BEDNET==1])
prop.test(NetUser,Total)
barplot(NetUser/Total,main="ソロモン諸島で蚊帳を「ほぼ毎日使う」割合の男女比較", col=c("blue","pink"),ylim=c(0,0.4))