群馬大学 | 医学部 | サイトトップ | 医学情報処理演習
2010年2月9日
pcancer.txtは,大橋,浜田(1995) の付録A.3に掲載されている膵臓癌データを入力してタブ区切りテキストファイルとして公開してあるものである。以下は,このデータを読み込んでデータの型などを設定し,生存時間分析ライブラリsurvivalをロードしてから,survfit()関数でカプラン=マイヤ法により観察打ち切りを考慮しつつ術中放射線照射の有無別に生存曲線の推定を行い,最後にログランク検定により術中放射線照射の有無により生存時間に差はでないという帰無仮説を検定するRのプログラムである。
dat <- read.delim("http://phi.med.gunma-u.ac.jp/medstat/pcancer.txt")
dat$CENSOR <- 1-dat$CENSOR
dat$SEX <- factor(dat$SEX, labels=c("男性(Males)","女性(Females)"))
dat$TREAT <- factor(dat$TREAT, labels=c("照射なし(without irradiation)","照射あり(with irradiation)"))
dat$CH <- ordered(dat$CH,labels=c("CH0","CH1","CH2","CH3"))
dat$STAGE <- ordered(dat$STAGE,labels=c("III","IV"))
dat$PS <- ordered(dat$PS,labels=c("0,1","2","3","4"))
# data from 大橋・浜田(1995)「生存時間解析 SAS による生物統計」東京大学出版会付録A.3
# 膵臓がんデータ(Nishimura et al. 1988. の一部)
# 手術中放射線照射の延命効果をみる目的のデータだがランダム割付ではない。
# 入力 Minato Nakazawa 20/1/2007 * R では死亡が1 なのでCENSOR のカテゴリに注意。
# *** 変数リスト***
# CASENO 患者番号 (Number of patient)
# TIME 生存時間(月) 連続量 (Survival time in months)
# CENSOR 打ち切りの有無を示すフラグ
# (元データでは打ち切りが1,死亡が0 でR と逆なので1 から引く)
# (The flag indicates the record being censored (0) or not (1))
# (* Original data takes opposite coding, so subtracting from 1 in this code)
# AGE 手術時の年齢 連続量 (Age at operation)
# SEX 性別 0 が男性,1 が女性 (Sex, 0 is male, 1 is female)
# TREAT 処置法 0 が術中照射無し,1 が術中照射あり
# (Treatment, 0 without irradiation during operation, 1 with it)
# BUI 占拠部位 0 が頭部,1 が頭部以外
# (Occupied area, 0 head. 1 other)
# CH 膵内胆管への浸潤 順序尺度 1:CH0,2:CH1,3:CH2,4:CH3
# (extent of invasion into intrapancreas bile tract)
# P 腹膜播種性転移 0 がなし,1 があり
# (metastasis spreading over peritoneum, 0: no, 1: exist)
# STAGE TNM 分類のステージ 順序尺度 3:III 期,4:IV 期
# (stage of TNM criteria)
# PS Performance Status(活動度) 順序尺度 1:0,1,2:2,3:3,4:4
library(survival)
print(KM <- survfit(Surv(dat$TIME,dat$CENSOR) ~ dat$TREAT))
plot(KM, lty=1:2)
legend("topright",lty=1:2,legend=levels(dat$TREAT))
survdiff(Surv(dat$TIME,dat$CENSOR) ~ dat$TREAT)このコードをRで実行し,下のフォームに,学籍番号・氏名とともに出力結果の解釈を記入して送信せよ。なお,検定の有意水準は5%とする。
pcancer.txt is a tab-separated text file, based on the pancreas cancer data (cited from Appendix A.3 of the book "Survival Analysis: Biostatistics using SAS", Ohashi Y, Hamada C, 1995, University of Tokyo Press). The program listed above is to read this data file, to set the type of variables, to load survival library, to estimate survival curves by whether irradiation during operation was conducted or not, compare Kaplan-Meier estimate with considering censoring data, and to test the null-hypothesis of "There is no difference of survival times by whether irradiation during operation was conducted or not" by log-rank test.
Discuss the results in the form below (let the significance level of the test 0.05). Never forget to write the student ID and name in each field.
出力結果は,次の図と表である。
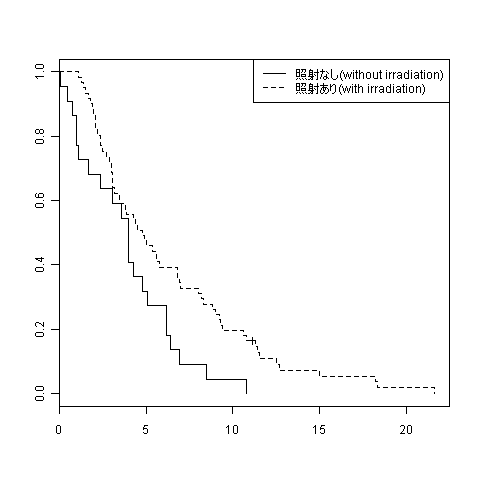
Call: survfit(formula = Surv(dat$TIME, dat$CENSOR) ~ dat$TREAT) records n.max n.start events median dat$TREAT=照射なし(without irradiation) 22 22 22 22 4.0 dat$TREAT=照射あり(with irradiation) 61 61 61 60 4.8 0.95LCL 0.95UCL dat$TREAT=照射なし(without irradiation) 2.4 6.2 dat$TREAT=照射あり(with irradiation) 3.5 6.9Call: survdiff(formula = Surv(dat$TIME, dat$CENSOR) ~ dat$TREAT) N Observed Expected (O-E)^2/E dat$TREAT=照射なし(without irradiation) 22 22 14.1 4.462 dat$TREAT=照射あり(with irradiation) 61 60 67.9 0.925 (O-E)^2/V dat$TREAT=照射なし(without irradiation) 5.77 dat$TREAT=照射あり(with irradiation) 5.77 Chisq= 5.8 on 1 degrees of freedom, p= 0.0163
カプランマイヤ法により,観察打ち切りを考慮した術中放射線照射あり群の生存時間の中央値は4.8ヶ月(95%信頼区間3.5ヶ月〜6.9ヶ月),術中放射線照射なし群の生存時間の中央値は4.0ヶ月(95%信頼区間2.4ヶ月〜6.2ヶ月)で,あまり差がないようにみえる。これは,生存曲線をみれば,生残確率が50%の辺りで2群の生存曲線が接近しているためであることがわかる。それ以外のところでは,一貫して,術中放射線あり群の方が術中放射線照射なし群よりも生存曲線がかなり上に位置している。
ログランク検定により2群の生存時間に差は無いという帰無仮説を検定すると,カイ二乗値が5.8,有意確率が0.0163となり,有意水準5%で統計学的に有意であり,帰無仮説は棄却される。即ち,2群の間で生存時間には統計学的に有意な差があったといえる。