群馬大学 | 医学部 | サイトトップ | 医学情報処理演習
医学情報処理演習:2010年度第4回課題解答例
課題
テキスト表4-1に示す成人男性100万人の母集団についての身長データは,次のコードで入力できる。Xに100万人の身長データが付値される。
HT <- 144:191 # Set heights into variable HT in cm.
NUM <- c(2,3,6,17,19,56,125,219,463,915,1609,2649,4550,7214,11005,16081,
22098,29903,39048,48312,57703,66639,73332,78051,79829,77866,73767,66321,
57993,48410,39081,29967,22055,15810,10875,7309,4596,2726,1519,939,462,
224,128,50,31,14,5,4) # Set the number of individuals with each height.
X <- rep(HT,NUM) # Make a new variable X as heights for a million people.
次に,ランダムな標本抽出を行うために,まずRNGkind("Mersenne-Twister")によって乱数生成アルゴリズムをメルセンヌツイスター法に指定し(注:乱数については,このページを参照されたい),set.seed(54321)によって乱数を初期化する。このことによって,解答者全員がまったく同じサンプリングを行うことができる。
RNGkind("Mersenne-Twister") # Specify how to make pseudo-random numbers (random number generator; RNG)
set.seed(54321) # Initialize the RNG
なお,ここまでのRコードは,c04enter.Rにも示すので,コピー&ペーストできる。
ここからが問題だが,10人,100人,1000人の非復元抽出を2回ずつ行い,それぞれの平均と不偏標準偏差を,母集団の平均と標準偏差とともに求め,それぞれヒストグラムを描画するコードは,次のようになる。空白に適切な文字列または数字を入れよ。また,結果から何がいえるか考察せよ。
meansdhist <- function(Y, ...) { # Definition of function to draw histogram and calculate mean and sd
![[A]](./box_A.png) (Y, right=FALSE,
(Y, right=FALSE, ![[B]](./box_B.png) =c(140, 200), ...) # draw a histogram, where each interval
=c(140, 200), ...) # draw a histogram, where each interval
# including lower limit and excluding upper limit,
# with ranges between 140 and 200.
RES <- c(mean(Y), sd(Y)) # Calculating mean and sd as a numeric vector, named RES
![[C]](./box_C.png) (RES) <- c("mean","sd") # Naming the two elements of RES
(RES) <- c("mean","sd") # Naming the two elements of RES
return(RES) # Return the vector of mean and sd
}
S10M <- sample(X,10,rep=FALSE) # Randomly sampling 10 from the population X without replacement
S10N <- sample(X,10,rep=FALSE) # Randomly sampling 10 from the population X without replacement
S100M <- sample(X,100,rep=FALSE) # Randomly sampling 100 from the population X without replacement
S100N <- sample(X,100,rep=FALSE) # Randomly sampling 100 from the population X without replacement
S1000M <- sample(X,1000,rep=FALSE) # Randomly sampling 1000 from the population X without replacement
S1000N <- sample(X,1000,rep=FALSE) # Randomly sampling 1000 from the population X without replacement
par(mar=c(4,4,0.5,0.5),cex=0.6)
layout(1:7)
meansdhist(S10M, main="A histogram of randomly sampled 10 values of heights, 1st trial")
meansdhist(S10N, main="A histogram of randomly sampled 10 values of heights, 2nd trial")
meansdhist(S100M, main="A histogram of randomly sampled 100 values of heights, 1st trial")
meansdhist(S100N, main="A histogram of randomly sampled 100 values of heights, 2nd trial")
meansdhist(S1000M, main="A histogram of randomly sampled 1000 values of heights, 1st trial")
meansdhist(S1000N, main="A histogram of randomly sampled 1000 values of heights, 2nd trial")
hist(X, right=FALSE, xlim=c(140, 200), main="The histogram of heights for the population X")
print(EX <- mean(X)) # Mean of X, assigned to EX
sqrt(sum((X-EX)^![[D]](./box_D.png) )/length(X)) # Standard deviation for the population X
)/length(X)) # Standard deviation for the population X
(The program listed above is to enter the heights for one million people (the whole population) as a variable X, to initialize random number generator, and to do several kinds of random sampling with viewing the nature of those samples by calculating means and sds and by drawing histograms. Please fill the boxes from ![[A]](./box_A.png) to
to ![[D]](./box_D.png) and discuss the results.)
and discuss the results.)
解答例
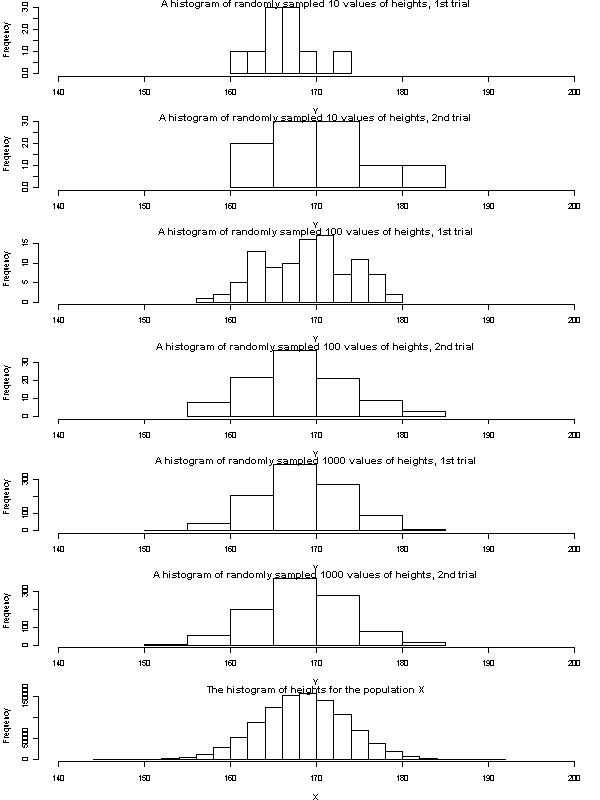
空欄を上の表の通りに正しく埋めて実行すると(なお,演習室のコンピュータでは,それに加えて太字の命令文を追加して描画余白を減らさないと実行できなかったが),右のグラフと下の結果が得られる。
| 変数 | サイズ | 試行順序 | 平均値 | (不偏)標準偏差 |
|---|
| S10M | 10 | 1 | 165.700000 | 3.683296 |
| S10N | 10 | 2 | 169.300000 | 5.812821 |
| S100M | 100 | 1 | 168.460000 | 5.083982 |
| S100N | 100 | 2 | 167.520000 | 5.518527 |
| S1000M | 1000 | 1 | 167.911000 | 4.943027 |
| S1000N | 1000 | 2 | 167.816000 | 5.085273 |
| X | 1000000 | (母集団) | 167.9998 | 5.009512 |
この結果からわかることは,(1)サンプルサイズが大きくなるほど2回の試行結果が似ているように見える,(2)サンプルサイズが大きくなるほど,標本平均は母平均に近づき,不偏標準偏差は母集団の標準偏差に近づくように見える,ということである。
要望・質問
- コードを穴埋めさせる問題の[A]、[B]、[C]...をコード中から探すのが手間なので、文字色を変えるなどをしていただけるとありがたいです。
- 前回のように箱の画像にします
- par(mar=c(4.2,4.1,0.4,0.5))と入力したら図を見ることができました。
- 演習室のコンピュータの画面の解像度が低いことに気付かず,図が出ない状態で課題を出してしまって失礼しました。このパラメータを試行錯誤で見つけたのだと思いますが,脱帽です。
- 課題を解く時間をもう少し長く/コードを示す時間を長く
- 前半丁寧にやりすぎ,時間配分を間違えました。すみません。
- 授業内で使用するRの関数リファレンスを作っていただけると、効率が良くなり、理解が高まると思うのですが、いかがでしょうか?
- これはいいアイディアだと思います。時間があったら用意します。
- EX,VX,SXのあたりの説明がはやくてよくわかりませんでした
- 母集団の平均値,分散,標準偏差を出すところですね。実際に標本調査をしているときは,母集団の真の値は未知なので,こんな計算はできませんが,ここでは,標本抽出と母数推定のメカニズムを調べるために,仮に我々が全知全能で母集団の真の値も全部わかっていたとしたら,という状況を想定してください。EX <- mean(X)として母平均,VX <- sum((X-EX)^2)/length(X)として母分散(母集団統計量を計算するときは不偏分散ではないのでvar(X)ではダメです),SX <- sqrt(VX)として母集団の標準偏差(同じ理由でsd(X)ではダメです)を求めます。母集団の標準偏差がSXだとわかっていれば,例えばサイズ10の標本Zを抽出した場合の,標本平均の標準誤差がSX/sqrt(10)となります。標本調査をする場合は,母集団の標準偏差は未知なので,通常は標本Zの不偏標準偏差sd(Z)を母集団の標準偏差の代わりに使って標準誤差を計算しますが,このようにサンプルサイズが小さすぎる場合は,この代用にはかなり無理があるので,計算された標準誤差と真の標準誤差との間には,かなりの違いが出てしまうことが多いです。
- 真の標準誤差
> sqrt(VX)/sqrt(10)
[1] 1.584147
標本からの誤差?
> sd(Z)/sqrt(10)
[1] 1.164760
ずれている。ってところらへんがよくわかりませんでした。
- 上の説明(とくに下線部)で答えになったでしょうか?
リンクと引用について
![]() (Y, right=FALSE,
(Y, right=FALSE, ![]() =c(140, 200), ...) # draw a histogram, where each interval
=c(140, 200), ...) # draw a histogram, where each interval![]() (RES) <- c("mean","sd") # Naming the two elements of RES
(RES) <- c("mean","sd") # Naming the two elements of RES![]() )/length(X)) # Standard deviation for the population X
)/length(X)) # Standard deviation for the population X