群馬大学 | 医学部 | サイトトップ | 医学情報処理演習
医学情報処理演習:2010年度第5回課題解答例
課題
http://phi.med.gunma-u.ac.jp/medstat/sample02.txtは,ソロモン諸島の首都のとある学校で実施した健診結果を,昨年の実習で入力してもらった後にエラーを訂正したタブ区切りテキスト形式データである。このデータを読み込んで,BMIの値が正規分布しているかどうか男女別に調べ,有意水準を5%として検定するためのコードと出力結果とその解釈を下に示す。学籍番号・氏名とともに,下のフォームと解釈文を穴埋め[Box AとBには適切な関数名を入力し,C〜Fに,その次の( )内から適切な方を選択して数字で入力]して送信せよ。
(Please fill the box A and B by adequate function names, and fill the box C to F by the number 1 or 2, selecting from the following 2 candidates with parenthesis. Here we assume the significance level of statistical test as 0.05.)
まず,下記のコードを実行する。
x <- read.delim("http://phi.med.gunma-u.ac.jp/medstat/sample02.txt") # データをxに読み込む
layout(t(1:2)) # 画面を左右に2分割する
tapply(x$BMI,x$SEX, ) # 男女別にBMIの正規確率プロットを描画する (Draw Q-Q plots by sex)
) # 男女別にBMIの正規確率プロットを描画する (Draw Q-Q plots by sex)
tapply(x$BMI,x$SEX, ) # 男女別にBMIの分布の正規性をShapiro-Wilkの検定 (Do Shapiro-Wilk test by sex)
) # 男女別にBMIの分布の正規性をShapiro-Wilkの検定 (Do Shapiro-Wilk test by sex)
結果として,グラフ描画と同時にプロットに使われた数値も表示されるが,最後にShapiro-Wilkの検定の結果が表示されるので,それを示す。
$F
Shapiro-Wilk normality test
data: X[[1L]]
W = 0.9432, p-value = 0.21
$M
Shapiro-Wilk normality test
data: X[[2L]]
W = 0.938, p-value = 0.03612
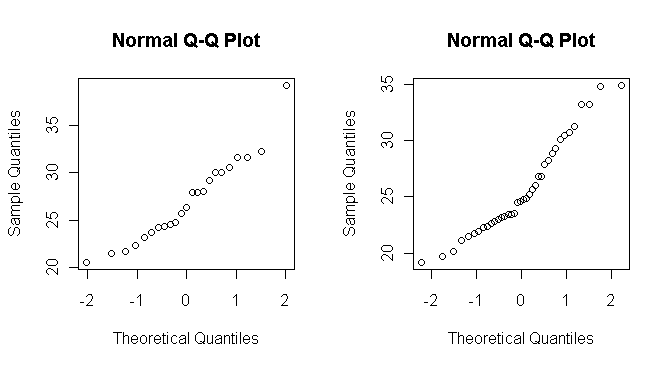
正規確率プロットのグラフは,左が女性,右が男性である。 (1. 女性|2. 男性)のグラフは,1人だけ極端にBMIの高い人がいるが,その人を除けば,正規確率プロットはほぼ直線に乗っている。一方,
(1. 女性|2. 男性)のグラフは,1人だけ極端にBMIの高い人がいるが,その人を除けば,正規確率プロットはほぼ直線に乗っている。一方, (1. 女性|2. 男性)のグラフは,極端な外れ値は見られないが,グラフ全体が直線より下に凸になっており,直線性が低いようにみえる。
(1. 女性|2. 男性)のグラフは,極端な外れ値は見られないが,グラフ全体が直線より下に凸になっており,直線性が低いようにみえる。
(The normal Q-Q plots are shown as females at left, males at right. The graph of  (1. Females | 2. Males) shows almost linear shape except for 1 extremely high BMI individual. On the other hand, The graph of
(1. Females | 2. Males) shows almost linear shape except for 1 extremely high BMI individual. On the other hand, The graph of  (1. Females | 2. Males) shows no extreme outlier, but underslung curve as overall shape.)
(1. Females | 2. Males) shows no extreme outlier, but underslung curve as overall shape.)
Shapiro-Wilkの検定結果をみると,$F,つまり女性の方は,p-valueが0.21であり,有意水準である5%(つまり0.05)より大きいので,「データの分布は正規分布に従う」という帰無仮説は棄却 (1. される|2. されない)。つまり,女性のBMIの分布は正規分布と統計的に有意な差があるとはいえないので,とりあえず正規分布を仮定しても差し支えない。しかし,$M,つまり男性の方は,p-valueが0.03612と有意水準より小さいので,帰無仮説が棄却
(1. される|2. されない)。つまり,女性のBMIの分布は正規分布と統計的に有意な差があるとはいえないので,とりあえず正規分布を仮定しても差し支えない。しかし,$M,つまり男性の方は,p-valueが0.03612と有意水準より小さいので,帰無仮説が棄却 (1. される|2. されない)。つまり,男性のBMIの分布は,有意水準5%で,正規分布と統計学的に有意な差があるといえる。
(1. される|2. されない)。つまり,男性のBMIの分布は,有意水準5%で,正規分布と統計学的に有意な差があるといえる。
(The results of Shapiro-Wilk test suggest: In females indicated by "$F", p-value 0.21 is more than 0.05 (significance level here), so that we  (1. can | 2. cannot) reject the null-hypothesis that the distribution of the data obeys normal distribution. However, in males indicated by "$M", p-value 0.03612 is less than 0.05, so that we
(1. can | 2. cannot) reject the null-hypothesis that the distribution of the data obeys normal distribution. However, in males indicated by "$M", p-value 0.03612 is less than 0.05, so that we  (1. can | 2. cannot) reject the same null-hypothesis. Thus the distribution of males' BMI is significantly different from the normal distribution at 5% level.)
(1. can | 2. cannot) reject the same null-hypothesis. Thus the distribution of males' BMI is significantly different from the normal distribution at 5% level.)
(注)なお,帰無仮説にデータが一致しすぎている場合もあって,そういう場合は捏造あるいは都合のいいデータだけを使った可能性を疑うべきである。有名な例はメンデルのエンドウマメであり,偶然のばらつきもあるはずなのに,それが極端に少なく,データが分離の法則に一致しすぎていたとフィッシャーが指摘している。他の例としては,第二水俣病発覚当時,昭和電工が出してきた上流域住民の毛髪中水銀濃度の分布が,対照地域の住民の毛髪中水銀濃度の分布と一致しすぎていたことが挙げられる。水銀汚染がないといいたいがために,差がなさ過ぎるデータを作ってしまったのであろうと言われている(出典:田栗正章・藤越康祝・柳井晴夫・C.R.ラオ『やさしい統計入門』講談社ブルーバックス)。
解答例
| 項目 | 入力欄 |
|---|
 | qqnorm |
 | shapiro.test |
 | 1 |
 | 2 |
 | 2 |
 | 1 |
なお,「有意」かどうか,帰無仮説が棄却されるかどうか,有意確率(=p-value)が有意水準より小さいかどうかといったことは,帰無仮説が「データが正規分布に従っている(データの分布と正規分布に差がない)」だとすると,次の表の形にまとめることができる。有意水準とは,予め決めておくべき,「もし,この値より有意確率が小さかったら,偶然ではありえないくらい珍しいことが起こっている(から最初の帰無仮説を疑おう)と考える基準値」のことで,5%か1%にする(分野によって,あるいは研究対象によっても異なる)のが普通である。
| 有意確率<有意水準 | 有意確率≧有意水準 |
|---|
| 帰無仮説が棄却される | 帰無仮説は棄却されない |
| データの分布と正規分布には統計学的な有意差がある | データの分布と正規分布には統計学的に有意な差はない |
データは正規分布に従わない
(データの分布は正規分布と異なるという意思決定ができる) | データが正規分布に従っていることは否定されない
(データの分布が正規分布と異なるとは言えない) |
要望・質問
- Adobe Readerのトラブルでpdfファイルが10秒程度しか見られない(開いてから約10秒後にフリーズする)。pc-34,pc-35で確認したが、pc-36は問題ない。他にもいくつか同じ症状が出ているPCが存在する模様/PDFが読めませんでした。PDFを開くと30秒くらいで停止しました。
- 情報メディアセンターに確認をお願いしたところ,概ね以下のような回答でした。
- ・pc-34とpc-35のAdobe Readerは2台とも正常に動作した
- ・pc-34は動作が遅いためPCの交換をする予定
- ・たぶんハードウェアの不調
- ・ログイン後、画面右下に「オフラインファイルは、同期のために今セットアップされます」と出た後、それが消えるまでは、ファイルを開いたりせず、お待ちいただいた方が確実
- 検定はテストにおいても重要ですか? なるべく簡単のがいいです。
- 重要です。簡単なものを出します。
- 後半の進行が早いです
- ペース配分は改善に努力します。
- 使う関数をまとめるのは、大変な作業だと思いますが、実現したら本当に助かるので、先生のご負担にならない範囲でぜひお願いします/授業で使った各関数の意味や使い方をまとめた表を最後にもらえると助かります/授業のポイントや要点をまとめたものを、プリントかオンライン公開してくださると、授業の流れが分かりやすいです。
- 今回に関しては,このページをご覧ください。
リンクと引用について
![]() ) # 男女別にBMIの正規確率プロットを描画する (Draw Q-Q plots by sex)
) # 男女別にBMIの正規確率プロットを描画する (Draw Q-Q plots by sex)![]() ) # 男女別にBMIの分布の正規性をShapiro-Wilkの検定 (Do Shapiro-Wilk test by sex)
) # 男女別にBMIの分布の正規性をShapiro-Wilkの検定 (Do Shapiro-Wilk test by sex)