医学情報処理演習：2011年度第5回課題解答例

第5回に出てきた関数と文の主なものはこちら（2011年11月9日追記：qqnorm()の説明を追加した）を参照されたい。

今回の課題は出題に不備があり，オゾン濃度と風速が混乱していたので，Box AとBox Bのみ解答していただきました。申し訳ありませんでした。以下の課題は不備だった点を修正済みです。

課題

Rに元々含まれている1973年のニューヨーク市の大気環境データairqualityに含まれている変数のうち，ルーズヴェルト島の昼過ぎ２時間の平均オゾン濃度を意味するOzoneとLaGuardia空港の7:00～10:00の平均風速（マイル／時）を意味するWindの値が正規分布しているかどうか月別に調べ，有意水準を5％として検定するためのコードと出力結果とその解釈を下に示す。学籍番号・氏名とともに，下のフォームと解釈文を穴埋めして送信せよ。

(Please fill the boxes. Here we set the significance level of the all statistical tests as 0.05.)

まず，下記のコードを実行する。

attach(airquality) # 組み込みデータフレームairqualityを利用中にする。
windows(width=640,height=768) # 横640ピクセル，縦768ピクセルのグラフィック画面を開く
nM <- length(table(Month)) # airqualityデータフレームに含まれる「月」の数をnMに付値
layout(matrix(1:(2*nM),nc=2)) # 画面を上下にnM分割，左右２分割し，左上から左下，右上から右下の順で描画
tapply(Ozone,Month,,main="Ozone's normal Q-Q plot") # オゾン濃度の正規確率プロットを月別に描画
tapply(Wind,Month,,main="Wind's normal Q-Q plot") # 風速の正規確率プロットを月別に描画
tapply(Ozone,Month,) # オゾン濃度の分布の正規性を月別にShapiro-Wilkの検定
tapply(Wind,Month,) # 風速の分布の正規性を月別にShapiro-Wilkの検定
detach(airquality) # airqualityのattach状態を終了する。

結果として，グラフ描画と同時にプロットに使われた数値も表示されるが，最後にShapiro-Wilkの検定の結果が表示されるので，それを示す。

airquality$Ozoneとairquality$Windの月別正規確率プロット

> tapply(Ozone,Month,shapiro.test)
$`5`

	Shapiro-Wilk normality test

data:  X[[1L]] 
W = 0.714, p-value = 8.294e-06


$`6`

	Shapiro-Wilk normality test

data:  X[[2L]] 
W = 0.8433, p-value = 0.0628


$`7`

	Shapiro-Wilk normality test

data:  X[[3L]] 
W = 0.9797, p-value = 0.8669


$`8`

	Shapiro-Wilk normality test

data:  X[[4L]] 
W = 0.9328, p-value = 0.09032


$`9`

	Shapiro-Wilk normality test

data:  X[[5L]] 
W = 0.7837, p-value = 4.325e-05


> tapply(Wind,Month,shapiro.test)
$`5`

	Shapiro-Wilk normality test

data:  X[[1L]] 
W = 0.968, p-value = 0.4659


$`6`

	Shapiro-Wilk normality test

data:  X[[2L]] 
W = 0.9686, p-value = 0.501


$`7`

	Shapiro-Wilk normality test

data:  X[[3L]] 
W = 0.95, p-value = 0.1564


$`8`

	Shapiro-Wilk normality test

data:  X[[4L]] 
W = 0.9853, p-value = 0.937


$`9`

	Shapiro-Wilk normality test

data:  X[[5L]] 
W = 0.9785, p-value = 0.7852

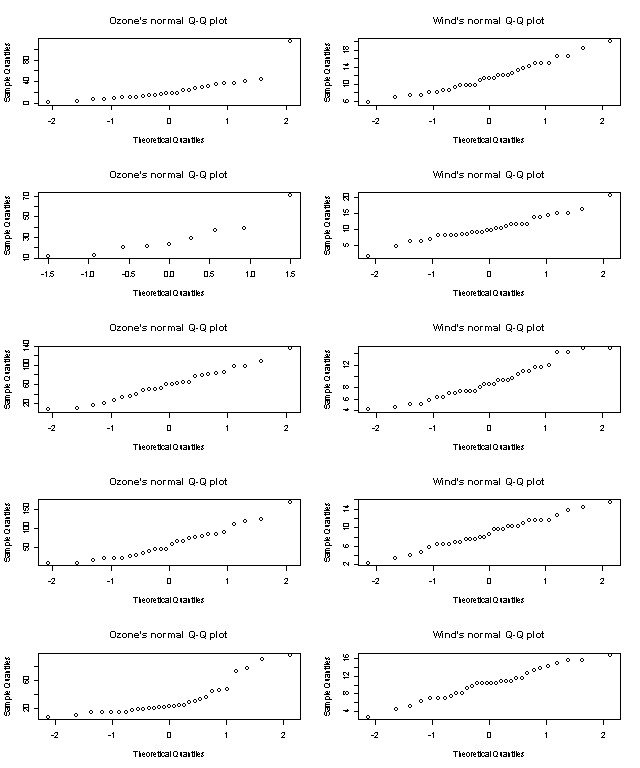
正規確率プロットは，左列のオゾン濃度も，右列の風速も，一番上が５月で一番下が９月である。まずオゾン濃度についてみると， Box C のグラフは，１日だけ極端にオゾン濃度の値が高い日があり，６月は欠損が多すぎるので何ともいえない。７月，８月はほぼ直線に乗っているように見えるが，９月は Box D ，直線性が低いようにみえる。風速については，５月，６月，８月，９月のグラフはほぼ直線に乗っているようにみえるが，７月は，オゾン濃度の９月と似ていて， Box D ，直線性が低いようにみえる。

Shapiro-Wilkの検定結果をみると，オゾン濃度の結果では，５月と９月のp-valueは8.294e-06と4.325e-05であり，どちらも有意水準である5％（つまり0.05）より小さいので，「データの分布は正規分布に従う」という帰無仮説が Box E （棄却される｜棄却されない）。つまり，５月と９月のオゾン濃度の分布は正規分布と統計学的に有意な差があるとはいえる。しかし，その他の月のp-valueは，すべて0.05より大きいので，帰無仮説が Box F （棄却される｜棄却されない）。風速については，すべての月の検定結果において，p-valueが0.05より大きかったので，帰無仮説が Box F （棄却される｜棄却されない）。つまり，５月と９月以外の月のオゾン濃度の分布とすべての月の風速の分布は，有意水準5％で正規分布と統計学的に有意な差があるとはいえないので，とりあえず正規分布に従っていると考えて差し支えない。

（注）なお，帰無仮説にデータが一致しすぎている場合もあって，そういう場合は捏造あるいは都合のいいデータだけを使った可能性を疑うべきである。有名な例はメンデルのエンドウマメであり，偶然のばらつきもあるはずなのに，それが極端に少なく，データが分離の法則に一致しすぎていたとフィッシャーが指摘している。他の例としては，第二水俣病発覚当時，昭和電工が出してきた上流域住民の毛髪中水銀濃度の分布が，対照地域の住民の毛髪中水銀濃度の分布と一致しすぎていたことが挙げられる。水銀汚染がないといいたいがために，差がなさ過ぎるデータを作ってしまったのであろうと言われている（出典：田栗正章・藤越康祝・柳井晴夫・C.R.ラオ『やさしい統計入門』講談社ブルーバックス）。

解答例

項目	入力欄
	qqnorm
	sharpiro.test
	５月
	４点（４日間）だけ高く外れた日があり，
	棄却される
	棄却されない

主なコメント・質問への回答など

検定結果について（文脈から推定できたが）

概ね次のように整理できますので，参考にしてください。Rの出力でp-valueとなっているのが有意確率です。有意水準は予め0.05か0.01か0.001に決めます。有意確率がどんなに小さくても差が大きいとは限りません。差がゼロではないことの確からしさが高まるだけですので，注意してください。

有意確率＜有意水準	有意確率≧有意水準
帰無仮説が棄却される	帰無仮説は棄却されない
データの分布と正規分布には統計学的な有意差がある	データの分布と正規分布には統計学的に有意な差はない
データは正規分布に従わない（データの分布は正規分布と異なるという意思決定ができる）	データが正規分布に従っていることは否定されない（データの分布が正規分布と異なるとは言えない）

英語が毎回小テストがあるので，遅刻の基準をあと２分甘くしてほしい（Bクラス）

分かりました。コンピュータが不調なこともあるので，10分まではOKとしましょう。

５月の結果が違います

出題ミスで申し訳ありません。Windの結果とOzoneの結果が混ざっていました。

qqnormってなんですか？

元々quantile-quantile plotの略でQQ plotという描画方法があります。２つの変数の値の関係をそのままの値で２次元平面にプロットすると散布図になりますが，quantile（分位数）に変換してプロットするとQQ plotになります（Rではqqplot()という関数を使います）。１つの変数について，生の値の分位数を縦軸に，正規分布に従うとした場合の分位数を横軸にとってプロットする関数がqqnorm()です。その図を正規確率プロット（Normal QQ plot）と呼びます。もしその変数が正規分布していれば，横軸と縦軸は正確に一致するので，データは直線に乗ります。この仮想的な直線を重ね書きしてくれる関数があって，qqline()です。

リンクと引用について