群馬大学 | 医学部 | サイトトップ | 医学情報処理演習
今回使った関数や文の主なものをまとめます (A selected summary of functions and statements used in the 6th practice is shown here.)
| 関数名(name) | 機能(effect) | 使い方(usage) |
|---|---|---|
| sqrt() | 平方根を計算する | sqrt(25)は5を返す。sqrt(c(1,9,16))はc(1,3,4)を返す。 |
| abs() | 絶対値を計算する | abs(5-7)は2を返す。abs(-2:2)はc(2,1,0,1,2)を返す。 |
| t.test(X, mu=a) | 一標本t検定 | ベクトルXの母平均値が数値aであるという帰無仮説のt検定を行う。mu=aを省略すると,mu=0の意味になる。 |
| rnorm(N,mu,sigma) | 正規乱数の発生 | 平均mu,標準偏差sigmaの正規分布に従う乱数をサイズNのベクトルとして返す |
| pt(t0,df) | t分布の分布関数 | 自由度dfのt分布のt0に対する分布関数の値を返す。この値を1から引けば,自由度dfのt分布に従う統計量tが偶然t0より大きい値をとる確率が得られる。 |
| var() | 不偏分散を求める | ベクトルの不偏分散を返す |
| pf(F0,dfx,dfy) | F分布の分布関数 | 第1自由度dfx,第2自由度dfyのF分布のF0に対する分布関数の値を返す。この値を1から引けば,第1自由度dfx,第2自由度dfyのF分布に従う統計量Fが偶然F0より大きい値をとる確率が得られる。 |
| var.test(X, Y) | 2群の分散に差が無いという帰無仮説のF検定 | XとYはそれぞれ数値ベクトル。長さは違っていてもいい。帰無仮説は分散の比が1ということ。 |
| var.test(X ~ B) | 2群の分散に差が無いという帰無仮説のF検定 | Xは数値ベクトル,Bは2水準の要因型のベクトル。長さが等しくなければならない。上の場合とはベクトルの与え方が異なるだけで同内容。つまり,var.test(X, Y)とvar.test(c(X, Y) ~ as.factor(c(rep("X",length(X)), rep("Y",length(Y)))))は同値なのである。同じデータフレーム内の変数ならば,data=オプションでデータフレーム名を指定すれば,データフレーム名$Xとせず,ただXと変数名を指定するだけでOK。(補足も参照) |
| t.test(X, Y) | 2群の平均値に差が無いという帰無仮説のt検定 | XとYはそれぞれ数値ベクトル。長さは違っていてもいい。等分散を仮定したt検定ではなく,不等分散でも使える,Welchの方法で自由度を調整したt検定を行う(仮にvar.test()で等分散性が棄却されなくても,Welchの方法で問題ないことがわかっている。var.test()はt.test()の前処理として行うのではなく,「分散に差が無い」という,t検定とは異なる帰無仮説を検定するために行う検定であると考えるべきである。どちらの検定の目的も2群のデータの分布の比較には違いない)。どうしても等分散性を仮定したt検定を実行したい場合は,var.equal=TRUEというオプションを指定すればよい。片側検定をしたい場合は,alternative="greater"(XがYより小さくなることはないと想定される場合)またはalternative="less"(その逆の場合)というオプションをつける。 |
| t.test(X ~ B) | 2群の平均値に差が無いという帰無仮説のt検定 | Xは数値ベクトル,Bは2水準の要因型のベクトル。長さが等しくなければならない。var.test()の場合と同じく,t.test()にも2種類のデータの与え方があり,こちらの与え方だと,同じデータフレーム内の変数ならば,data=オプションでデータフレーム名を指定し,データフレーム名$Xとせず,Xと変数名を指定するだけでOK。 |
| stripchart() | ストリップチャートを描く | stripchart(X ~ B, vert=TRUE, method="jitter")とすると,Bのカテゴリ毎に適当なまとまりを作って,すべてのXの値を縦軸にとり,適当に散らばらせてプロットしてくれる。同じ値が複数存在するときはplot()より見やすい。method="stack"とするとBのカテゴリ毎に左端が揃う。 |
| points() | 点を打つ | 既にグラフが描かれているウィンドウにX座標とY座標を指定して点を追記する。点の種類はpch=オプションで指定する。 |
| arrows() | 矢印を描く | 既にグラフが描かれているウィンドウに始点と終点のX座標とY座標を指定して矢印を追記する。code=3で両端に鏃が付き,angle=90で鏃が90度開く。 |
| rep(A,N) | 同一要素の繰り返し | 要素AをN回繰り返してつないだベクトルを返す。例えば,rep(1:2,5)は,c(1,2,1,2,1,2,1,2,1,2)と同値である。 |
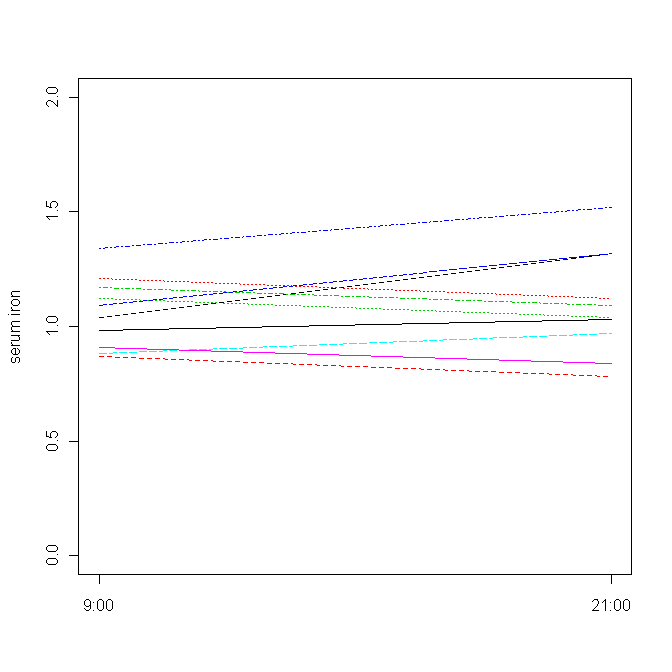
| t.test(X, Y, paired=TRUE) | 対応のある2群間の平均値の差の検定 | 対応のある2つの数値ベクトル(例えば食事療法による介入前後の空腹時血糖値とか)がX,Yという同じ長さのベクトルとして与えられている場合,t.test()関数にpaired=TRUEオプションを入れることで,対応のあるt検定(英語ではpaired t-test)が実行できる。数学的にはt.test(X-Y, mu=0)という一標本t検定と同値である。テキストの例題の場合,下のようにすると良い。matplot()は行を横軸(実は別に与えることもできるが……)として,行列の値を列ごとにプロットする(重ね描きする)関数である。type="p"で各データ点,type="l"でデータを結ぶ線,type="b"で両方をプロットする。xaxt="n"というオプションにより横軸の細かい数字を消すことができる。この例では横軸は時刻でありカテゴリ扱いするので,横軸の数字は,次の行のaxis(1,1:2,labels=c("9:00","21:00"))で後で描かせている。axis()の引数は,最初の1が横軸であることを意味し(2なら縦軸),次の1:2は1と2の位置に軸目盛があることを意味し(カテゴリ扱いする場合は自然数の位置にプロットされるため),次のlabels=c("9:00","21:00")は,軸目盛1と2の位置に表示させる文字列を指定している。BX <- c(0.98,0.87,1.12,1.34,0.88,0.91,1.04,1.21,1.17,1.09)
AX <- c(1.03,0.78,1.04,1.52,0.97,0.84,1.32,1.12,1.09,1.32)
t.test(BX, AX, paired=TRUE)
matplot(rbind(BX,AX),type="l",xaxt="n",xlab="",ylim=c(0,2),ylab="serum iron")
axis(1,1:2,labels=c("9:00","21:00")) |
| 補足 | 2群のデータの相互形式変換(1) | set.seed(1)の後,X1 <- rnorm(100,120,10)とX2 <- rnorm(100,110,10)により,架空の独立2群についての数値ベクトルX1とX2が得られる。これをデータフレームxに変換するには,Z <- c(X1,X2)
B <- as.factor(c(rep("X1",100),rep("X2",100)))
x <- data.frame(Z,B)とする。分散に差が無いという帰無仮説の検定や平均値に差が無いという帰無仮説の検定ならばどちらの形のデータでもいいが(例えばvar.test(X1,X2)とvar.test(Z~B, data=x)は全く同じ結果になる),2群を層として並べて層別箱ひげ図や層別のstripchartを描かせるにはデータフレームとしておく方がいいし,表計算ソフトで入力したデータをタブ区切りテキストとしてread.delim()関数で読み込む場合,読み込まれたデータはデータフレームになるので,データフレームの形でデータを保持するのがより一般的である。 |
| 2群のデータの相互形式変換(2) | 実はこの操作をするための関数も存在する。名前付きの2つの要素をもつリストは,stack()関数によってデータフレームに変換できる。x <- stack(list(X1=X1,X2=X2)) 逆に,1列目の変数が数値型,2列目の変数が要因型であるデータフレームは,unstack()関数によって,要因ごとのリストに変換できる。 X1 <- unstack(x)[[1]] X2 <- unstack(x)[[2]] |