| 被検者 | 恐怖 | 幸福 | 落胆 | 沈着 |
|---|---|---|---|---|
| 1 | 23.1 | 22.7 | 22.5 | 22.6 |
| 2 | 57.6 | 53.2 | 53.7 | 53.1 |
| 3 | 10.5 | 9.7 | 10.8 | 8.3 |
| 4 | 23.6 | 19.6 | 21.1 | 21.6 |
| 5 | 11.9 | 13.8 | 13.7 | 13.3 |
| 6 | 54.6 | 47.1 | 39.2 | 37.0 |
| 7 | 21.0 | 13.6 | 13.7 | 14.8 |
| 8 | 20.3 | 23.6 | 16.3 | 14.8 |
x <- matrix(c(
1,23.1,22.7,22.5,22.6,
2,57.6,53.2,53.7,53.1,
3,10.5, 9.7,10.8, 8.3,
4,23.6,19.6,21.1,21.6,
5,11.9,13.8,13.7,13.3,
6,54.6,47.1,39.2,37.0,
7,21.0,13.6,13.7,14.8,
8,20.3,23.6,16.3,14.8),8,5,byrow=TRUE) # データを行列として入力
colnames(x) <- c("subj","fear","happiness","despair","calmness") # 刺激の種類を定義
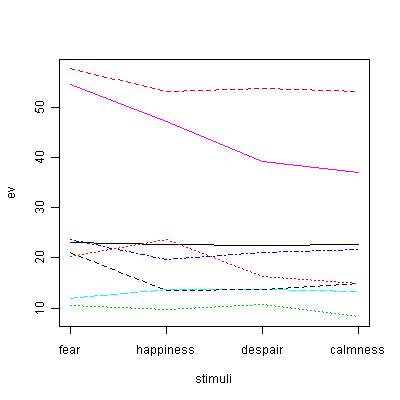
matplot(t(x[,-1]), type="l", ylab="ev", xlab="stimuli", xaxt="n") # 4種類の刺激に対する個人ごとの電位をプロット
axis(1, 1:4, colnames(x[,-1])) # グラフの横軸に刺激の種類を表示
mx <- colMeans(x[,-1]) # 各刺激についての電位の平均値。apply(x[,-1],2,mean)と同値。
sx <- apply(x[,-1],2,sd) # 各刺激に対する電位の標準偏差
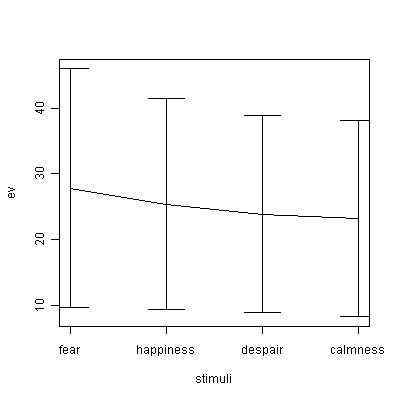
plot(1:4,mx,type="l",ylim=c(min(mx-sx),max(mx+sx)),ylab="ev",xlab="stimuli",xaxt="n") # 4種類の刺激に対する平均電位をプロット
arrows(1:4,mx-sx,1:4,mx+sx,code=3,angle=90) # 標準偏差のひげをプロット
axis(1, 1:4, colnames(x[,-1])) # グラフの横軸に刺激の種類を表示
dat <- data.frame(
subj=rep(x[,1],4),
emst=gl(4,8,labels=c("fear","happiness","despair","calmness")),
ev=c(x[,2],x[,3],x[,4],x[,5])) # 縦長データフレームの定義
friedman.test(ev ~ emst | subj, data=dat) # フリードマンの検定。このデータでは有意水準5%で有意ではない。
library(car) # Anova()関数を使うためcarライブラリをロード
stimuli <- factor(colnames(x[,-1]), ordered=FALSE) # 刺激種類を要因型変数として定義
rep.anova <- Anova(lm(x[,-1]~1), idata=data.frame(stimuli), idesign= ~stimuli, type="III") # 反復測定分散分析実行
summary(rep.anova, multivariate=FALSE) # 結果の表示。G-G補正やH-F補正をしたp値は0.05より大きい。
# avova(lm(ev ~ emst+subj, data=dat)) として二元配置分散分析するより切れ味がよい。
# oneway.test(ev ~ emst, data=dat) として個人差を無視してしまうと,刺激による差はマスクされる。
| 被験者 | 1時間前 | 投与直前 | 1h | 2h | 3h | 4h | 5h | 6h | 7h | 8h |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 112 | 119 | 113 | 105 | 114 | 110 | 115 | 114 | 110 | 111 |
| 2 | 116 | 110 | 115 | 110 | 112 | 107 | 116 | 115 | 120 | 118 |
| 3 | 122 | 123 | 126 | 114 | 111 | 113 | 119 | 123 | 119 | 124 |
| 4 | 124 | 130 | 127 | 110 | 100 | 127 | 130 | 134 | 120 | 124 |
| 5 | 126 | 121 | 115 | 122 | 124 | 117 | 124 | 132 | 128 | 120 |
| 6 | 129 | 135 | 125 | 122 | 115 | 110 | 114 | 124 | 133 | 131 |
z <- matrix(c(
1,112,119,113,105,114,110,115,114,110,111,
2,116,110,115,110,112,107,116,115,120,118,
3,122,123,126,114,111,113,119,123,119,124,
4,124,130,127,110,100,127,130,134,120,124,
5,126,121,115,122,124,117,124,132,128,120,
6,129,135,125,122,115,110,114,124,133,131),6,11,byrow=TRUE) # データを行列として入力
colnames(z) <- c("subj","T.1","T0","T1","T2","T3","T4","T5","T6","T7","T8") # 変数名定義
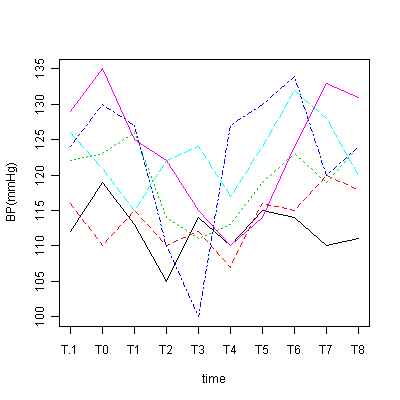
matplot(t(z[,-1]), type="l",ylab="BP(mmHg)",xlab="time",xaxt="n") # 個人ごとの経時変化パタンをプロット
axis(1,1:10,labels=colnames(z[,-1])) # 横軸ラベル表示
mx <- colMeans(z[,-1]) # 各時点での血圧平均値。apply(z[,-1],2,mean)と同値。
sx <- apply(z[,-1],2,sd) # 各時点での血圧の標準偏差
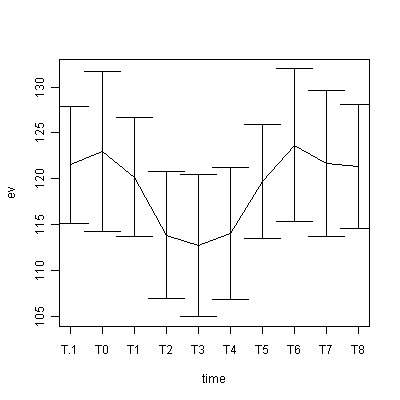
plot(1:10,mx,type="l",ylim=c(min(mx-sx),max(mx+sx)),ylab="ev",xlab="time",xaxt="n") # 各時点での平均血圧をプロット
arrows(1:10,mx-sx,1:10,mx+sx,code=3,angle=90) # 標準偏差のひげをプロット
axis(1,1:10,labels=colnames(z[,-1])) # 横軸ラベル表示
dat2 <- data.frame(
subj=factor(rep(z[,1],10)),
tvars=gl(10,6,labels=colnames(z[,-1])),
BP=as.vector(z[,-1])) # フリードマンの検定や分散分析のための縦長データフレームの定義
friedman.test(BP ~ tvars | subj, data=dat2) # フリードマンの検定。個人差を考慮すると時点の有意な効果がある。
# 本来は下記だが,時点数より人数が少ないと行列が計算できずエラーになる
# library(car) # Anova()関数を使うためcarライブラリをロード
# times <- factor(colnames(z[,-1])) # 時点変数を要因型変数として定義
# rep.anova.2 <- Anova(lm(z[,-1]~1), idata=data.frame(times), idesign=~times, type="II") # 分析実行(→エラー)
# summary(rep.anova.2, multivariate=FALSE) # 分散分析の結果を表示
# そこで,下記を実行
res1 <- aov(BP ~ subj + tvars, data=dat2) # 通常の二元配置分散分析の実行結果を得る
summary(res1) # 結果を表示
mlmfit1 <- lm(z[,-1]~1) # anova.mlmによる反復測定分散分析
mlmfit0 <- lm(z[,-1]~0) # まず,このように2つのオブジェクトを計算する
anova.mlm(mlmfit1, mlmfit0, X=~1, test="Spherical") # これでSASのPROC GLMのREPEATEDと同じ結果が得られる