(WHnd <- ![]() ) # make a frequency table of Writing Hand and print it.
) # make a frequency table of Writing Hand and print it.
群馬大学 | 医学部 | サイトトップ | 医学情報処理演習
第9回に出てきた関数と文の主なものはこちらを参照されたい。
MASSライブラリに含まれているsurveyというデータは,アデレード大学で統計学Iを選択した学生237人にいくつかの質問をした結果を含んでいる。このうち,W.Hndという変数は,利き手を示す要因型変数である。
(1) この学生たちのうち,左利きの割合を求めよ。ただし欠損は両利きとみなし,分母に含めること。
一方,利き手にはあまり国や民族による差はないといわれており,Wikipediaでは成人の8〜15%が左利きというデータが紹介されている。また,Wiiという任天堂のゲーム機を用い,全世界のユーザを対象とした「投票チャンネル」機能で2007年9月に集計された結果では,14.2%が左利きであった。
(2) 仮に,この14.2%という値が母集団における左利きの割合だとして,アデレード大学の統計学Iを選択した学生の左利きの割合はそれと差があるかどうか,有意水準5%で検定せよ。
以上の(1)(2)について解析手順を示すので,学籍番号・氏名とともに,下のフォームを穴埋めして送信せよ。
まず,データを読み込むためにMASSライブラリをメモリにロードする。
library(MASS)
これでsurveyというデータフレームが使えるようになっているはずなので,その中に含まれているW.Hndという変数について度数分布を求め,結果をWHndというオブジェクトに付値し,それを画面に表示してみる(文全体を括弧でくくると,自動的にprint関数にオブジェクトが渡されるので画面表示される)。
(WHnd <-
) # make a frequency table of Writing Hand and print it.
以下のように表示されるので,237人中,左利きが18人,右利きが218人,欠損が1人とわかる。ここでは欠損の人を両利きと見なし,以下左利きの割合を計算する場合の分母に含める。
Left Right NA's 18 218 1
円グラフを描いてから,この学生のうちの左利きの割合(よりも偏る場合)が,母比率が0.142であるときに偶然起こる確率を二項検定によって求めるコードは下記2行。
pie(WHnd) # draw pie chart
# execute exact binomial test
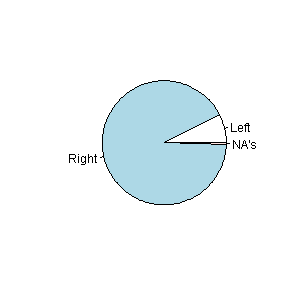
円グラフは上のようになり,4分の3以上が右利きであることは一目瞭然である。二項検定の結果は下記の通り。
Exact binomial test
data: WHnd["Left"] and sum(WHnd)
number of successes = 18, number of trials = 237, p-value = 0.00273
alternative hypothesis: true probability of success is not equal to 0.142
95 percent confidence interval:
0.04563171 0.11737794
sample estimates:
probability of success
0.07594937この結果から,(1)左利き学生の割合は![]() %(95%信頼区間は4.5〜11.8%),(2)有意確率は0.00273と5%より遥かに小さいので,アデレード大学の統計学I選択学生の左利き割合が母比率と差がないという帰無仮説は
%(95%信頼区間は4.5〜11.8%),(2)有意確率は0.00273と5%より遥かに小さいので,アデレード大学の統計学I選択学生の左利き割合が母比率と差がないという帰無仮説は![]()
| 項目 | 解答例 |
|---|---|
| summary(survey$W.Hnd) | |
| binom.test(WHnd["Left"],sum(WHnd),0.142) または binom.test(18,237,0.142) | |
| 7.6 | |
| 棄却される。 |
(注)["Left"]は[''Left'']ではありませんし[”Left”]でもありません。文字列は半角の二重引用符で括ります。