群馬大学 | 医学部 | サイトトップ | 医学情報処理演習
医学情報処理演習：2011年度第6回課題
第6回に出てきた関数と文の主なものはこちらを参照されたい。
課題
http://phi.med.gunma-u.ac.jp/medstat/sample02.txtは，ソロモン諸島の首都のとある学校で実施した健診結果のタブ区切りテキスト形式データである。このデータを読み込んで，男女(SEX)間で収縮期血圧mmHg(SBP)の平均値に差が無いという帰無仮説を，有意水準5％で検定するためのコードと出力結果とその解釈を下に示す。学籍番号・氏名とともに，下のフォームと解釈文を穴埋め［Box AとBには適切な関数名を入力し，CとDとFにその次の（ ）内から適切な方を選択して数字で入力，Eに適切な数値を入力］して送信せよ。
(Please fill the boxes A and B by adequate function names, and fill the boxes C, D and F by the number 1 or 2, selecting from the following 2 candidates with parenthesis, and fill the box E by the adequate figures. Here we assume the significance level of statistical test as 0.05.)
まず，下記のコードを実行する。
x <- read.delim("http://phi.med.gunma-u.ac.jp/medstat/sample02.txt") # データをxに読み込む
Mx <- tapply(x$SBP,x$SEX,
) # 男女別にSBPの平均値を求める (Calculate means of SBP by SEX)
Sx <- tapply(x$SBP,x$SEX,
) # 男女別にSBPの不偏標準偏差を求める (Calculate standard deviations of SBP by SEX)
stripchart(SBP ~ SEX, data=x, method="jitter", vert=TRUE) # 男女層別にSBPのストリップチャートを描く
points(1:2+0.1,Mx,pch=18) # データ各点が描かれた右に男女別に平均値を追加プロット
arrows(1:2+0.1,Mx-Sx,1:2+0.1,Mx+Sx,angle=90,code=3) # 平均値の点の上下に不偏標準偏差の長さのエラーバーを表示
var.test(SBP ~ SEX, data=x) # 男女間でSBPの分散に差が無いという帰無仮説をF検定
t.test(SBP ~ SEX, data=x) # 男女間でSBPの平均値に差が無いという帰無仮説をWelchの方法でt検定
結果として，グラフが描画された後でSBPの分散に性差が無いという帰無仮説の検定結果と，平均値に差が無いという帰無仮説の検定結果が表示される。
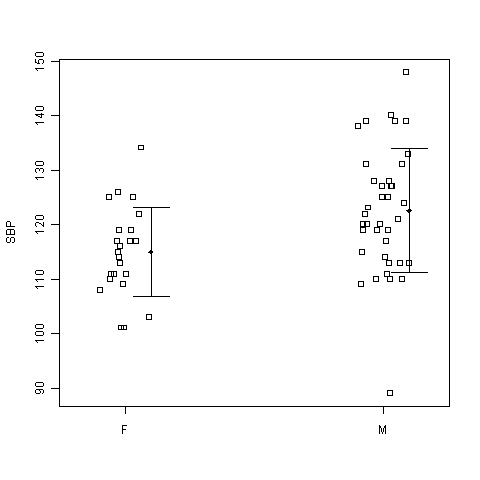
グラフを見ると，
（1. 女性の方が男性よりも｜2. 男性の方が女性よりも），全体としてSBPの値が小さいところに分布しているが，ばらつきは
（1. 女性の方が男性よりも大きく｜2. 男性の方が女性よりも大きく｜3. 男女とも同程度に）見える。
(The SBP data of (1. Females distributes in lower ranges than those of Males | 2. Males distributes in lower ranges than those of Females). However, the variances of SBP looks (1. larger in Females than in Males | 2. larger in Males than in Females | 3. almost similar in Females and in Males).)
SBPの分散に性差が無いという帰無仮説のF検定の結果，有意確率(p-value)は
なので，この帰無仮説は棄却されない。一方，SBPの平均値に性差が無いという帰無仮説についてのWelchのt検定を行った結果では，有意確率が0.003891と有意水準である0.05より小さかったので，帰無仮説は棄却
（1. される｜2. されない）。SBPの平均値には，有意水準5％で，統計学的に有意な性差があったといえる。
(As the result of F-test to test the null-hypothesis that the variances of SBP is same between males and females, the p-value was , which means that the null-hypothesis couldn't be rejected. The Welch's t-test for the null-hypothesis that means of SBP are not different by sex resulted p-value less than 0.05. By this result, we (1. can | 2. cannot) reject the null-hypothesis. Thus the means of SBP are significantly different between males and females at 5% level.)
解答フォーム
リンクと引用について