MASSライブラリに含まれているデータフレームAids2は,1991年7月までのオーストラリアにおいて,AIDSと診断された患者2843人のデータである。含まれている変数は,stateが元々の居住州(NSWかQLDかVICかその他)を示し,sexは性別(Fが女性でMが男性),diagが診断日,deathが死亡または観察終了日,statusは死亡か生存か(Dが死亡,Aが生存),T.categは感染経路,ageは診断時の年齢である。
このデータは本来なら生存時間解析をするべき,前向きコホート研究のデータであるが,2×2のクロス表で男女間で死亡を比較することもできる。何を指標としたか明記した上で男女間で死亡を比較し解釈せよ。なお,検定を用いる場合は,有意水準5%とすること。
- 難しかった(多数)
- 新しいタイプの課題だったので,難しかったかもしれません。この課題に解答するためのポイントは2点あります。
- (1)疾病量の指標としては何を使うべきか (2)比較は差と比のどちらで行うべきか
- (1)まず,このタイプの研究では,曝露が何でアウトカムが何かということをはっきりさせなくてはいけません。この研究で比較したいのは男女間での死亡なので,曝露は性別,アウトカムは死亡です。データはどのように取られているかというと,診断日から死亡あるいは観察終了までの日数があることから,コホート研究であることがわかります。性別は診断日の時点で既知なので,男女別に何人ずつを観察していたらそのうち何人ずつが死亡するかを計算できますので,累積死亡率,つまりリスクを計算することができます。したがって,疾病量の指標としてはリスクを使うべきです(もちろん,日数データが含まれていますので,観察人年を分母として死亡率を計算することも可能ですが,そこまでやるなら打ち切りレコードを考慮して分析できる生存時間解析をすべきです)。
- (2)比較は差でも比でもそれぞれの意味がありますが,このデータの場合は,おそらく男女間の相対的な比較を目的としているので(1991年までの絶対的な差をみても何の役に立つのか不明なので),比でみるのが適切でしょう。
- ただし,コホート研究で死亡オッズを計算することが無意味かというと,まったく無意味であるとも言い切れませんので,男女間で死亡オッズの比を出してオッズ比を検討することも間違いとは言い切れません。しかしコホート研究ですので,リスク比やリスク差の方がより適切です。
- 男女のサンプルサイズが違いすぎるが不適切ではないか
- サンプルサイズが違うと検出力が落ちるのが最大の問題点です。もし最初から男女の比較を目的に実験計画をしたならサイズを揃えるか,せいぜい数倍程度の違いにするのが普通ですが,このデータは1991年時点のオーストラリアのAIDS患者の全数なので仕方ありません。そう考えると,このデータをオーストラリアのAIDS患者全体を母集団とするサンプルと考えていいのかどうかも問題があるので,そもそも通常の統計処理をすること自体にも問題があるのかもしれません。
- fisher.test()関数とoddsratio()関数でp値やオッズ比が若干異なるが誤差範囲といえるのか
- 誤差範囲というよりも,求め方の違いです。oddsratio()関数のオッズ比は定義通りなので説明不要で使えますが,fisher.test()関数のオッズ比は超幾何分布を仮定した最尤推定値ですので,そのように書く必要があります。
- oddsratio()の結果に出る[Disease/Nondisease]と[Exposed/Nonexposed]の表示は変更できないか?
- 現在のところできません。確かに,このデータに使う場合は[Exposed/Nonexposed]ではなく[Females/Males],[Disease/Nondisease]ではなく[Dead/Alive]としたいところですね。fmsbライブラリをバージョンアップする時に考慮します。
- 生存時間解析をやってみたが合っているか
- 意欲的な取り組み,素晴らしいと思います。やってくれたRのコードの生存時間解析に該当する部分は下記です。やり方は基本的に合っていると思いますが,コックス回帰の共変量としてstateやageを使うなら,いきなりコックス回帰に入れるのではなく,その前に別のやり方でも検討しておくべきかもしれません(例えば,statusがAかDかで年齢を比較しておくとか,statusとstateのクロス集計をしておくとか:注:この部分,当初コード中のstateをstatusと勘違いして妙な解説をしていましたが,1月29日に書き直しました。申し訳ありません)。詳しくは,このサイト内にある,生存時間解析入門が参考になると思います。
#libraryの読み込み
library(MASS)
library(survival)
library(date)
#データ読み込み
data(Aids2)
#生存時間解析
str(Aids2)
summary(Aids2)
Aids2$event <- ifelse(status == "D", 1, 0) #statusを0,1に変換
#event発生までの日数を算出(diagを開始日とした)
Aids2$event.days <- as.numeric(as.Date(death, origin = "1960-01-01") - as.Date(diag, origin = "1960-01-01"))
(res <- survfit(Surv(event.days, event)~sex, data = Aids2))
plot(res, lty = c(1, 2))
summary(res)
#ログランク検定
survdiff(Surv(event.days, event)~sex, data = Aids2)
#Cox比例ハザードモデル
coxph(Surv(event.days, event)~sex + state + age)
- 丁寧にやっていてよいと思います。中澤なら少し手抜きをして(例えば比較演算子の結果のTRUE/FALSEは数値としては1/0であることなどを利用しますし,「日付データの扱い方はまだ説明していない」というのはSurv()が必要な意味づけの話で,ここで必要な日数計算は既にユリウス日になっているのでas.Date()を使ってDateクラスオブジェクトに変換する必要はありませんし,as.Date()関数はbaseパッケージに入っているので追加パッケージは不要です)次のように書くと思います。また,このデータでは打ち切り(終了時に生存している)レコードが多すぎて,グラフに出してしまうと男女間の比較がしにくいので,打ち切りレコードのマークを表示しない設定(mark.time=FALSE)にしました。
library(MASS); library(survival)
(res <- survfit(Surv(death-diag, status=="D") ~ sex, data=Aids2)) # カプラン=マイヤ法の計算と結果表示
layout(t(1:2)) # グラフィック画面を左右2分割
plot(res, main="カプラン=マイヤ法による生存曲線", lty=1:2, mark.time=FALSE) # 生存曲線の男女別プロット(女性が実線,男性が破線)
legend("topright", lty=1:2, legend=names(table(Aids2$sex))) # 凡例表示
survdiff(Surv(death-diag, status=="D") ~ sex, data=Aids2) # ログランク検定。有意でないので,たぶんここで止めてもいい。
plot(res, main="二重対数プロット", fun="cloglog", lty=1:2, mark.time=FALSE) # コックス回帰していいかどうか二重対数プロット
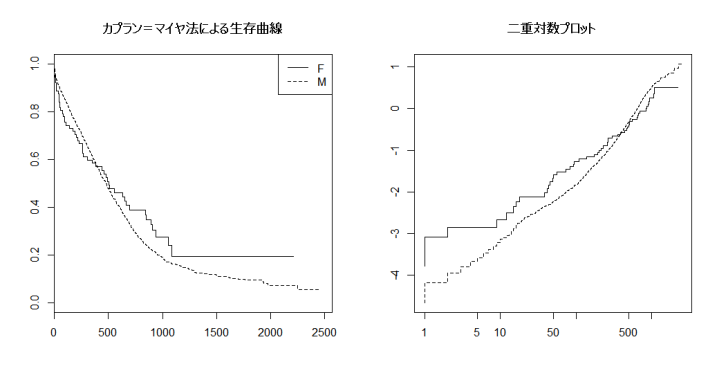
- 男女別の生存日数の中央値としてのカプラン=マイヤ推定量は,男性479日(95%信頼区間が[449, 500]),女性506日(同じく[303, 850])で違いがなく,ログランク検定の結果もp値が0.363なので,統計学的に生存日数に有意な違いがあるとはいえません。
- なお,診断後非常に短期間で亡くなるのは男性より女性の方が多いのですが,500日あたりで逆転し,それ以降は男性の方が早く亡くなっていることがわかります。おそらく女性のエイズ患者は不均質で,診断後非常に短期間で亡くなっているのは重症化するまで医療機関を受診せずにいた社会的階層が低い人たち(Commercial Sex Workerなども含めて)で,そうでない女性は男性よりも平均的には長生きなのではないかといった推論ができます(もちろん,それが本当であるという保証はないので,次の段階ではそれを検証するようなデザインで別の研究をすることになるでしょう)。
- 二重対数プロットで2本の線が平行でないので比例ハザード性の仮定は不適切と考えられ,通常はここで分析は終わりです。それでも敢えて強引に続けると,下記のようになります。
stripchart(age ~ status, data=Aids2, vert=TRUE, method="jitter") # 生死別に年齢をプロット
reg <- coxph(Surv(death-diag, status=="D") ~ sex, data=Aids2) # 年齢は影響なさそうなので性別だけを説明変数にしてコックス回帰
summary(reg)
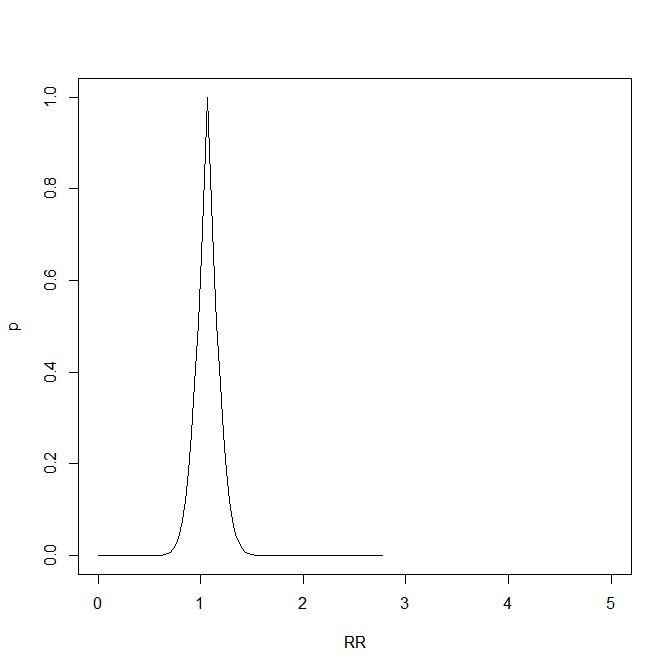
- コックス回帰の結果,sexMのexp(coef)の値が1.135なので,男性の女性に対する死亡ハザード比が1.135(95%信頼区間が[0.86, 1.50])で,尤度比検定でもウォルドの検定でもログランク検定と同じくp値は約0.36ですので,有意水準5%で男女間に死亡の有意な差は認められなかったということになります。