群馬大学 | 医学部 | サイトトップ | Software Tips | RについてのTips
最終更新: 2009年 6月 18日 (木曜日) 20時41分 :作成
このページは,群馬大学公衆衛生学教室において毎週行っている疫学・社会医学勉強会の月曜日枠「R実践活用」で,2008年11月17日から2009年6月15日まで,約半年をかけて読んだ,「観察疫学研究における生存時間解析」というチュートリアル論文(Bull K, Spiegelhalter DJ: Tutorial in biostatistics: Survival analysis in observational studies. Statistics in Medicine, 16: 1041-1074, 1997)の内容を紹介し,Rを使ってそれを実行する方法と,出力結果の解釈について解説する目的で設置する。Rを使った生存時間解析の一助になれば幸いである。
多施設データベースが確立したものになってくるにつれて,リスク因子と時間に臨床的な結果を関連付ける報告が多数出現しつつある。これらの研究は,多様な目的をもっている。ある一群の患者が経験することの記述であるかもしれないし,リスク因子の同定であるかもしれないし,意思決定のための個人についての予測であるかもしれない。そして,増加しつつあるのが,施設間比較,あるいは施術者間比較のための標準化(リスク層別化)という目的である。研究者はまた,代替的な介入あるいは臨床戦略の効果についても結論を引き出したいと思うかもしれない(データベースの分析から治療の利益についての判断を下すことの危険性は,既によく議論されてきてはいるけれども)。
| Patient | agepres | agelast | ageop1 | dead | sex | paanat | adfol | follow-up | opfpres | unopage | unopfpre | preopded | hadop | ded-lyrpp | age-presx |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1274 | -1 | 0 | 0 | 0 | 1 | 1273 | -1 | 1274 | 1273 | 0 | 0 | 0 | 0 |
| 2 | 2 | 123 | 40 | 1 | 0 | 1 | 1 | 121 | 38 | 40 | 38 | 0 | 1 | 1 | 0 |
| 3 | 2 | 119 | -1 | 1 | 1 | 0 | 1 | 117 | -1 | 119 | 117 | 1 | 0 | 1 | 0 |
| 4 | 3 | 120 | -1 | 0 | 1 | 0 | 0 | 117 | -1 | 120 | 117 | 0 | 0 | 2 | 0 |
| 5 | 6 | 10 | -1 | 1 | 0 | 0 | 1 | 4 | -1 | 10 | 4 | 1 | 0 | 1 | 0 |
| 6 | 6 | 5415 | 194 | 0 | 0 | 1 | 1 | 5409 | 188 | 194 | 188 | 0 | 1 | 0 | 0 |
| 7 | 7 | 3261 | 1041 | 0 | 1 | 0 | 1 | 3254 | 1034 | 1041 | 1034 | 0 | 1 | 0 | 0 |
| 8 | 8 | 1819 | -1 | 0 | 1 | 0 | 1 | 1811 | -1 | 1819 | 1811 | 0 | 0 | 0 | 0 |
| 9 | 11 | 696 | -1 | 0 | 0 | 0 | 1 | 685 | -1 | 696 | 685 | 0 | 0 | 0 | 0 |
| 10 | 13 | 6415 | 29 | 0 | 1 | 1 | 1 | 6402 | 16 | 29 | 16 | 0 | 1 | 0 | 0 |
| 11 | 29 | 3127 | 144 | 1 | 0 | 0 | 1 | 3098 | 115 | 144 | 115 | 0 | 1 | 0 | 0 |
| 12 | 30 | 423 | 47 | 1 | 0 | 0 | 1 | 393 | 17 | 47 | 17 | 0 | 1 | 0 | 0 |
| 13 | 35 | 5794 | -1 | 0 | 1 | 0 | 1 | 5759 | -1 | 5794 | 5759 | 0 | 0 | 0 | 0 |
| 14 | 45 | 292 | 62 | 1 | 1 | 1 | 1 | 247 | 17 | 62 | 17 | 0 | 1 | 1 | 0 |
| 15 | 54 | 68 | -1 | 1 | 1 | 0 | 1 | 14 | -1 | 68 | 14 | 1 | 0 | 1 | 0 |
| 16 | 58 | 1849 | -1 | 1 | 0 | 0 | 1 | 1791 | -1 | 1849 | 1791 | 1 | 0 | 0 | 0 |
| 17 | 68 | 343 | -1 | 1 | 1 | 0 | 1 | 275 | -1 | 343 | 275 | 1 | 0 | 1 | 0 |
| 18 | 109 | 3276 | 1294 | 0 | 0 | 0 | 1 | 3167 | 1185 | 1294 | 1185 | 0 | 1 | 0 | 0 |
| 19 | 119 | 207 | 207 | 1 | 0 | 1 | 1 | 88 | 88 | 207 | 88 | 0 | 1 | 1 | 0 |
| 20 | 121 | 1430 | 123 | 0 | 1 | 0 | 1 | 1309 | 2 | 123 | 2 | 0 | 1 | 0 | 0 |
| 21 | 231 | 308 | 237 | 1 | 0 | 1 | 1 | 77 | 6 | 237 | 6 | 0 | 1 | 1 | 0 |
| 22 | 258 | 347 | -1 | 0 | 0 | 0 | 0 | 89 | -1 | 347 | 89 | 0 | 0 | 2 | 0 |
| 23 | 349 | 3355 | 383 | 0 | 0 | 0 | 1 | 3006 | 34 | 383 | 34 | 0 | 1 | 0 | 0 |
| 24 | 369 | 3351 | 2826 | 1 | 0 | 1 | 1 | 2982 | 2457 | 2826 | 2457 | 0 | 1 | 0 | 1 |
| 25 | 437 | 547 | 441 | 0 | 0 | 0 | 0 | 110 | 4 | 441 | 4 | 0 | 1 | 2 | 1 |
| 26 | 771 | 3834 | 868 | 0 | 0 | 0 | 1 | 3063 | 97 | 868 | 97 | 0 | 1 | 0 | 1 |
| 27 | 1285 | 7209 | -1 | 0 | 1 | 0 | 1 | 5924 | -1 | 7209 | 5924 | 0 | 0 | 0 | 1 |
| 28 | 2455 | 3555 | 3532 | 1 | 1 | 1 | 1 | 1100 | 1077 | 3532 | 1077 | 0 | 1 | 0 | 1 |
| 29 | 5161 | 5354 | 5353 | 1 | 1 | 1 | 1 | 193 | 192 | 5353 | 192 | 0 | 1 | 1 | 1 |
| 30 | 5497 | 5639 | 5633 | 1 | 0 | 1 | 1 | 142 | 136 | 5633 | 136 | 0 | 1 | 1 | 1 |
表のままだと欠損値が-1になっているので,Rで扱うにはNAに置き換えねばならない。学生がExcelで入力してくれたファイルをタブ区切りテキスト形式で保存し,-1をNAに置換したファイルを,surv.txtとして置いておく。
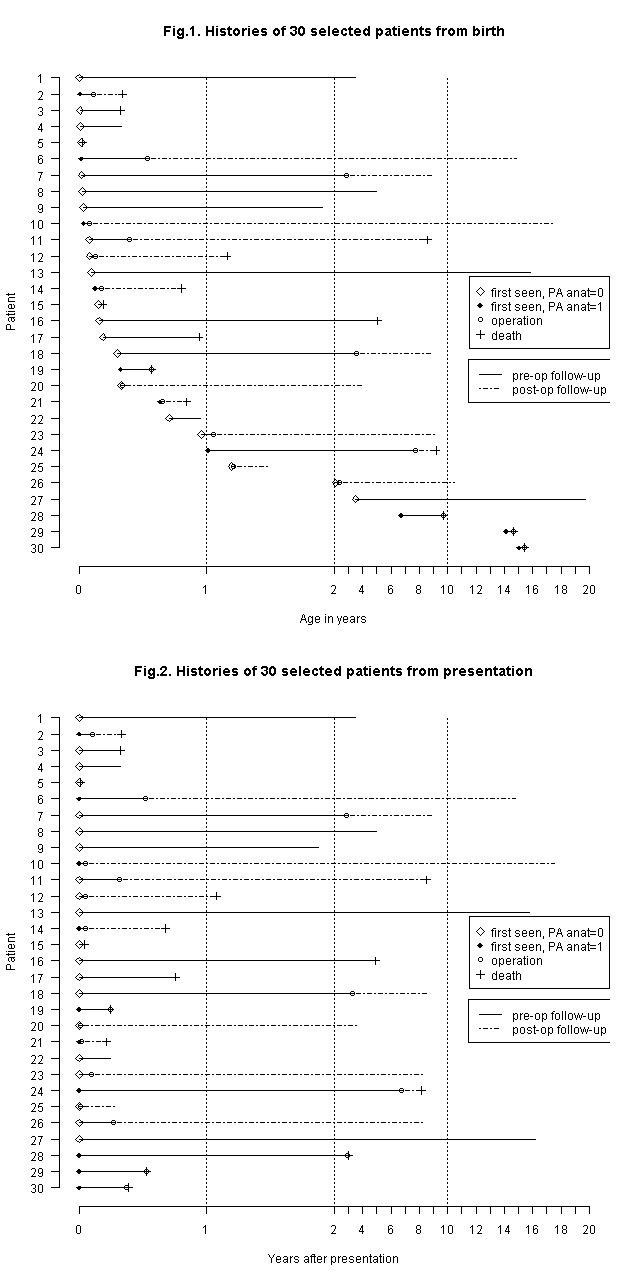
上図を描くためのコードは,plotx.Rである。画像はファイル出力されてしまうので注意されたい。
カプラン=マイヤ法による生存曲線の推定法を説明している。打ち切り例は,リスク集合から順次除かれていくことにより,適切に処理される。
表3にカプラン=マイヤ法の計算が示されている。表3と図3に掲載されている情報がわかるプログラムコードをweibull.Rに示す。実行すると下図がpng形式のファイルとして出力されてしまうので注意されたい。
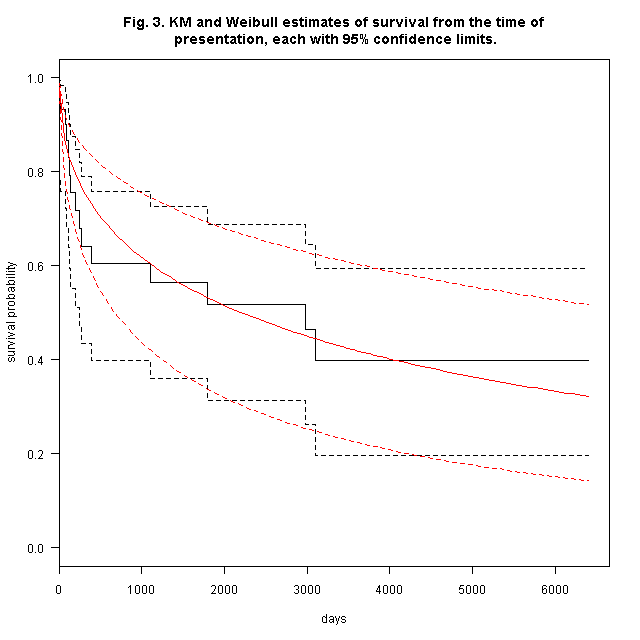
ちなみに,後で詳述するが,ワイブル関数をあてはめた結果は以下の通り。
Call:
survreg(formula = eventtime ~ 1, dist = "weibull")
Value Std. Error z p
(Intercept) 8.494 0.600 14.15 1.81e-45
Log(scale) 0.775 0.221 3.51 4.52e-04
Scale= 2.17
Weibull distribution
Loglik(model)= -128.6 Loglik(intercept only)= -128.6
Number of Newton-Raphson Iterations: 5
n= 30カプラン=マイヤ法を数学的に表現すると,時点tkにおいてk番目の死が起こり,その時点でのリスク集合のサイズがrkだったとし,その時点で起こった死亡数がfkだったとすれば,時点tkまでの生存確率の推定値pkは,
pk=(1-f1/r1)(1-f2/r2)...(1-fk/rk)
となる。
左側切捨て[left-truncation]あるいは遅れて参加すること[late entry]の問題。例えば子供時代の生存については,成人になってから研究に参加した患者についての情報では何もいえないが,通常,右側打ち切りと同じく,左側切捨ても情報量が無い[non-informative late entry]と仮定する。即ち,同じ年齢で既に研究に参加していた人と本質的に同等であったと見なす。
表4(a)に示すように,誕生からの生存年数は普通にカプラン=マイヤ法で計算できるが,リスク集合の中に,そのイベント発生年齢では研究にまだ参加していなかった人を含めてしまうのは不合理である。そこで,そういう人をリスク集合から除いてカプラン=マイヤ法をやり直すと,表4(b)のように計算でき,下図のようにグラフが描ける。これを実行するRコードは,table4fig4.Rである(これも実行するとカレントディレクトリにpngファイルができてしまうので注意)。この計算はあまりなされないため,survfit()関数に元々は組み込まれておらず,いちいち計算させる必要があって,多少プログラムが複雑になっている。
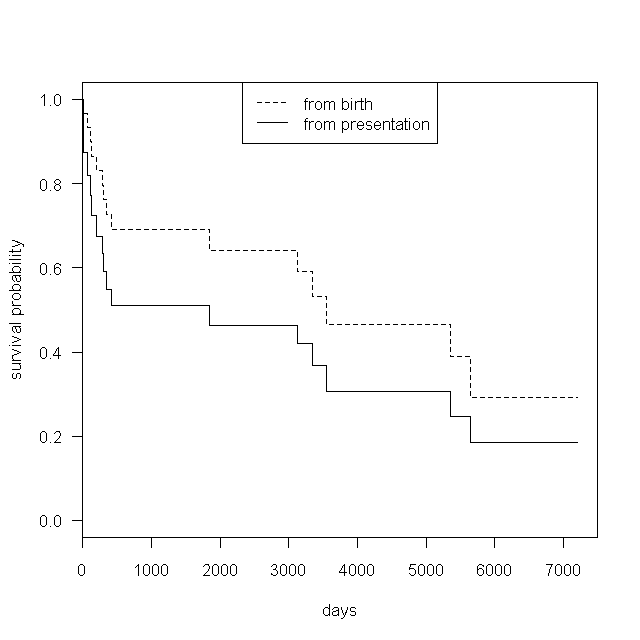
ノンパラメトリックなカプラン=マイヤ法は,データを使って直接生存曲線を描くもので,どんな生存曲線にも対応する。しかし,データによっては,何らかの仮定をおけば指数分布とかワイブル分布といった単純な分布を生存曲線に当てはめることが可能なことがある。ワイブル曲線を当てはめ,信頼区間付きで描画したのが図3である。パラメトリックな曲線の信頼区間は,ノンパラメトリックな曲線の信頼区間よりも一般に狭いが,この精度向上は,仮定を増やすことを代償として得られたものであり,バイアスを増やしてしまうことにつながるかもしれない。
固定時間間隔内でのイベントの単純な記述は,可能な説明変数の影響を調べる場合に容易に拡張できて,臨床的に,より役に立つようになる。
ランダム化試験では,すべての説明変数(リスク因子,共変量,予測因子あるいは独立変数としても知られている)が,ランダム化の時点において定義されていて,ランダム化という行為によって(偶然の変動を別にすれば)異なる治療群間でバランスがとれていることが保証されている。
ここで調べるのは,肺動脈の解剖学的所見(paanat)と来院時年齢が1歳未満かどうか(agepresx)の影響である。表5は,これらの死亡イベントへの影響を1つずつ別々にみた場合(左側の単変量解析と書かれている方)と,同時にみた場合(右側の多変量解析と書かれている方)をまとめたものである。
Rで実行するコードはtable5.Rである。
K-M(カプラン=マイヤ法)で推定された生存関数は,患者の2つのカテゴリについて容易に計算できることは明らかである。
表6と図6に肺動脈の解剖学的所見が異なる2群(paanat=0とpaanat=1)別々にK-Mで生存関数を推定した結果を示した。Rで書いたコード[table6figure6.R]を実行すると,表6を作るために必要な情報と下図が得られる(直接ファイル出力されるので注意)。
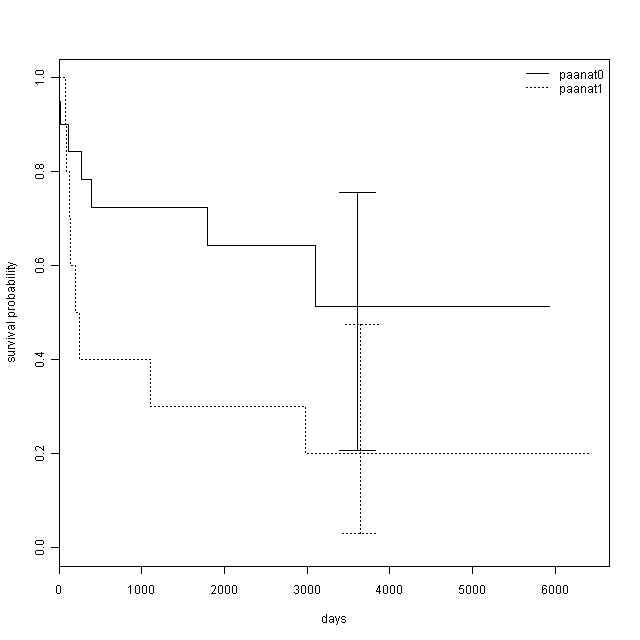
表6にはイベントが起こった瞬間のハザードと1年当たりのハザード及びその標準誤差(Cox and Oakesによる)が,2群別々に,1年未満と1〜10年までの2区間に分けて計算して示されている。例えばpaanat=0群について来院1年未満での死亡イベントが発生した時点でのリスク集合は20, 19, 16, 14人で,各1名ずつの死亡が起こっているので,
f <- c(1,1,1,1) r <- c(20,19,16,14) sum(f/r) sqrt(sum(f/(r*(r-f))))
選んだ時間の生存,例えば1年間の生存を比較することは,観察された生存の差とその推定された標準誤差に基づいて近似的なp値を計算することによって可能である。多くの他の目的のために,このような2群間での生存経験全体の比較は望ましいことである。そのためには,ログランク検定あるいはコックス=マンテル検定を要する。
表7にログランク検定の結果とハザード比が示されている。この検定を実行するためのRのコードはlogrank.Rだが,出力は以下のようになる。
Call:
survdiff(formula = Surv(followup, dead) ~ paanat, data = dat)
N Observed Expected (O-E)^2/E (O-E)^2/V
paanat=0 20 7 10.48 1.15 3.87
paanat=1 10 8 4.52 2.68 3.87
Chisq= 3.9 on 1 degrees of freedom, p= 0.0493
[1] 2.648137表7と微妙に異なる結果なのは丸め誤差であり,もちろんRの結果の方が正しい。
複数の説明変数の目的変数への影響を,互いに他の変数の影響を調整しながら求めるための多変量解析として,ロジスティック回帰分析が行われる。モデルは,
p/(1-p)=d0×d1×…×dIである。
モデルの両辺の対数をとって右辺を線型結合に直せば,係数は比較的容易に求められる。求めた係数は,対数オッズ比なので,指数をとってオッズ比に直す。結果は表8に示されている。
この結果を得るためのRのコードは,既に5.3.で示した通り,table5.Rである。ロジスティック回帰分析に該当する部分の出力は下記の通り。
(Intercept) paanat agepresx
0.3382121 6.9484700 0.3450070
2.5 % 97.5 %
(Intercept) 0.09415143 0.9765344
paanat 1.13747110 62.0705248
agepresx 0.02601249 2.9421095
Call:
glm(formula = dedlyrpp ~ paanat + agepresx, family = binomial,
data = dat2)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.5550 -0.7633 -0.7633 0.8421 1.6586
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.0841 0.5800 -1.869 0.0616 .
paanat 1.9385 0.9864 1.965 0.0494 *
agepresx -1.0642 1.1712 -0.909 0.3636
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 35.594 on 26 degrees of freedom
Residual deviance: 31.115 on 24 degrees of freedom
AIC: 37.115
Number of Fisher Scoring iterations: 4表8と若干数値が違うのは,ほぼ丸め誤差によると思われる。
比例ハザード性を仮定すれば,時点tにおけるハザード比は,
h(t) = h0(t)×h1×…×hiと表現できる。分析実行のためのRコードはtable9.Rであり,出力をまとめ直せば表9ができる。
(読者への警告:もしこれまでの節が難しく感じられたら,たぶん,いまが第11節の考察に飛ぶべきところだ!)とあったので,この勉強会で読むのはやめた。
Correspondence to: minato@phi.med.gunma-u.ac.jp.